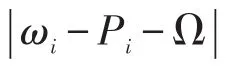考虑负荷的大规模DG系统的建模与同步稳定性

伍 娟，周 洪，余 昶

（武汉大学电气与自动化学院，武汉 430072）

靠近负荷端、可靠性高的、环境友好型的分布式发电DG（distributed generation）是电网研究领域的热点[1-3]。分布式发电可以降低输配电损耗，并有并网运行和孤岛运行两种模式，采用这种发电方式，大规模停电事故的发生频率能得到有效的降低，电网的安全性和可靠性可得到提高。如风能、太阳能等环保的可再生能源技术的发展推动了分布式发电技术的前进[4-5]。然而可再生能源能量密度较低，需要大规模采集才能有效利用。而目前部分对于分布式系统的研究中，其对象都是单个DG或较少数目的DG系统[6-7]。然而系统的DG节点数越多，系统的运行状况越复杂，传统的单个或有限多个DG的稳定性分析方法不适用于大规模分布式发电系统中。文献[3]对大规模分布式发电系统的稳定性进行了仿真分析，但其研究对象是均匀场网络。而根据实际情况来看，DG节点之间的耦合强度受到节点电压、线路阻抗、下垂系数等多个因素的影响，简单的假设耦合强度都相等显然有些不符合实际。现分布式发电装置与家庭用户结合起来构成产消者，因此本文在建立系统数学模型时考虑了节点负荷。

从目前的研究来看，Kuramoto模型是研究电网同步稳定问题的热点模型。分析Kuramoto模型的同步稳定性质的普遍途径是利用矩阵和Lyapunov函数等方法[8-9]。然而这些方法推导出的参数条件中往往含有矩阵的特征值，而大规模网络的矩阵较为复杂，因此该方法不太适用于大规模分布式发电系统的同步稳定性研究。应用梯度系统和Łojasiewicz不等式的相关知识可以改进研究结果，并且方便计算。文献[10]改进了文献[11-12]的结果，将频率同步的初始相位条件扩展到整个圆上。文献[13]通过梯度和Łojasiewicz不等式揭示了势与梯度之间的关系，解决电网的暂态稳定性问题。文献[14]通过Łojasiewicz不等式来说明系统的同步条件和同步速率。文献[15]基于梯度公式和能量计算来探讨电网的暂态稳定性问题，研究了非均匀Kuramoto模型的同步问题。然而目前将其运用到分布式发电系统中的相关研究较少。

不同于对单个DG或小规模DG系统的研究，本文的研究对象为非均匀场大规模分布式发电系统，在考虑节点负荷的情况下对系统的稳定性进行了研究。通过推导得到了系统在半圆上锁相的必要条件，并利用Łojasiewicz不等式证明系统达到平衡点的速度是指数的。通过3种网络拓扑的稳定过程的仿真来验证结论的有效性，并比较了3种网络拓扑的同步能力的优劣。最后根据仿真结果设计了一个微电网算例，并通过其仿真结果得到可通过调节系统参数来提高系统的同步程度的结论。

1 分布式发电系统网络结构

现有低压配电网接线网络中应用广泛的星形网络、树形网络以及环形网络3种结构[16-18]如图1所示。星形结构的特点是引出线发生故障时互不影响，供电可靠性高，但其使用开关设备和导线较多，用于设备容量大或负荷性质重要、潮湿及腐蚀性环境。树形网络采用的开关设备较少，比较经济，但干线故障时影响范围大，供电可靠性低，因此一般与星形网络混合应用，适用于机械加工车间、机修或工具车间[18]。环形网络的供电可靠性最高，并且电能损耗和电压损耗较小，适合对电能质量要求较高的用户[19-20]。

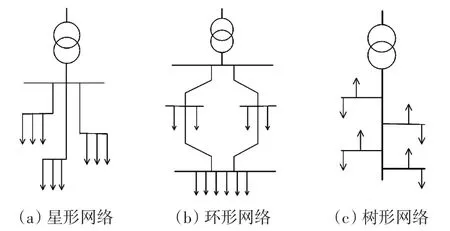
图1 低压配电网接线网络Fig.1 Wiring network of low-voltage distribution network

大规模DG并网可以基于现有配电网，无需进行多余改造，可降低成本。根据传统配电网的结构来构建大规模DG并入电网的结构，并考虑每个DG带有节点负荷，其拓扑如图2所示。

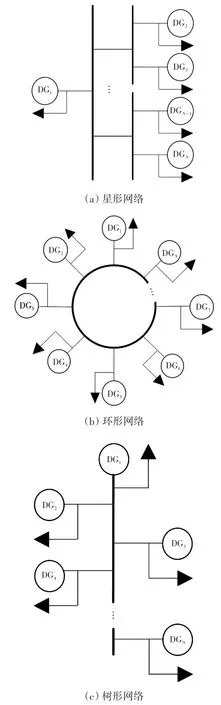
图2 带有节点负荷的分布式发电系统Fig.2 Distributed generation system with node load

2 分布式发电系统数学建模及分析

2.1 系统数学建模

对于一个含有N个节点耦合的网络，第i个节点发出的有功功率为

式中：Pi为第i个节点的有功功率；Ei为第i个节点的电压；Ej为第j个节点节点电压；Yij为第i个节点与第j个节点之间的导纳；θi和θj分别为第i个节点与第j个节点的相位。

对第i个节点采用f-P下垂控制，则有

式中：ωi为第i个节点的频率；ω0为无阻尼自然振荡角频率；ωθ为参考点的频率；Pθ为参考点的功率；mi为下垂系数。

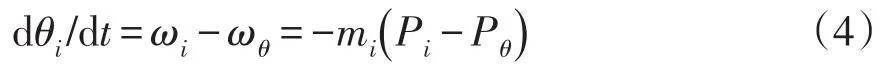
考虑每个DG节点带有负荷，那么上式改为

式中，Ploadi为第i个节点的负荷消耗的有功功率。

为了更具一般性，设节点负荷的阻抗值为

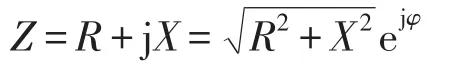
功率因数角为

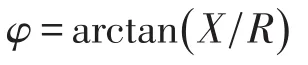
那么有如下推导过程。

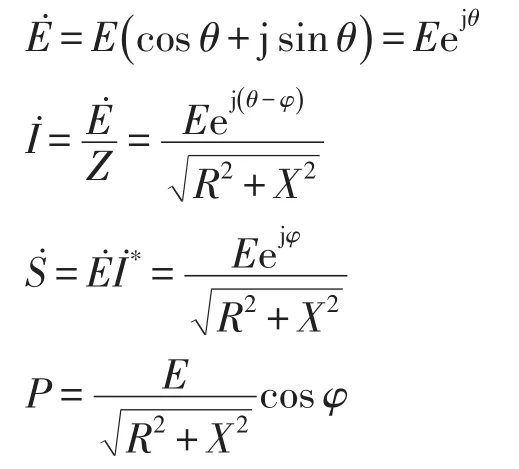
所以第i个节点的负荷消耗的有功功率为

综上可得带有负荷的节点的数学模型为

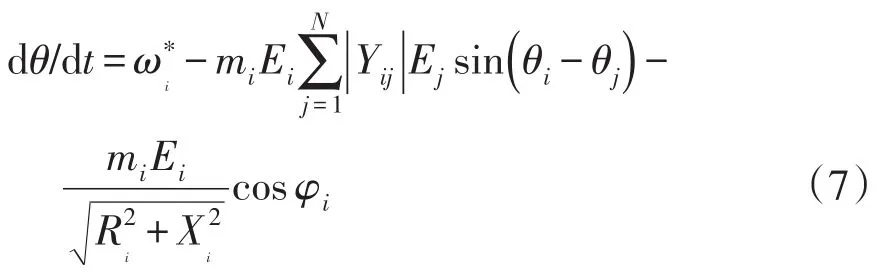
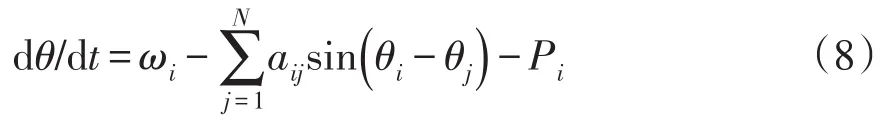
2.2 系统同步稳定性分析

本小节将对系统（8）的同步条件进行相关探究。首先对相关的同步定义以及使用的数学工具进行介绍。

2.2.1 同步概念及Łojasiewicz不等式

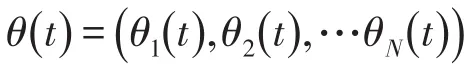
（1）称整个系统渐近达到锁相状态，若相对相位差收敛为某个常数，即

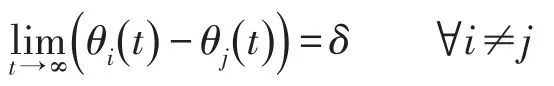
（2）称整个系统渐近达到相位同步状态，若相对相位差收敛为0，即

定义3.2[3，8]：为了描述整个系统的同步程度，定义序参量

式中，ψ为整个系统节点的平均相位。0≤r≤1，当r=0时，整个系统处于完全不同步状态；当r=1，所有节点的相位完全相同。因此可以根据r的大小来判断整个系统节点相位的同步程度。

2.2.2 同步稳定性分析

证明：对所有节点的瞬时频率求和可得

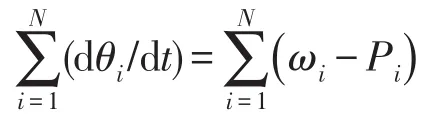
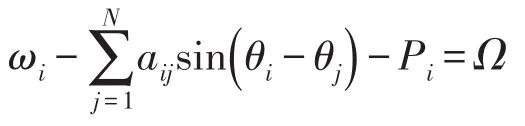
因此，系统达到锁相状态的必要条件为

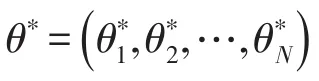
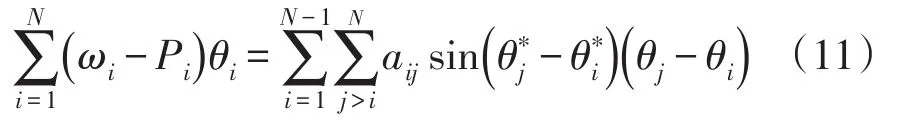
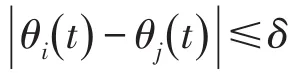
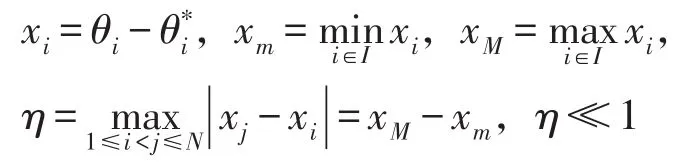
由引理3.7，可得到系统（8）的位势函数为

根据泰勒公式可得如下化简过程：

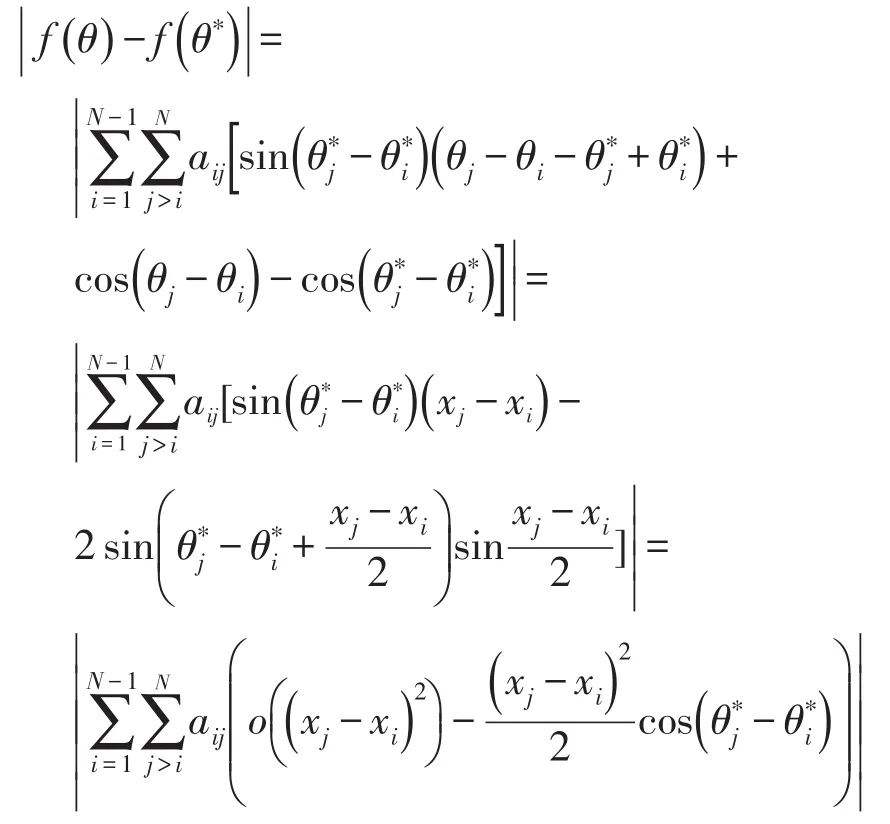
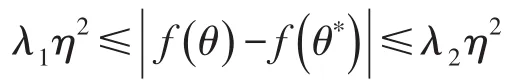
考虑 ∇f(θ)的无穷范数

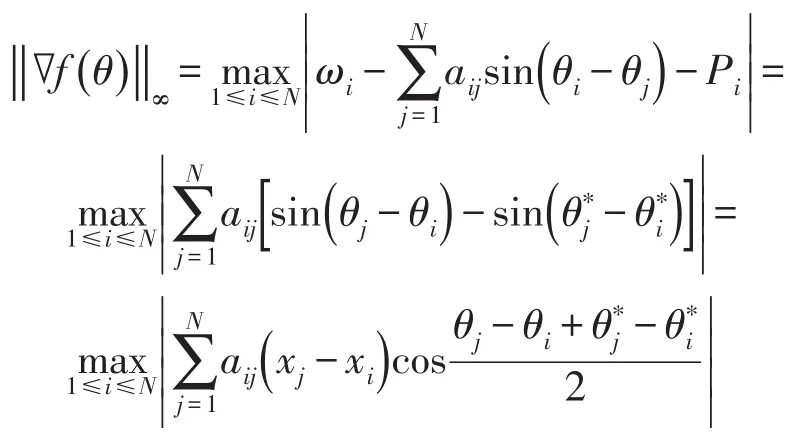
因为 ℵ(θ*)为θ*的足够小邻域，因此有

因此，存在常数0＜μ1＜μ2，使得下式成立：

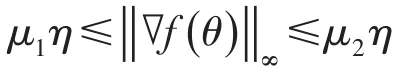
综上可得，

因此，系统（8）收敛到锁相状态的速率是指数的。

3 仿真分析

3.1 非均匀网络收敛为锁相状态

设网络节点数为200，并设所有节点的固有频率ωi是均值为0、在区间( )-0.1,0.1之间的随机分布，负荷的有功功率Pi是均值为0.1、在区间( )0,0.2之间的随机分布，那么Ω=-0.1。现考察两种情况下3种网络的稳定性。

情况1：设节点之间的耦合强度aij是初始值为0.3、差值为0.3的等差数列，即对于所有节点都满足条件（10）。

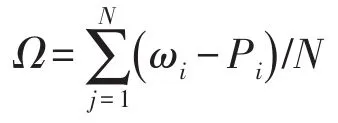
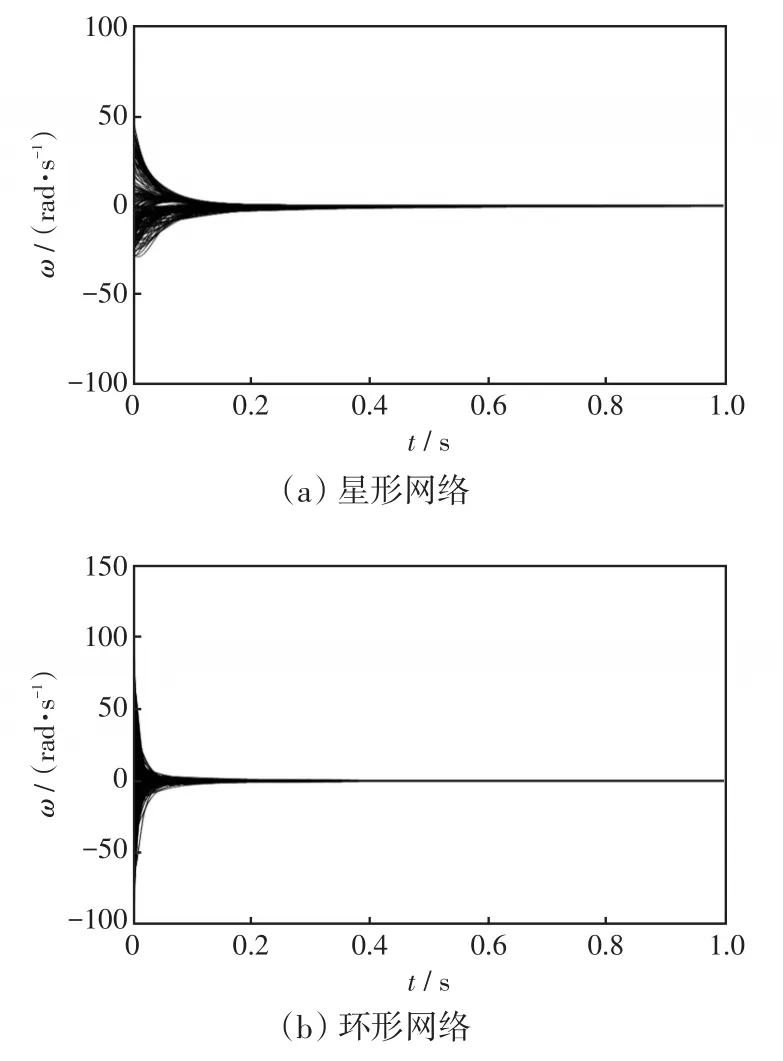
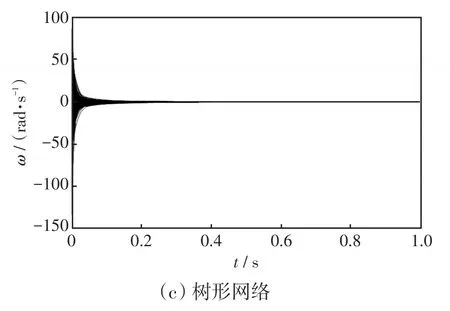
图3 情况1下3种网络的节点频率Fig.3 Node frequencies of three networks in Case 1

图4 情况2下3种网络的节点频率Fig.4 Node frequencies of three networks in Case 2

3.2 非均匀网络收敛为同步状态

依然设网络节点数为200，所有节点的固有频率ωi是均值为0、在区间( )-0.1，0.1之间的随机分布，每个节点的有功功率为Pi=ωi+0.1，节点之间的耦合强度aij呈幂律分布。3种网络节点的相位同步过程如图5所示。由图可知，经过不等时间的运动后，3种网络所有节点的相位会聚集到相同的位置，即达到相位同步状态，且频率会收敛到-0.1。结合4.1节和4.2节的仿真结果可知，系统所有节点的参数ωi-Pi都相等是系统能够达到相位同步的必要条件，且频率最终会收敛到ωi-Pi。本小节的仿真结果验证了推论3.6。

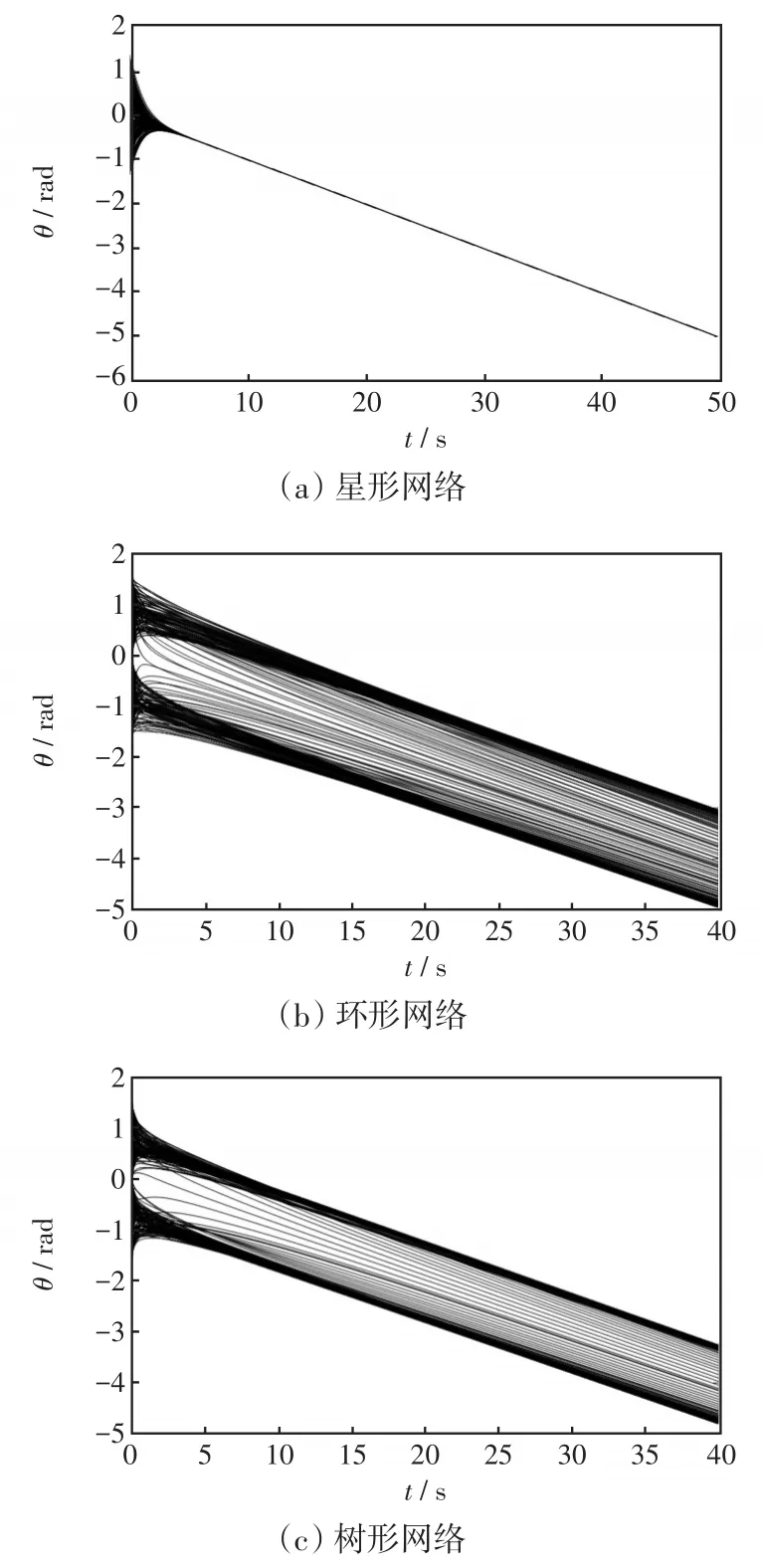
图5 相位稳定过程Fig.5 Phase stabilization process

3.3 3种网络同步稳定性比较

为了在相同的条件下对3种网络进行比较，现设所有节点的ωi-Pi=0，节点之间的耦合强度aij都相同，为了方便本小节设其为1。通过4.2节可知，在此参数条件下，3种网络经过不同的过渡时间都能达到相位同步，过渡时间也是网络结构在稳定速度方面的体现，因此将过渡时间也纳为稳定性比较的考察指标。不同规模的3种网络的序参量变化过程及过渡时间分别如图6及表1所示。

图6 序参量Fig.6 Order parameter

表1 不同规模下网络的过渡时间Tab.1 Transition time of networks at different scales

由图6和表1可知，网络规模的大小对星形网络的过渡时间影响不大，而环形网络与树形网络的过渡时间则随着节点数的增多而明显变长。并且从表1中可以看出，在相同的网络规模下，星形网络的过渡时间远远小于环形网络和树形网络，树形网络的过渡时间最长。

接下来探究在上述相同参数条件下，网络达到完全相位同步状态所需的临界耦合强度与网络规模的关系。为了使所有参数条件一致，取过渡时间为20 s，不同规模下网络达到完全相位同步所需的耦合强度如表2所示。星形网络的序参量受网络规模的影响不大，且相位完全同步所需的耦合强度与节点数无明显关系；而环形网络与树形网络所需耦合强度随节点数增多而增大。且在相同节点数时，星形网络的所需耦合强度最小，树形网络最大。

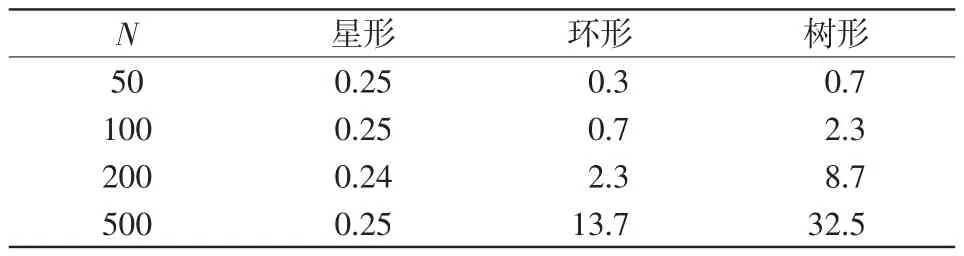
表2 序参量为1时耦合强度的值Tab.2 Value of coupling strength when the order parameter is 1

综上所述，星形网络需要较少的过渡时间达到相位稳定，所需的临界耦合强度也较小，并且稳定性不受网络规模的影响，因此为3种网络中的最优网络。而树形网络的过渡时间以及临界耦合强度较其他两种网络而言都较大，因此树形网络的同步稳定性是最差的。

4 算例分析

通过前面的仿真，可知在相同的参数情况下，星形网络的同步稳定性是3种网络中最优的一种。综合考虑经济因素与系统安全性，本文给出了如下一种星形与树形结合的低压微电网系统，其结构及相应数据如图7所示。设节点处的电压值均为220 V，下垂系数为10-5。不同线型有不同的阻抗值，那么根据系统参数及系统拓扑结构，各相邻节点之间共有4种不同的线路导纳值，这4种节点之间导纳值及耦合强度的计算结果如表3所示。设负荷的有功功率Pi是均值为0.1、在区间(0 ,0.2)之间的随机分布，ωi是均值为0、在区间(- 0.1,0.1)之间的随机分布，所有节点都满足条件（10）。该系统的频率及相位变化过程如图8所示。系统收敛为锁相状态，该结果再次验证了定理3.5。

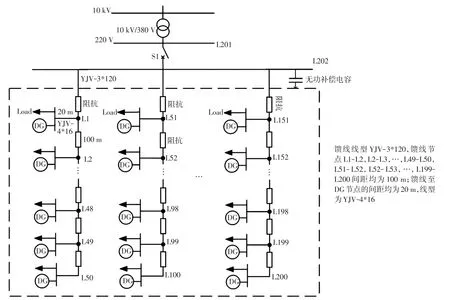
图7 低压微电网算例Fig.7 Example of low-voltage microgrid

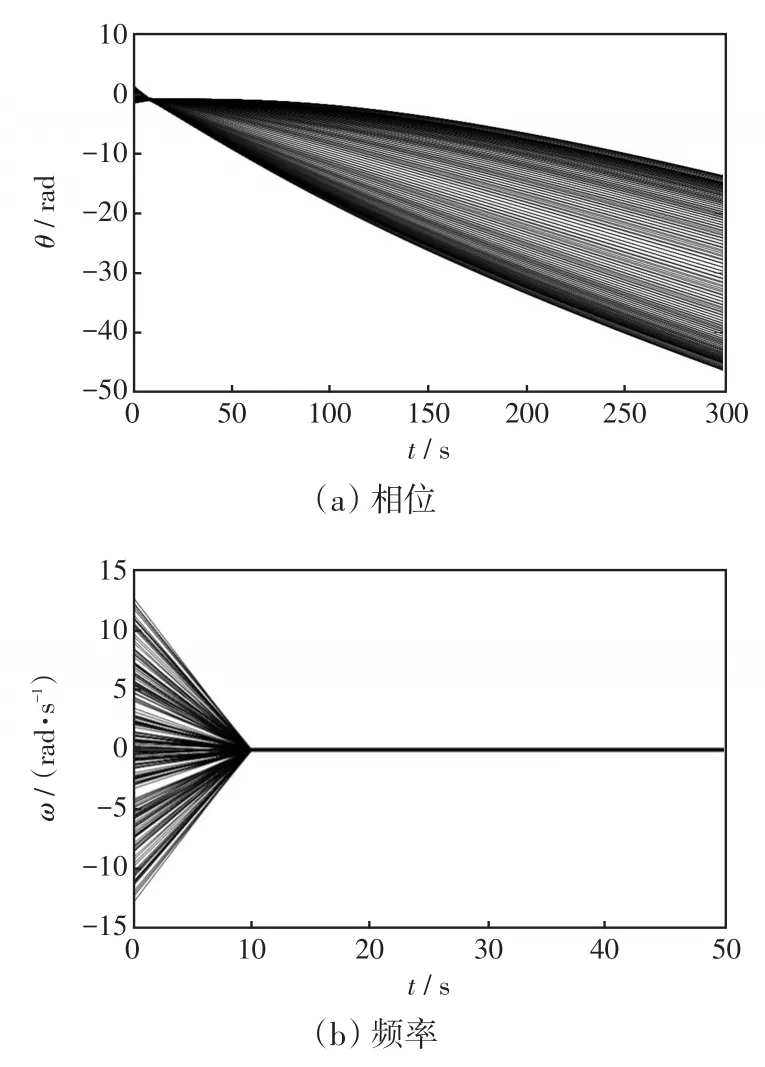
图8 系统的参量变化过程Fig.8 Changing process of system parameters

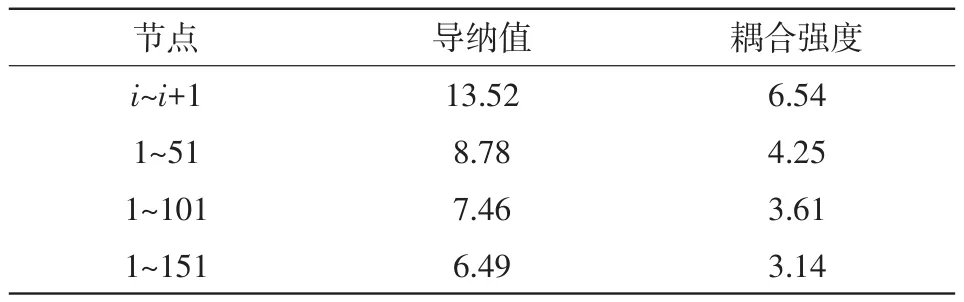
表3 节点间的阻抗值及耦合强度Tab.3 Impedance and coupling strength values between two nodes

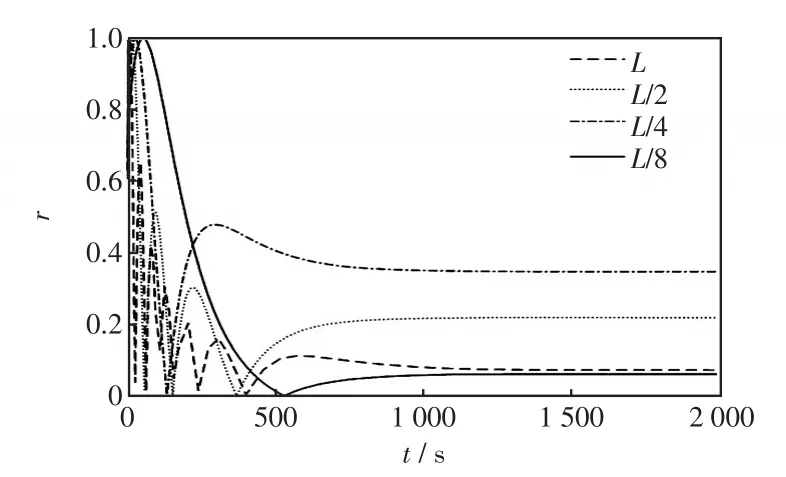
图9 算例序参量Fig.9 Order parameter of the example

5 结语

本文主要研究了带有节点负荷的大规模非均匀分布式发电系统的同步稳定性。介绍了低压配电网的3种网络拓扑结构及其优缺点，并由其得到带有节点负荷的分布式发电系统的网络拓扑结构。通过数学推导，得到系统频率在半圆内达到锁相状态的必要条件，并利用梯度系统和Łojasiewicz不等式的相关知识得到系统频率在1/4圆内时达到平衡点的速率是指数的。

对具有的相同耦合强度分布的3种网络进行了频率、相位以及序参量方面的比较与分析。根据仿真结果，在相同的条件下，星形网络的过渡时间以及进入完全相位同步所需的临界耦合强度都比环形网络、树形网络小，星形网络具有更优的同步稳定性。因此建议实际构建大规模分布式发电系统时可优先考虑星形网络。