采用谐波特性的电力负荷分类

张琦兵，张佳彬，樊陈，金哲倩，史锐，徐春雷

1. 国网江苏省电力有限公司，江苏 南京 210024

2. 河海大学 能源与电气学院，江苏 南京 211100

3. 中国电力科学研究院有限公司，江苏 南京 210003

电网仿真计算有赖于准确的负荷模型，可见其对电网规划调度以及运行分析、需求侧管理以及电价制定等方面都具有重要的作用[1]。随着智能电网建设的推进，电力电子化负荷设备的应用越来越广泛，电力负荷的电力电子化已成为一种必然趋势。负荷设备的电力电子化使得负荷特性变得更为复杂，相应的其非线性、随机性、多变性都会影响负荷建模结果的精确性以及适用性。随着电力电子类负荷接入电网的占比越来越高，给电力负荷模型及电网仿真带来较大的偏差[2−3]。因此对电力电子负荷设备占比越来越高的电网节点综合负荷的构成成分展开分析具有重要意义。

电力电子负荷设备的一个重要特征是具有较明显的端口谐波与间谐波[4−5]，呈现出明显的宽频域特性，如可出现与工频不同步的间谐波以及大于2 kHz的超高次谐波[6]。不同类型的电力电子设备具有不同的端口机电特性与谐波特性，但具有较高的相关性。因此，如何利用端口谐波、间谐波特性对综合负荷的构成成分进行分析值得深入研究。

传统负荷分类中大多数是通过行业进行负荷种类划分[7]，对于各负荷的输出特性划分较为有限，对于新型负荷的观测较少，可能导致行业内部分类不够清晰[8]。文献[9]按照行业不同的分类标准，同时考虑到了季节因素对负荷进行划分，虽然提高了划分的精确度，但是仍旧存在行业内部分类不够清晰的问题，尤其是对可调性强的电力电子设备。对于负荷划分的特征选取较多的是时域上的日负荷输出曲线，而对于频域上的特性关注较少。文献[10]根据日负荷曲线进行负荷分类，较好地解决了传统方法中局部最优问题，但是对于波动较大、规律性不强以及变化趋势不确定的数据处理能力较差。文献[11]将频域引入到负荷分类中，有效地区分出了不同周期分量，突出了电力负荷的峰谷波动特性，通过频域角度针对负荷进行分类是有意义的。

鉴于电力电子设备的多样性，本文提出了一种根据其端口谐波特性进行构成分析与分类的方法。针对电网中的典型负荷，通过其输出电流的仿真与分析，构建了初始的负荷分类。在此基础上，针对混合电流进行FCM聚类，并分析负荷的构成与分类的合理性。

1 谐波信号的分析

快速傅立叶变换(fast fourier transform，FFT)是谐波分析的主要方法之一，具有易于实现、实用性强的特点，但会存在栅栏效应和频谱泄露的问题[12]。

以式(1)的信号为例，使用FFT做谐波分析，结果如图1所示。

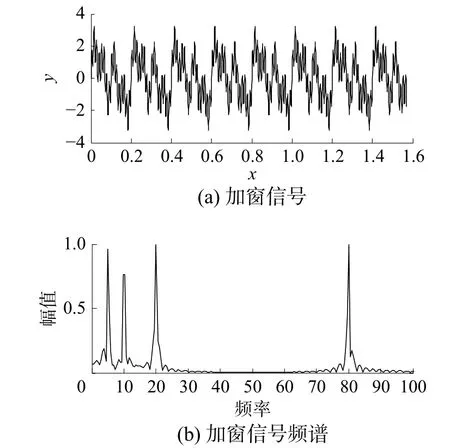
图1 FFT分析频谱

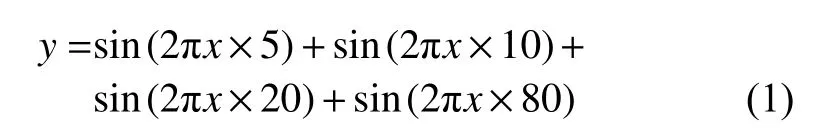
由图1可以看出栅栏效应和频谱泄露现象明显，这会使得结果偏差较大。因此引入公式(2)的具有较快旁瓣衰减速度的Hanning窗函数以减小误差，使用加窗FFT做谐波分析，结果如图2所示。

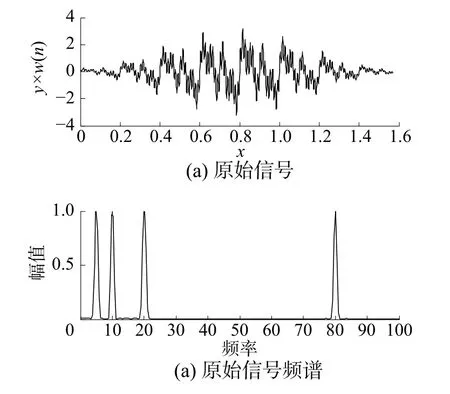
图2 基于Hanning窗的FFT分析频谱图

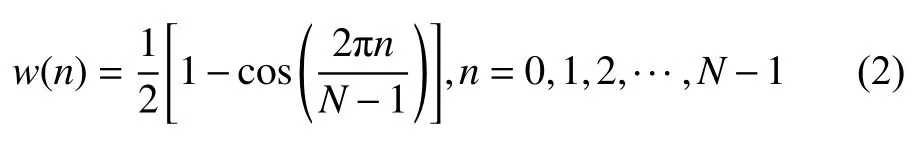
由图2可见，使用加窗FFT有效改善了谐波分析中主瓣与旁瓣分析的准确性，对于周期稳定的信号具有较好的谐波分析能力。

鉴于分析建立的模型是三相对称的，所以输出信号也是三相对称的，为了简化研究，着重对A相输出电流进行分析。现有的电能表在一定范围内能测量出基波及畸变分量，但随着测量频率的增加，测量所产生的偏差逐渐变大，由于高频分量在公共端的含量较小，所以在分析中可不考虑频率过高的分量，因此在研究中选择的频率为0～2 500 Hz。同时，为了减少基波分量过大的影响，放大对非基波分量的考虑，将用于分析频域数据中的基波分量设置为零。

2 负荷谐波特性分析

2.1 传统负荷谐波特性分析

针对传统负荷，以配电网中典型负荷—变压器、电动机和三相交流电弧炉为例。其中，在正常配电网运行情况下，变压器处于不饱和运行状态。对典型传统负荷建立相应的仿真模型得到输出电流的频谱，如图3所示。

由图3可见，变压器与电动机的特性较为相近，不存在电流畸变，只含有极少量的直流分量。三相交流电弧炉输出电流较大，且以奇次谐波分量为主，随着谐波次数增加而减少，还存在少量的直流分量以及偶次谐波分量。

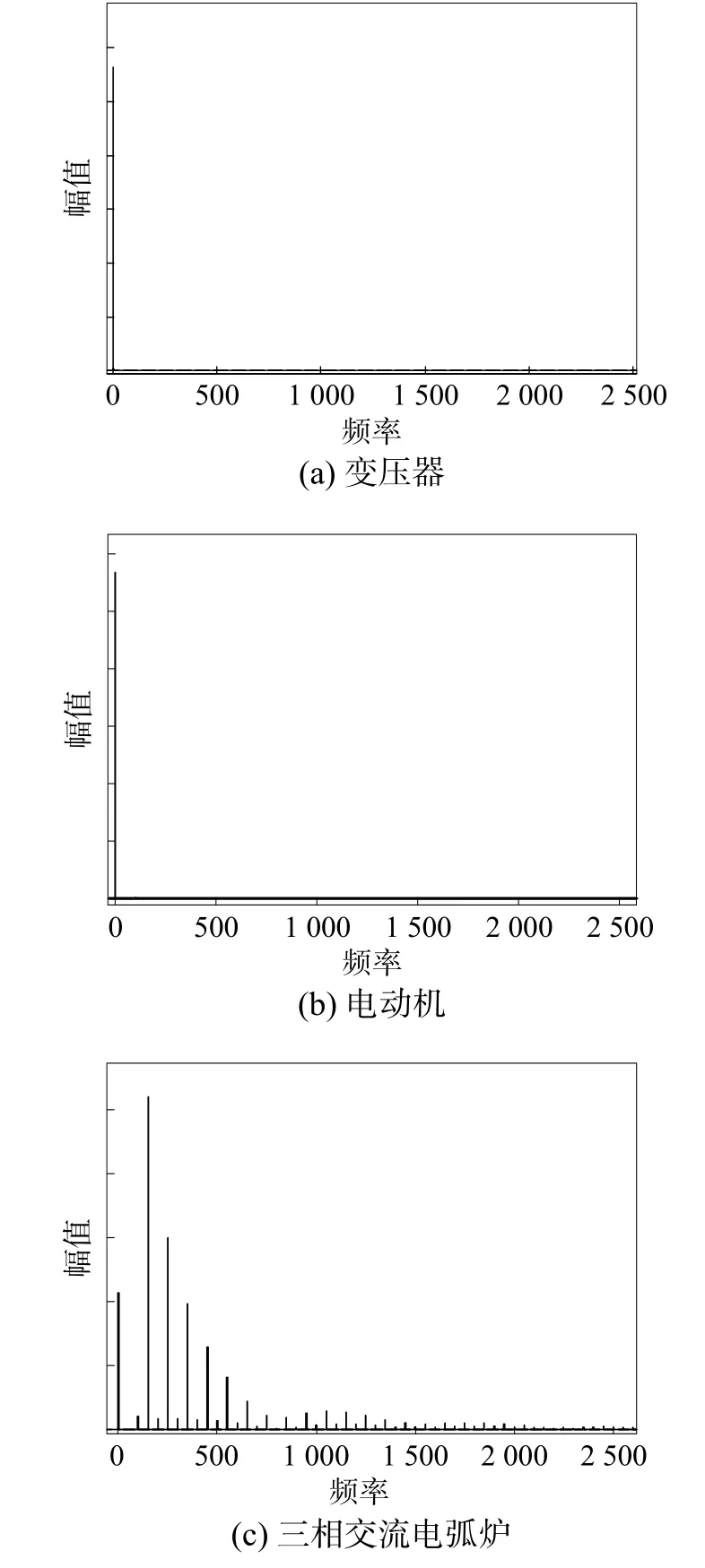
图3 典型传统负荷输出电流频谱

2.2 电力电子负荷谐波分析

针对电力电子负荷，以配电网中典型负荷—多脉冲整流器、基于SVPWM整流器和光伏系统为例，建立相应的仿真模型得到输出电流的频谱[13−14]，如图4所示。其中多脉冲整流器选用六脉冲整流器及十二脉冲整流器。

由图4可见，多脉冲整流器主要以特征谐波分量为主，特征谐波分量随着谐波次数的增加而减少。基于SVPWM整流器及光伏系统的电流中成分较为复杂，存在明显的间谐波、偶次谐波以及高频次谐波(主要集中在开关频率附近)。

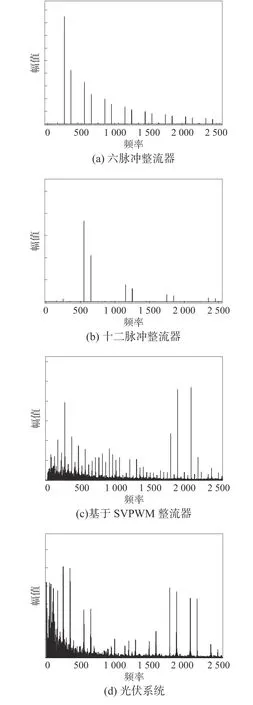
图4 电力电子负荷输出电流频谱图

2.3 其他典型设备的谐波分析

非线性负荷的谐波、间谐波在影响电能质量的同时，也会引起谐波源之间产生谐振。以六脉冲整流器为例，当输入到六脉冲整流器的电压源不是正弦波时，会存在一个幅值较小的非工频分量，其输出电流频谱图如图5所示。

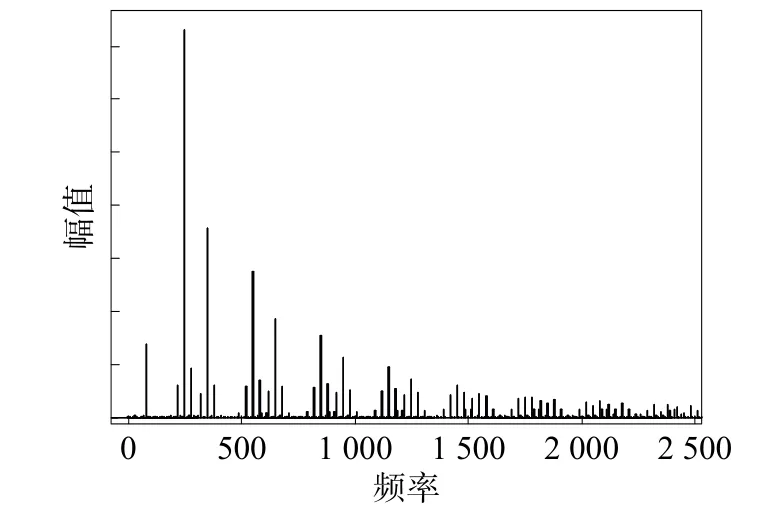
图5 输入畸变情况下的六脉冲整流器输出电流频谱

由图5可见，当输入信号为非正弦信号时，会增大电流的畸变程度，产生除原有特征谐波分量外的间谐波分量及其他次谐波分量。但原来的特征谐波分量仍呈现出衰减的趋势，并依旧为主要分量。

实际上，谐波也会对正常工作下的变压器、电动机产生影响，通过对变压器与基于SVPWM的整流器并联以后的公共连接点(Point of Common Coupling，PCC)输出的电流频谱图展开分析，结果如图6所示。

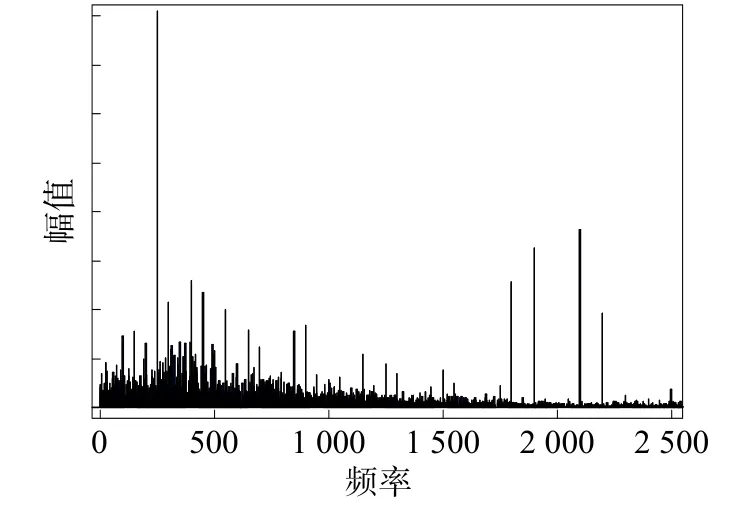
图6 变压器与基于SVPWM整流器并联输出电流频谱

基于SVPWM的整流器与变压器并联工作的输出电流中，5次谐波分量所占的比重明显增加，并且5次谐波附近的奇次谐波电流所占的比重也变大，但增加幅度相比5次谐波的增加幅度较小。这种情况可能是由于在变压器端出现谐振造成的，再针对电动机分析后发现其具有类似的特性。

3 谐波的初始分类

将样本硬性划分的极端情况发生，考虑到了数据的模糊性，模糊C均值算法实质上是一种寻找目标函数最小最优的算法，其具体流程如图7所示[15−16]。

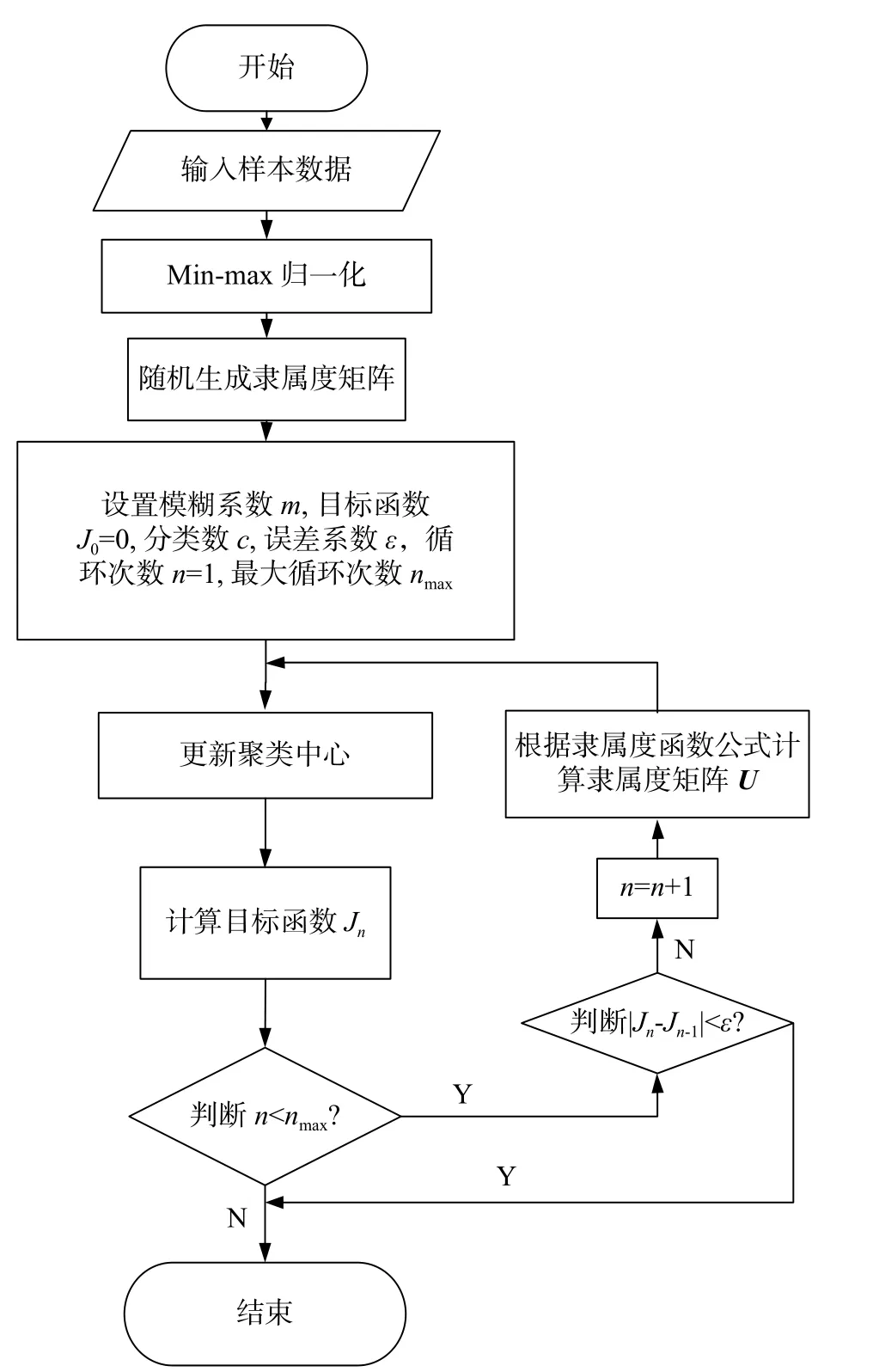
图7 FCM算法流程图

针对以上对于各负荷的谐波特性分析，可将负荷分为以下3类。

A类负荷特点：直流分量较大，其他频率上的电流分量较小，可能在5次谐波及其附近存在较少的谐波分量，几乎不存在间谐波分量，代表负荷有变压器、电动机。

B类负荷特点：特征谐波分量随谐波次数增加而减少，存在较少的间谐波分量，直流分量也相对较小，代表负荷有多脉冲整流器、三相电弧炉。

C类负荷特点：间谐波分量较大，在低次频率范围内含有较多的谐波，在开关频率附近也存在较大的高频次谐波分量，呈现出多峰的频谱图，代表负荷有含控制环节的整流器、光伏系统。

4 基于模糊C均值的负荷分类研究

4.1 模糊C均值算法

模糊C均值(fuzzy C-means，FCM)算法是将模糊概念结合到传统聚类方法中。该算法避免了

模糊C均值算法需要满足的约束条件是

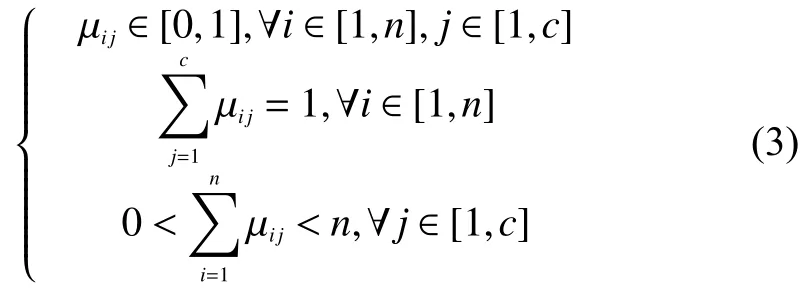
目标函数表达式为

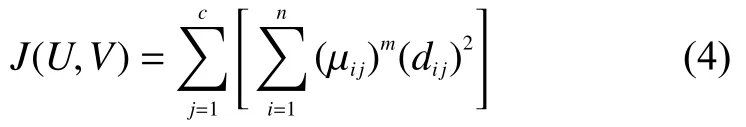
隶属度计算函数

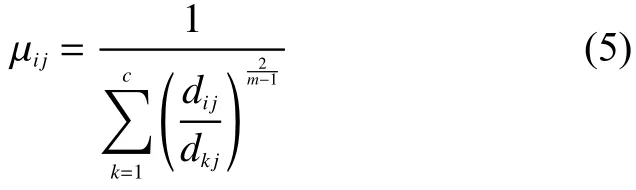
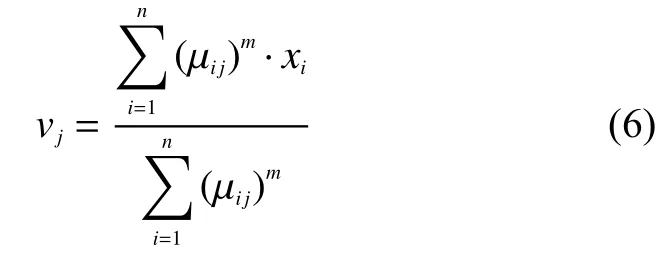
聚类中心更新公式式中：设数据集X={x1,x2,…,xn}，n为数据集的样本总数，xi(i=1,2,…,n)为第i个样本，c为聚类类别数(2≤c≤n)，类中心数据集V={v1,v2,…,vc}，vj(j=1,2,…,c)为第j个聚类中心，模糊加权指数m，隶属度矩阵U，µij为样本xi属于类中心vj的隶属度，dij为样本xi到类中心vj的距离。

4.2 典型负荷特性

通过以上分析可知，负荷大体分为3类，其特征明显且易于区分，所以此处设置聚类类别数c为3。

将前面几种负荷并联并建立仿真模型，提取270组输出电流数据作为分析对象。将该数据经过基于Hanning窗的FFT，得到频域数据，并将工频分量的幅值置零，即为负荷分析所需的样本[17]。

本文采用多次试验对比确定模糊加权系数m。已知模糊加权系数的取值范围为1.5～3，因此本文以0.1为跨度，1.5为起始模糊加权系数进行多次聚类，选择聚类结果最为清晰的模糊加权系数[18]，最终得到的模糊加权系数为1.8。

初始化模糊系数m、目标函数J0、分类数c、误差系数ε、循环次数n以及最大循环次数nmax后，随机生成满足约束条件(3)的隶属度矩阵，根据随机生成的隶属度矩阵通过式(6)计算对应的聚类中心值，并作为初始聚类中心，根据聚类中心以及隶属度矩阵通过式(4)计算对应的目标函数值，将|Jn−Jn−1| 与允许误差系数ε做对比，当比允许误差系数ε更大，并且循环次数n小于最大循环次数nmax，更新循环次数n=n+1，并且根据聚类中心通过式(5)计算隶属度矩阵，再根据新的隶属度矩阵通过式(6)更新聚类中心进行循环计算；当比允许误差系数ε相对小或者循环次数大于或等于最大循环次数nmax时，算法结束，输出聚类结果(聚类中心以及隶属度矩阵)。

图8为聚类中心特征图，聚类出的3类特征与初步分类的3类负荷特点相对应。第1类负荷对应A类负荷，非工频分量以直流分量为主，含有少量的以5次谐波为主要谐波分量，间谐波分量极少，主要是电动机、变压器等负荷；第2类负荷对应B类负荷，特征谐波随着谐波次数的增加呈减少的趋势，间谐波含量相对较少，主要是三相交流电弧炉、多脉冲整流器等负荷；第3类负荷对应C类负荷，在高频部分出现明显的谐波分量，间谐波含量明显比前面2种大，主要以含控制环节的整流器、光伏系统等负荷为主。由此可见，聚类中心能表达出各类的负荷特征，可作为各类的典型负荷特性。

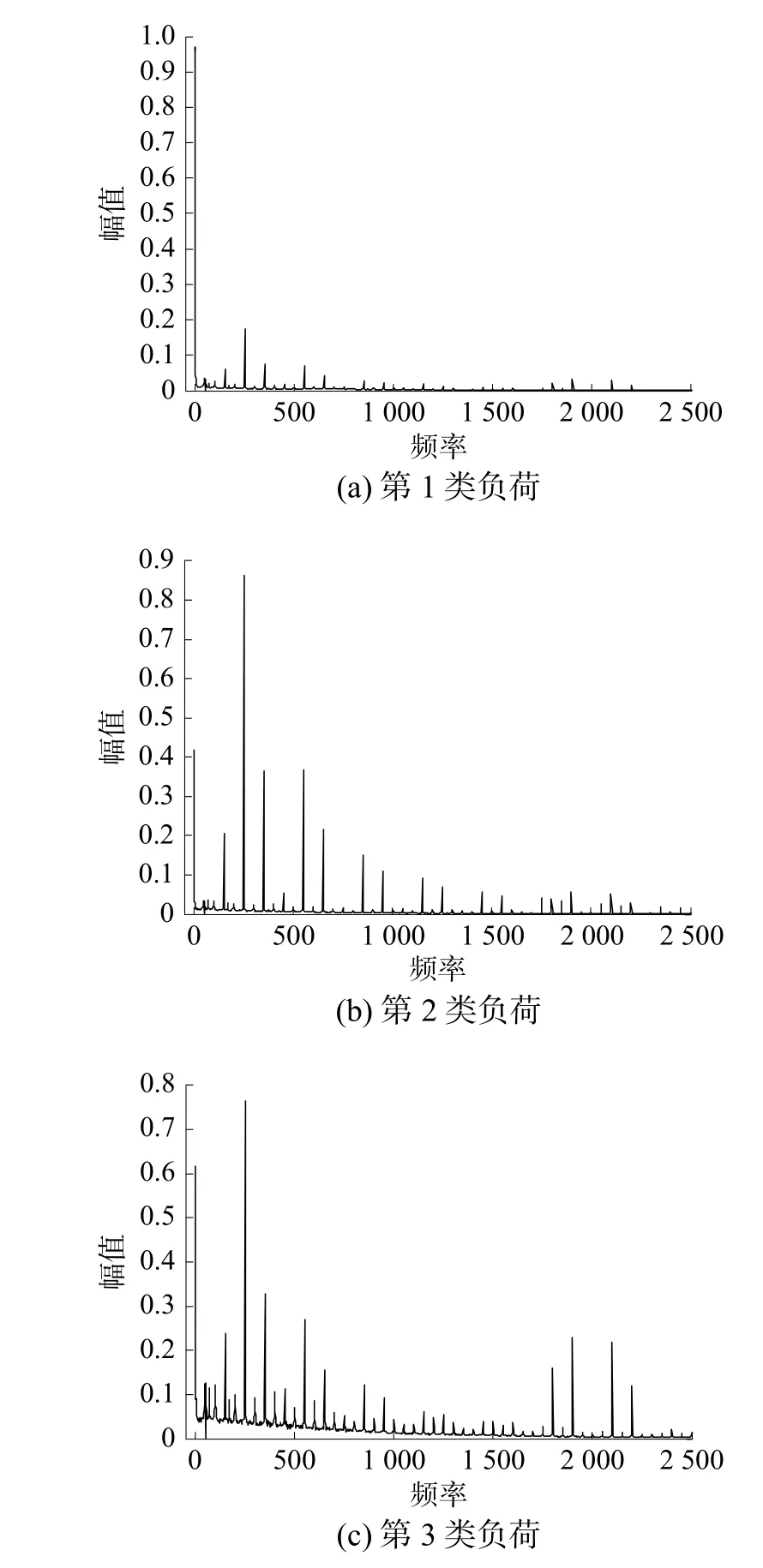
图8 聚类中心特征

为了验证聚类结果的典型性，在原有的270组数据的基础之上加入新的100组数据，对该370组样本集进行重新聚类，得到新的负荷数据矩阵。将新得到的负荷数据矩阵与原始数据得到的负荷数据矩阵做对比，两者的均方差如表1所示。

表1 新旧典型负荷对比

表1中的均方差可以看出两者差异很小，这主要是由于聚类过程产生的偏差以及谐波源之间相互影响产生的偏差，因此可以证明聚类的典型负荷特性具有代表性。

4.3 负荷含有率情况表达

图9与表2分别为随机选取一组数据样本，其除去基波的频谱图与经过聚类得到的隶属度矩阵。

从图9可以看出，混合负荷具有明显的直流分量、5次谐波分量，较多的高次谐波分量以及相对较多的间谐波分量；该混合负荷中第1类负荷与第3类负荷所占的比重最多。从表2可以看出，对应的隶属度反映出混合负荷的第1类负荷含有率最高，其次是第3类负荷，与频谱图分析相对应，表明隶属度能够在一定程度上反应负荷构成情况。

表2 样本例子隶属度

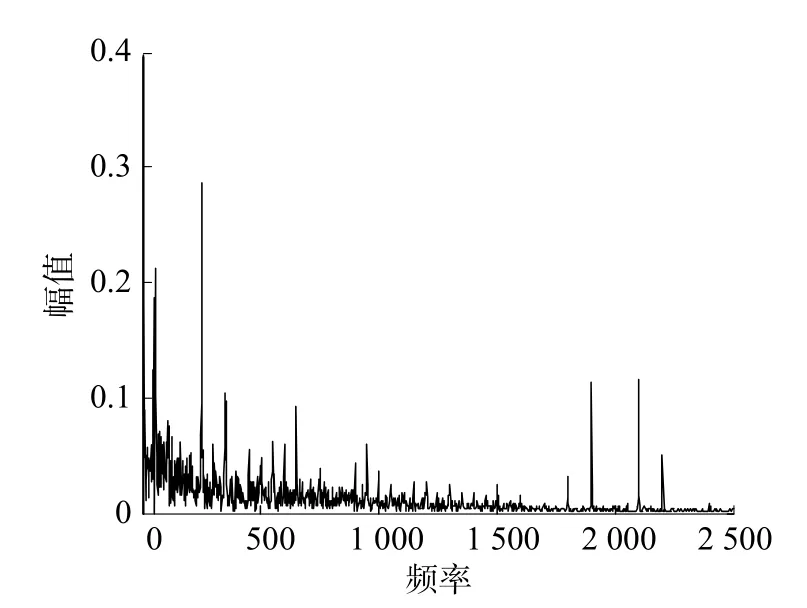
图9 混合负荷输出电流频谱图

为了验证负荷含有率与隶属度之间的关系，排除偶然性，下面对多组数据进行对比分析。

从原始采样数据中随机选取100组输出电流时域数据及其对应的隶属度，使用图10的负荷含 有率的验证流程图进行验证，结果如下。

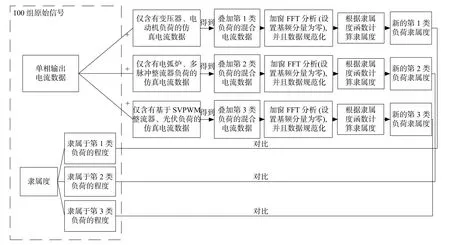
图10 负荷含有率表达情况验证流程图

1)第1类负荷

将第1类负荷输出电流叠加前后的隶属度做对比，结果其中100组数据中有20组数据的第1类负荷隶属度出现略微下降，而80组数据出现不同程度的上升。图11为第1类负荷隶属度叠加前后的变化情况，表3是20组第1类负荷隶属度下降的情况。

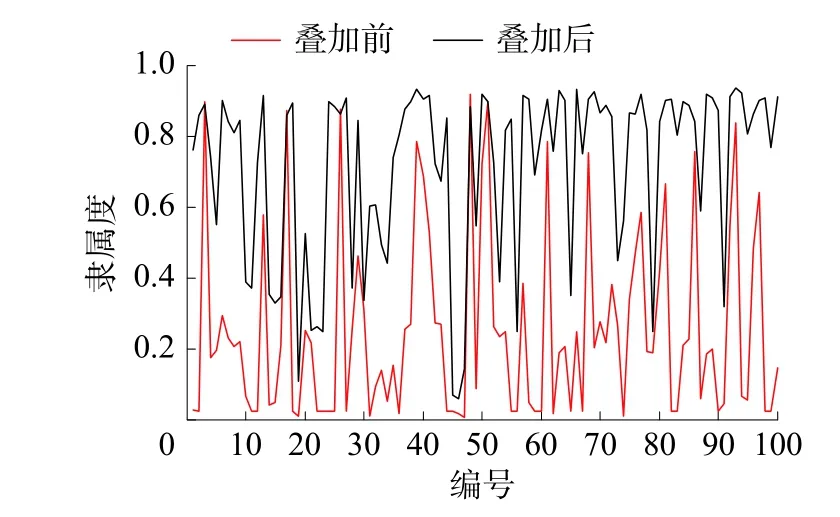
图11 第1类负荷叠加前后第1类隶属度对比

从 11图及表3的情况可以看出，出现隶属度下降的20组数据的隶属度在叠加之前就很大，而叠加后出现了略微的下降，这可能是由于计算造成的误差以及受到聚类结果的影响。整体来说，叠加前后隶属度数据变化情况与输出电流叠加上第1类负荷后，第1类负荷成分占比应增加的趋势一致，这表明隶属度能在一定程度上可以反映第1类负荷的含有率。

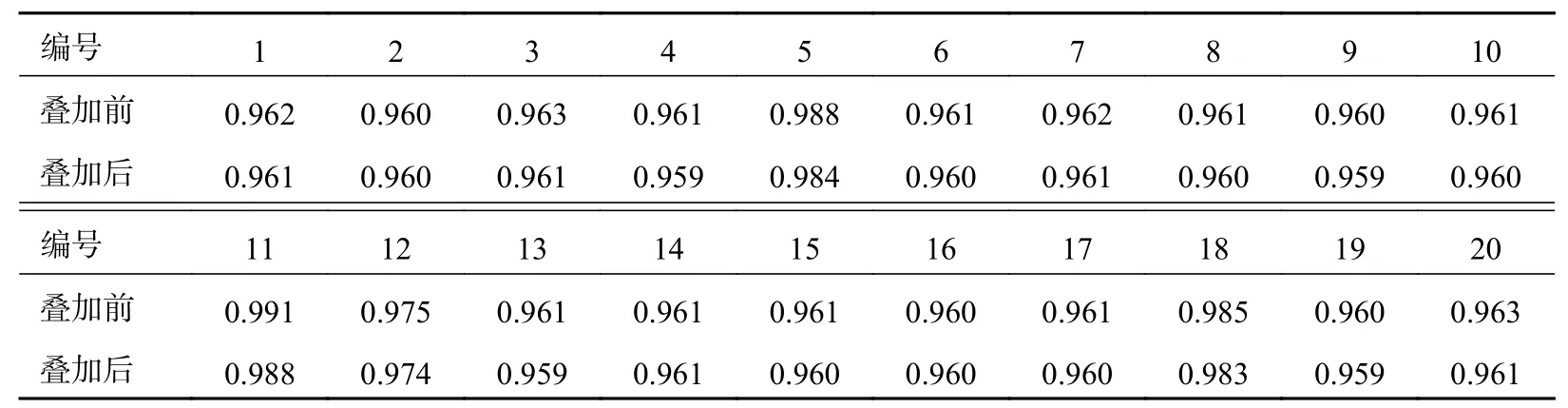
表3 第1类负荷隶属度下降的情况反映表

2)第2类负荷

将第2类负荷输出电流叠加前后的隶属度做对比，结果其中100组数据中有4组数据的第2类负荷隶属度出现略微下降，而96组数据出现不同程度的上升。图12为第2类负荷隶属度叠加前后的变化情况，表4为4组隶属度下降的情况。

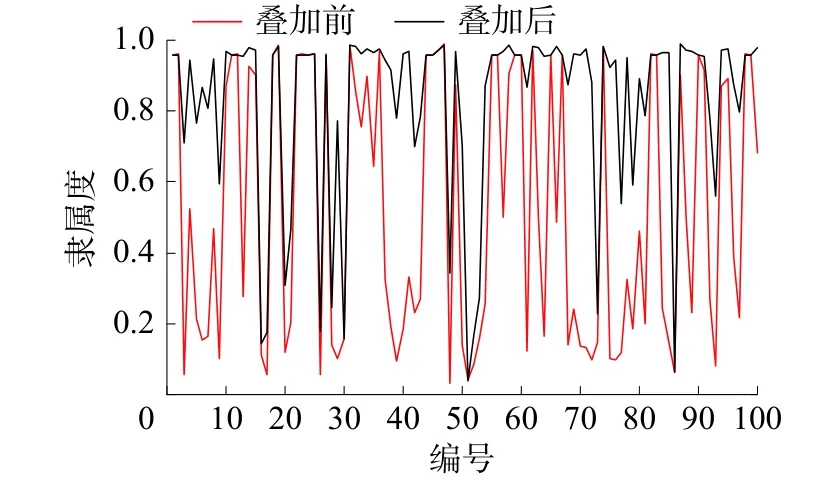
图12 第2类负荷叠加前后第2类隶属度对比

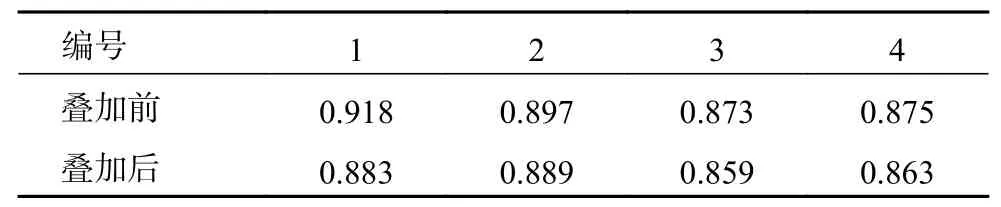
表4 第2类负荷隶属度下降的情况反映表

从图12及表4可以看出，出现隶属度下降的4组数据的隶属度在叠加之前就很大，而叠加后出现了略微的下降，这可能是由于计算造成的误差以及受到聚类结果的影响。整体来说，叠加前后隶属度数据变化情况与输出电流叠加上第2类负荷后第2类负荷成分占比应增加的趋势一致，这表明隶属度能在一定程度上可以反映第2类负荷的含有率。

3)第3类负荷

将第3类负荷输出电流的叠加前后隶属度做对比，结果其中100组数据中有6组数据的第3类负荷隶属度出现略微下降，而94组数据出现不同程度的上升。图13为第3类负荷隶属度叠加前后的变化情况，表5为6组第3类负荷隶属度下降的情况。

从图13及表5可以看出，出现隶属度下降的6组数据的隶属度在叠加之前就很大，而叠加后出现了略微的下降，这可能是由于计算造成的误差以及受到聚类结果的影响。整体来说，叠加前后隶属度数据变化情况与输出电流叠加上第3类负荷后第3类负荷成分占比应增加的趋势一致，这表明隶属度能在一定程度上可以反映第3类负荷的含有率。

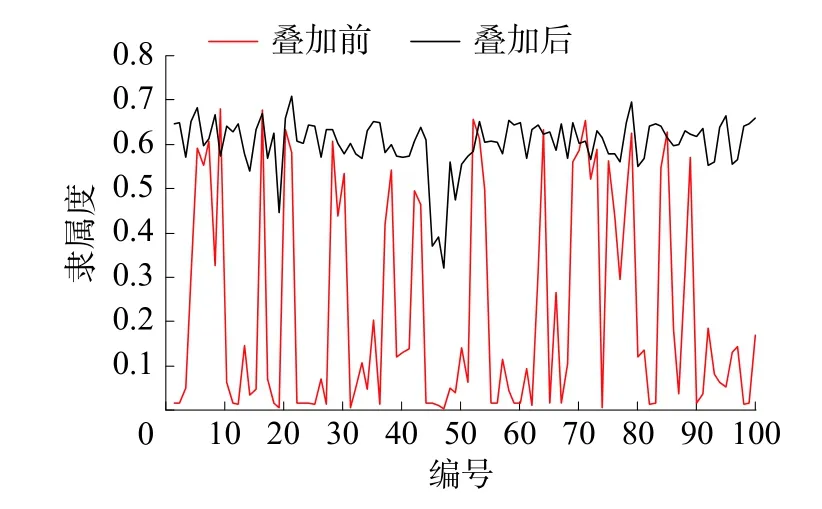
图13 第3类负荷叠加前后第3类隶属度对比

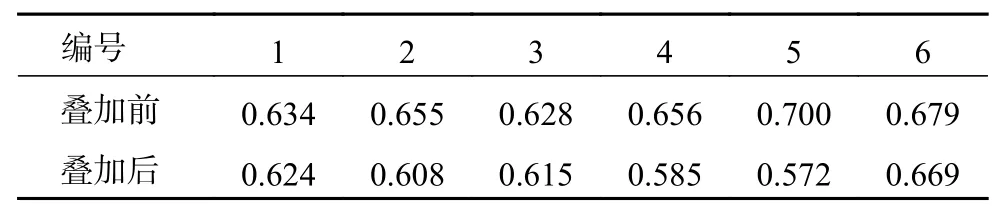
表5 第3类负荷隶属度下降的情况反映表

综上分析了隶属度反应负荷的含有率情况。图14为模糊C均值聚类结果与负荷成分分析对应关系图。本方法适用进一步对谐波模拟数据集的分析，验证了电力电子负荷构成成分分析及分类的合理性与有效性。

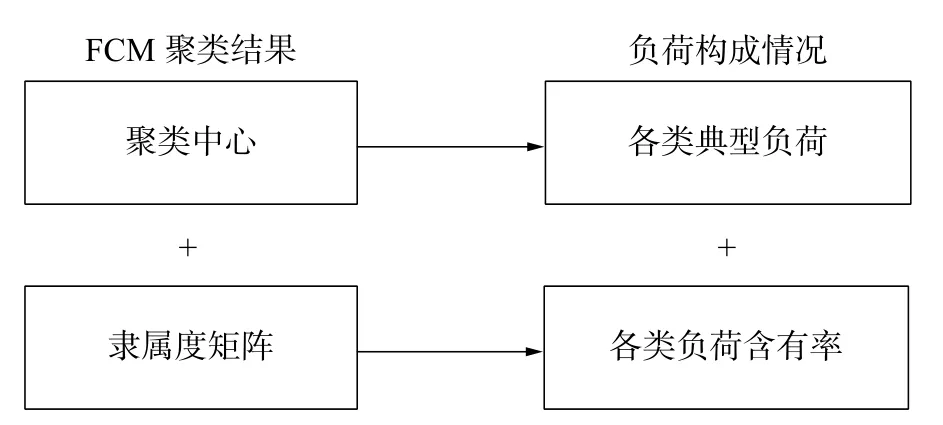
图14 聚类结果与负荷构成关系示意

5 结论

本文基于详细仿真模型分析了配电网中典型负荷的谐波特性，并对配电网的用电设备做出初步分类。引入模糊C均值算法用以分析负荷成分构成，验证了将负荷分为三大类的合理性。各分类的含有率可以通过隶属度矩阵来反映，即隶属度能够在一定程度上反映出混合负荷构成情况。

该方法最大的特点是对于混合负荷的成分构成展开分析，有利于了解负荷端情况，从而对负荷模型进行校正。由于采用的负荷种类以及工作场景仍不足，后续仍需在实际工程中加以验证。