二次样本筛选的高光谱图像分类研究

崔颖，王铃秀，李文山

1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

2.先进船舶通信与信息技术工业和信息化部重点实验室，黑龙江 哈尔滨 150001

对于高光谱分类来说，获取标记样本是非常困难的，主动学习的提出缓解了这一问题。近年来，主动学习在声音事件检测[1]、视觉情感分析[2]、医学图像标注[3]和故障诊断[4]等领域得到广泛应用。1992年，基于投票机制的委员会方法(Queryby-Committee，QBC)一经提出就得到了人们极大关注[5]，该算法根据成员的投票结果选择样本。之后，基于委员会的查询方法被不断改进。熵作为信息量的衡量标准走进了人们的视野。文献[6]将信息熵用于硬件木马检测。Li等[7]提出了一种基于信息熵和博弈论的混合遗传算法，该算法克服传统遗传算法容易陷入局部最优的缺点，获得更好的性能。Liu等[8]提出了新的指数熵函数作为图像纹理平滑的指标。李衡等[9]将信息熵引入桩基信号特征提取与识别算法中，得到了较好的识别效果。在主动学习方面人们利用熵来度量样本的不确定性。熵值装袋算法(entropy queryby-bagging algorithm,EQB)[10]的优势在于其结果与分类器的种类无关，可以使用任何种类的分类器。Copa等[11]指出熵值存在多值偏置问题，即选择样本时会倾向于选择同一种类的样本，这会使得分类器不能泛化，导致分类结果的不理想。针对这一问题，李宠等[12]提出了平均熵值装袋查询算法(aEQB)，该算法利用待分类数据的种类数来惩罚熵值，使其可以得到较好的分类效果。Copa等[11]提出了归一化熵值装袋查询算法(nEQB)，通过预测类别数的对数项对熵值进行归一化处理，改善了熵值的多值偏置问题。但是对于多分类问题，基于熵值的不确定度查询算法的效果可能并不理想。陈荣等[13]研究发现,样本的不确定性不能由熵值完全决定，会出现熵值小的样本比熵值大的样本的不确定度还要高的情况。

通过对上述方法的分析，本文提出二次样本筛选的高光谱图像分类算法。首先，采用超像素分割选择区域边缘的不确定性较高的样本。然后，利用信息熵在不确定度较高的样本中进行二次选择，挑选出更有价值的样本。

1 二次样本筛选的分类算法

Demir等[14]通过实验表明，在选取样本的过程中，选取样本越多，熵值装袋算法的性能越好。这表明基于熵值装袋算法只能确定样本信息量的大致分割范围，而不能按照信息量大小对样本进行准确的排列。为了使得熵值装袋算法能够更好地选取不确定度高的样本，本文提出在未标记样本集中进行一轮样本筛选，选取出未标记样本集中不确定度较高的样本，再利用主动学习策略在不确定度较高的样本中进行二次样本筛选。本算法在分类模型的训练过程中仅利用了较少的标记样本和未标记样本中不确定度较高的部分样本。相较于传统的主动学习算法使用样本少。图1为样本二次筛选算法的结构框图。

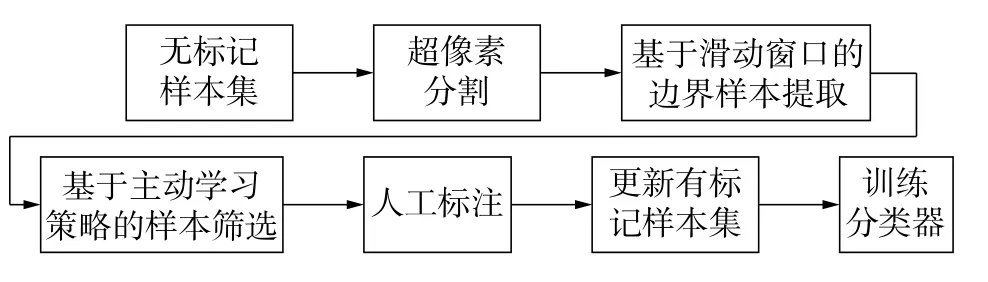
图1 样本二次筛选算法的框图

1.1 区域样本筛选

本文通过改进的SLIC算法[15]进行区域样本选取。

每个超像素内的像素视作同类地物，这样位于超像素边缘位置的像素也就是位于多类之间的像素。这样像素的特征并不鲜明，在分类时容易误判，具有较高的不确定度，利用价值很高。改进的SLIC算法在初始化网格时采用六边形网格而不是传统的正方形网格。这样做的好处是：可以更大程度地利用周围的空间信息，从而更好地减少边界像素的距离失真。同时该算法利用光谱信息和空间信息计算像素到聚类中心的距离，最大限度地利用图像信息。六角形网格如图2所示。

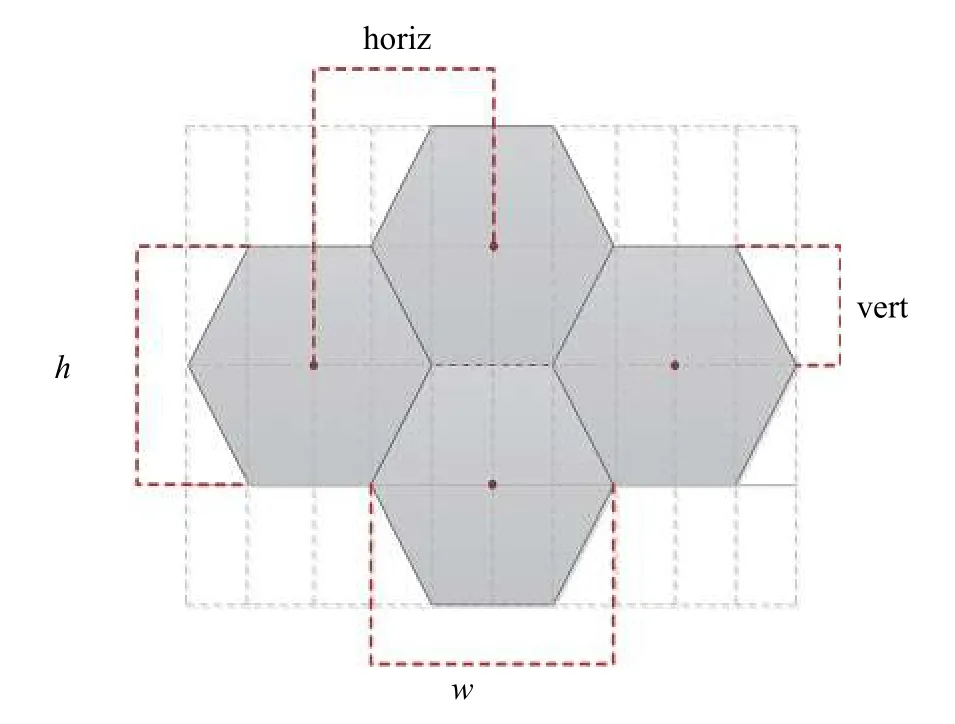
图2 初始化超像素模型

图2中，ω为六边形的宽度，h为六边形的高度，相邻六边形的水平距离用horiz表示(公式中用whoriz表示)，垂直距离为vert(公式中用hvert表示)。在搜索过程中，在2ω×2ω大小的窗中搜索与中心像素相似的像素，六边形中心的计算可以用矩阵乘法进行简单的表示

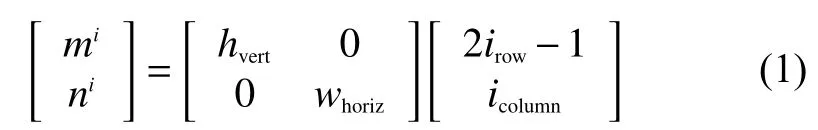
式中：超像素的中心像素的坐标为(mi,ni)；irow为超像素的行索引；icolumn为列索引。

为了充分利用图像中的空间信息，本算法将光谱距离和空间距离进行加权求和，用得到的距离作为像素到聚类中心的距离。本算法中，用欧氏距离来衡量每一像素到聚类中心的空间距离，计算公式如下

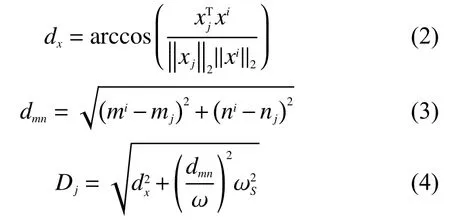
式中：光谱距离dx为光谱角距离(spectral angle distance，SAD)；空间距离dmn为欧氏距离；Dj为每一像素xj与聚类中心Ci的距离；因为空间距离dmn的变化较为明显，所以用六边形的宽度ω对其进行归一化处理；ωS为衡量空间相似度和光谱相似度之间的权重，ωS越大，空间相似度就越重要，超像素越紧密，其大小、形状也更加规范，衡量相似度时，光谱相似度比空间相似度更为重要，因此在实验中将ωS设置为0.3。参数ω用来控制超像素的平均面积进而调整其数量P，只要可以得到高光谱图像的尺寸及超像素的尺寸ω，P就可以通过将超像素的最大行索引和最大列索引相乘得到。

图3给出了改进的SLIC算法的分割结果，其中图3(a)图代表Pavia大学数据集的分割结果，图3(b)图代表肯尼迪太空中心（Kennedy Space Center，KSC）数据集的分割结果。

图3 改进的SLIC算法的分割结果

由图3可知，在平滑的中心区域超像素的形状呈现较为规则的六边形，在边界处超像素的形状规则性较差，由于ω设定为7，所以超像素的面积较小，个数较多,每个超像素的面积也更为平均，分割效果更好。

在区域划分之后，将整幅较大的高光谱图像分割为许多较小的超像素，并且为每1个超像素中的像素贴上伪标签(假设同属于1个超像素内的样本为一类，它们的伪标签相同)。本算法利用滑窗机制来实现第1轮样本筛选。在滑动窗口的过程中，若窗口内的像素分属几个类别(即类别数大于1)，则将窗口内的全部样本选择出来，在本文中这样的样本定义为边界样本。如图4所示。

图4 滑窗示意

图4中的数字表示每1个样本的伪标签，滑动窗口的大小为2×2。图中虚线框中的样本即为边界样本(图4中仅画出窗口在第1行和第2行滑动时的效果图)。在窗口滑动的过程中，若判定窗口内的样本为边界样本，则将整个窗口内的样本的伪标签全部置为0。在滑窗结束后，所有伪标签为0的样本都被视为边界样本。

1.2 信息熵二次筛选

信息是一个很抽象的东西，最初人们并不能用一个具体的指标去衡量信息的多少。直到1948年，信息熵的提出使得人们可以具象的描述信息量。之后信息熵这一概念被广泛地应用于各个领域。信息熵作为衡量样本不确定度的指标被引入主动学习，产生了熵值装袋算法。

本文通过熵值装袋算法来进行第2次的样本筛选。接下来介绍3种熵值装袋算法。

1)EQB算法

通常情况下，样本的不确定性与熵值成正比。因此EQB算法将熵作为衡量不确定度的指标。式(5)中xi表示未标记样本，H(xi)是xi的信息熵

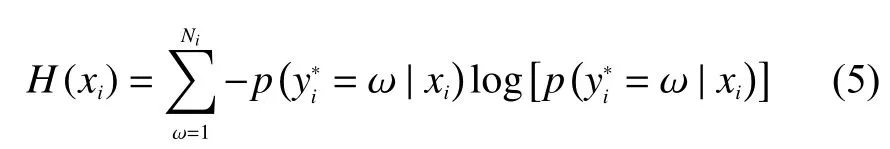
在多分类问题中，分类器将样本分为更少的类，表明样本的信息量较少。分类器将样本分为更多的类，表明样本的信息量更丰富。EQB由式(6)定义

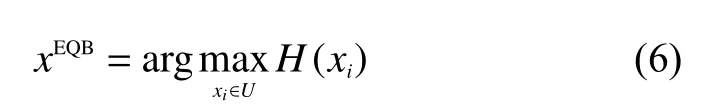
式中U为未标记样本集。

2)nEQB算法

nEQB算法可以有效地改善多值偏置问题，该方法使用1个包含预测类别数的对数项来惩罚多值问题，nEQB由式(7)定义

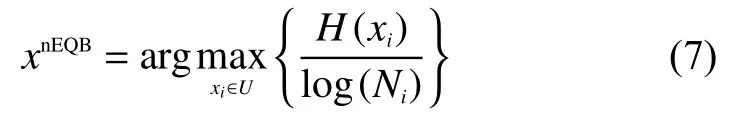
3)aEQB算法

aEQB算法通过加入1个待分类数据集中的种类的数量来惩罚多值属性，aEQB由式(8)定义

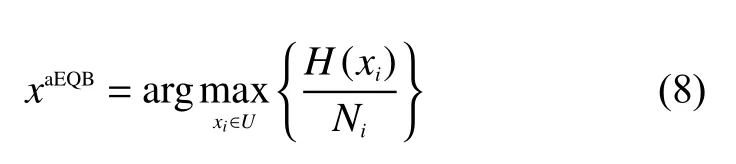
2 实验结果与分析

2.1 高光谱实验数据集

本文使用PaviaU、PaviaC和Salinas数据集进行实验。PaviaU数据集共有9种地物，全部参与实验，其中训练集占23%,共有270个标记样本；在PaviaC数据集中选择除去第1类地物和第8类地物以外的样本进行实验，其中训练集占58%，在训练集中每类选择5个样本作为有标记样本，共计35个。在Salinas数据集中选择样本数量较多的8类地物参与实验，其中训练集占57%，训练集中共有240个有标记样本。每次实验会迭代100次，共重复10次，取平均值得出实验结果。

2.2 数据分析

表1和图5是PaviaU数据集的实验结果。

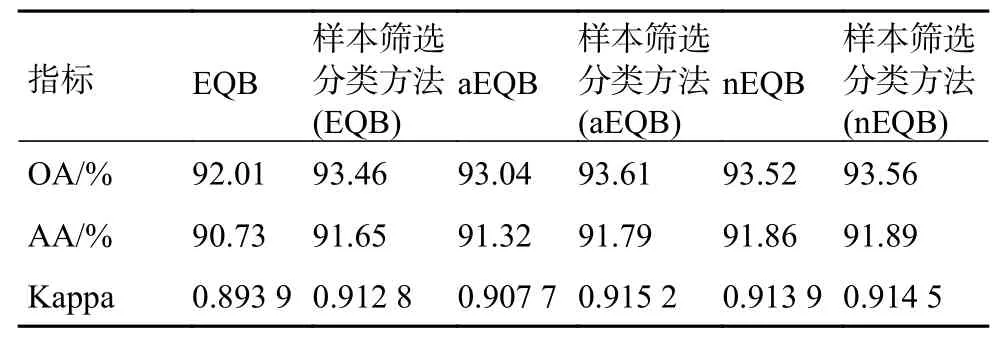
表1 PaviaU数据集实验结束时的各种精度对比

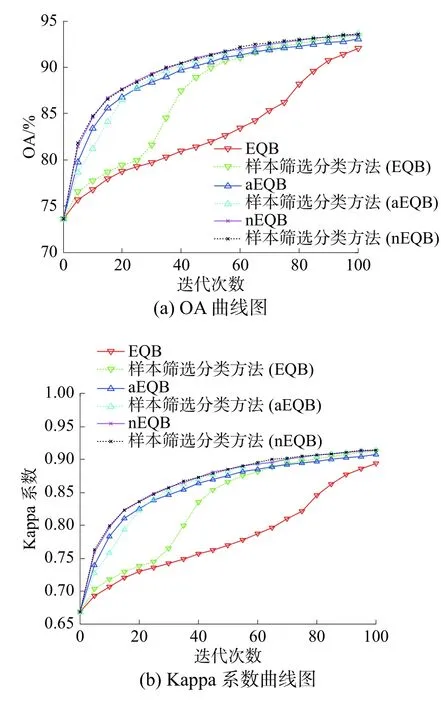
图5 PaviaU数据集的仿真结果

在OA方面，改进算法与EQB算法相比提高最多为1.45%；与nEQB算法相比提升最少为0.04%；与aEQB算法相比提升0.57%。在所有的6种算法中样本筛选分类方法(aEQB)的OA最高为93.61%。从Kappa系数来看，EQB算法的Kappa系数最低为0.893 9，样本筛选分类方法(aEQB)的Kappa系数最高为0.915 2。

表2和图6是PaviaC数据集上的仿真结果。对于OA来说，所有算法在实验结束时的OA都达到91%以上，改进算法与EQB算法相比提高1.81%；与aEQB算法相比提高0.09%；与nEQB算法相比没有提升。在AA方面，EQB算法的AA最低为91.32%，nEQB算法和改进算法的AA相同且最高为94.76%。

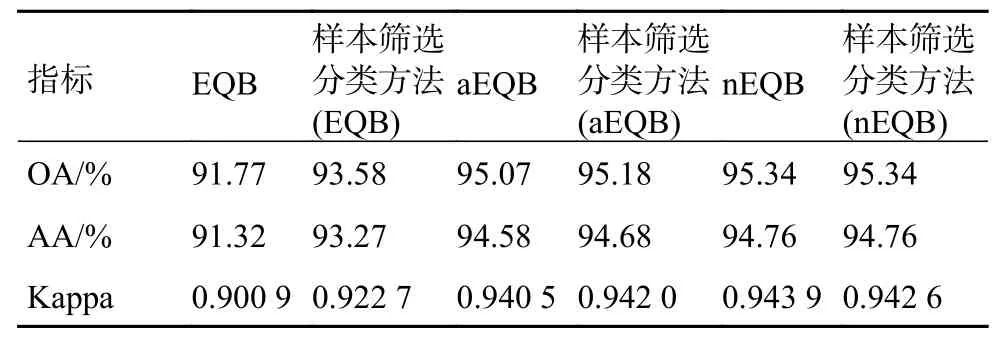
表2 PaviaC数据集实验结束时的各种精度对比

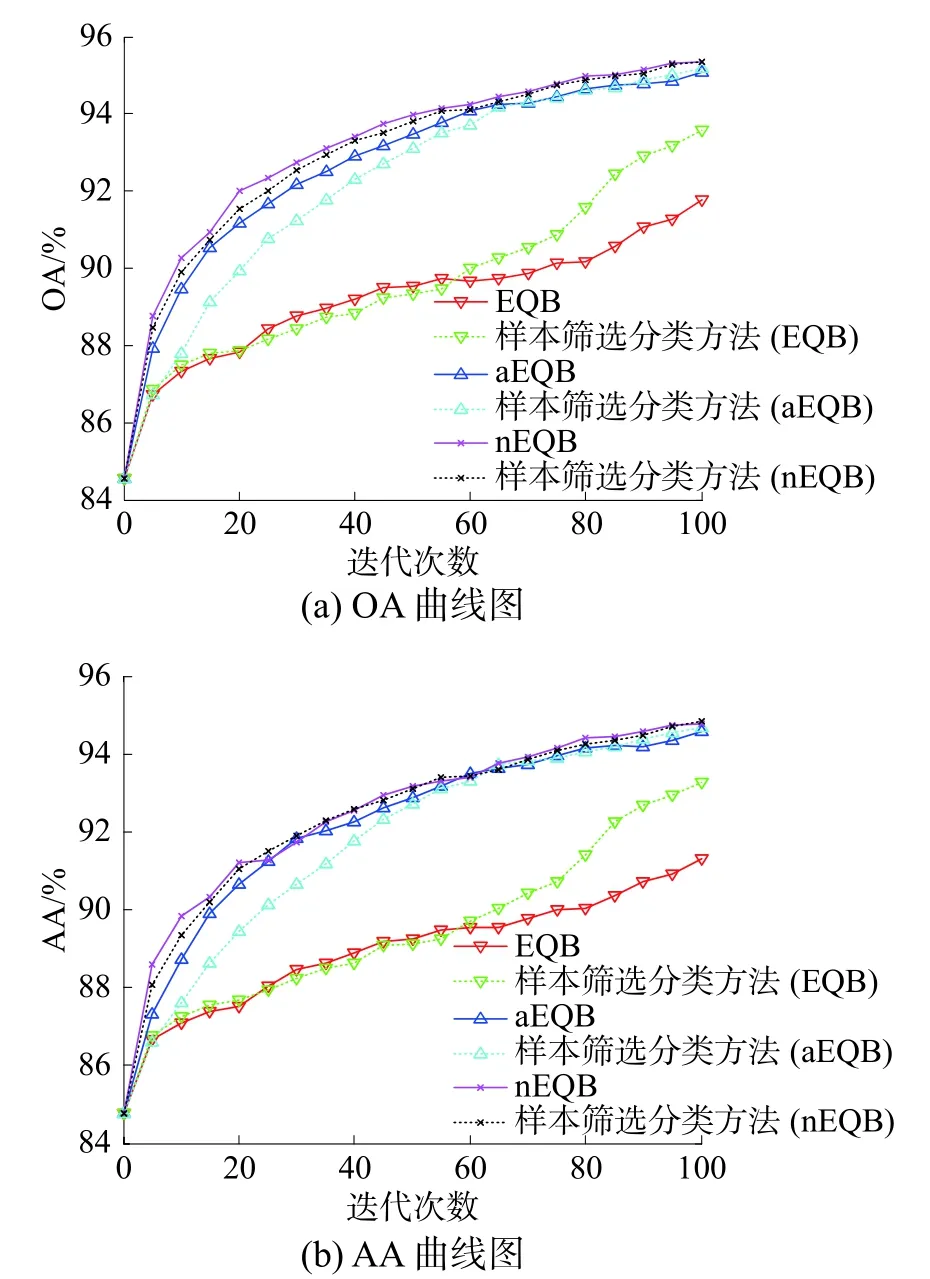
图6 PaviaC数据集的仿真结果

表3和图7是Salinas数据集上的仿真结果。在OA方面，改进算法与EQB算法相比提高最多为0.16%；与nEQB算法相比提升最少为0.02%。在所有的6种算法中样本筛选分类方法(EQB)的OA最高为91.06%。从AA来看，aEQB算法的AA最低为94.10%，样本筛选分类方法(nEQB)的Kappa系数最高为0.893 6。

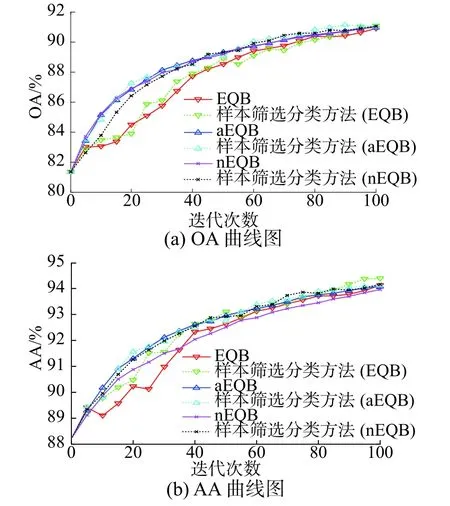
图7 Salinas数据集的仿真结果

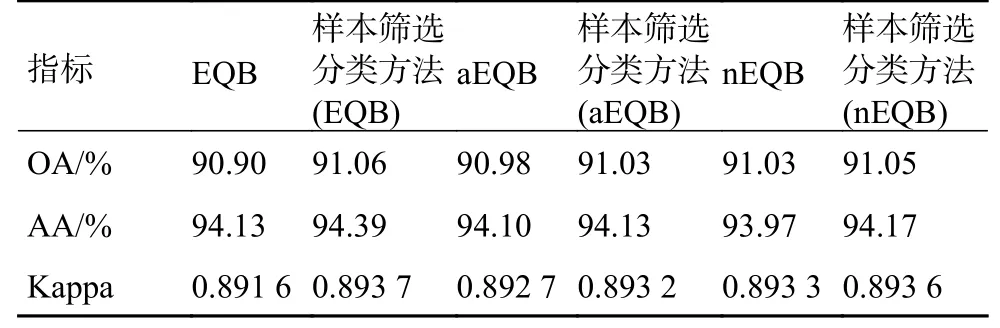
表3 Salinas数据集实验结束时的各种精度对比

3 结论

本文对于熵值装袋算法中熵值不能完全决定样本的不确定度的问题，提出样本的二次筛选策略。第1次筛选，利用SLIC算法将高光谱图像进行区域分割，提取不确定度较高的样本；第2次筛选，利用熵值装袋算法对不确定度较高的无标签样本进一步筛选，选择信息量丰富的样本进行人工标注。在训练分类器的过程中，本算法仅利用了有标签样本和未标记样本中位于区域边缘的不确定度较高的部分样本。相对于传统的主动学习策略，本算法使用的样本数量相比之下少很多。实验表明，在PaviaU数据集上改进算法相比于基础算法在各种精度上均有提高。在PaviaC数据集上改进算法相比于EQB算法、aEQB算法在各种精度上均有提高，与nEQB算法相比并无提高。在未来的工作中，在一次样本筛选时，可以采用其他的图像分割算法进行实验，对于不确定度高的样本采取不同策略结合，讨论图像分割算法和不同熵值计算对分类结果的影响。