FRACOD模拟裂纹扩展液-力耦合模块的研发及工程应用

沈宝堂，柴顺杰，张士川，陈 兵

(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛 266590；2.澳大利亚联邦科学院矿物资源部 昆士兰先进技术中心，澳大利亚 昆士兰州 布里斯班 4069)

随着地热能开发、CO2封存以及核废料封存等相关问题受到人们的日益关注，针对岩石工程领域耦合问题的研究显得尤为重要，其中岩体中液-力复杂的耦合过程作为解决岩石工程耦合问题的核心成为学者们研究的热门课题[1]。目前，研究液-力耦合问题的方法主要有室内岩石试验、现场试验以及数值模拟。室内岩石试验因可直观展示裂纹扩展与传播的优点得到了广泛的应用[2]。然而，岩石试样在取芯过程中往往受取芯设备较大的扰动影响，岩样离散性较高，导致同组试样之间试验结果存在较大偏差。现场试验可真实反映实际工程问题，但是受工程成本以及现场试验过程中复杂性及不确定性的影响，现场试验的开展受到制约[3]。数值模拟既可避免取芯设备扰动的影响，又能降低工程成本，且可应用于各种地形、地质与施工条件，故数值模拟软件被广泛应用于液-力耦合问题的研究[4]。

在过去的几十年里，学者们针对液-力耦合过程问题开展了大量数值模拟研究。研究过程中大多把岩体视为连续介质，基于有限元方法开展相关研究。然而，有限元方法需要对重点研究区域网格细化，计算工作量大大增加，严重影响着研究工作的开展[5]。针对有限元方法存在的问题，学者们展开了非连续介质的研究，主要有离散元法和非连续变形分析方法(discontinuous deformation analysis，DDA)两种。离散元法最初是由Cundall提出用来解决非连续介质问题的数值模拟方法[6]。钱庆波等[7]基于离散元法的PFC对花岗岩新生裂隙的萌生扩展过程进行了模拟，确定新生裂隙的类型及扩展过程，分析花岗岩不同类型新生裂隙的阶段性变化。DDA方法是一种基于岩体介质非连续性发展起来的数值分析方法[8]，Kim等对其作了扩展[9]，使用Louis公式和Darcy定律描述渗流，并成功进行了裂隙渗流的数值模拟。此外，沈宝堂等[10]开发了能够模拟复杂裂纹扩展的软件FRACOD，并进行了大量的工程应用[11-12]，应用结果验证了该软件模拟的准确性。

在岩石断裂耦合领域，FRACOD作为模拟单一场混合裂纹扩展的有效方法得到了推广与应用。本研究在FRACOD模拟单一场混合裂纹扩展的基础上进行模拟液-力耦合场相关功能的开发，并从理论基础方面对液-力耦合模块进行介绍。为了验证液-力耦合模块的模拟效果，选取两个应用实例对其进行模拟分析，其结果对解决实际工程问题具有指导意义和参考价值。

1 FRACOD中的液-力耦合模块

1.1 理论基础

工程中常遇到的砂岩、泥岩等岩体，水流在岩石中的流动分为裂隙内流动和向完整岩体部分渗透两部分。对于渗透性较低的花岗岩等坚硬岩石，一般认为水在岩石中为裂隙内流动，如图1所示。当岩石裂隙中的水压达到一定程度时，可引起裂隙起裂，裂隙孔径变大，甚至会导致裂隙的扩展，进而改变岩石的应力场。由于应力场发生改变，裂隙得以进一步扩展，从而使得渗透系数发生变化，形成新的流动路径。因此利用位移不连续法(displacement discontinuity method,DD)[13]开展裂隙岩体中水和力之间动态相互作用的研究是解决液-力耦合问题的关键。

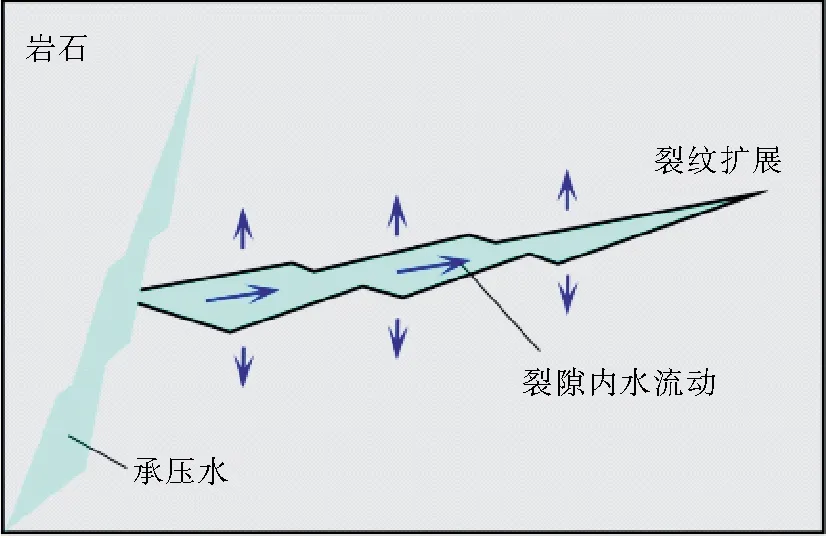
图1 裂隙流动占主导地位的流动系统

1.2 计算区域划分

裂隙内部的流动主要是“通道”流动或裂隙流动，而岩石内部则是渗流。液-力耦合的研究主要集中在岩石裂隙中的流体流动，但流体从裂隙到完整岩石的流动也被考虑在内，其具体计算区域如图2所示。

图2 划分流体流动计算的区域[14]

采用位移不连续法进行力学数值计算时，将裂隙划分为若干个位移不连续单元。在计算流体流动的过程中，将每个位移不连续单元都看作一个液压区域，相邻区域之间相互连接，在压差的影响下，流体从一个区域流向另一个区域。流体从区域i流至区域j的流量为Qij，而流体从区域i流至完整岩石的流量为Qir。

1.3 迭代求解

利用图3所示的迭代方案可以数值求解液-力耦合的问题，迭代步骤具体如下：

图3 液-力耦合的迭代过程

1)流体在裂隙区域之间的流动和裂隙区域与完整岩石之间的流动。裂隙区域间的流体流动可以用立方定律来计算，即利用方程(1)计算两个相邻区域之间的流量：

(1)

式中：e—两个区域的平均裂隙孔径；l—区域单元长度；ΔP—相邻单元之间压力差；μ—流体黏度。

由于受到完整岩石模拟裂隙厚度的影响，故假设裂隙封闭，存在恒定的流体压力作用于裂隙面边界上，且“有效”渗漏距离是确定的。流体在裂隙区域与周围完整岩石之间的流量可通过方程(2)计算：

(2)

式中：k—岩石渗透率；d—有效渗漏距离；P—区域流体压力；P0—初始孔隙压力。

2)裂隙中流体流动引起区域流体压力的变化。假设Δt时间段内流量是恒定的，这段时间结束后，由于流体的流入及流出，会使得区域内流体的体积发生变化，进一步导致区域内流体压力有所改变。区域内流体压力可通过方程(3)计算：

(3)

式中：Kw—流体体积模量；V—区域体积；Δt—时间步长。

3)流体压力的改变导致裂隙的变形。裂隙表面流体压力的增大或减小会导致裂隙的张开和闭合，采用DD法计算裂隙变形时，将裂隙区域中新的流体压力作为输入边界压力。考虑裂隙区域(单元)流体压力后，由方程(4)给出用于计算单元位移不连续变化的方程组：

(4)

式中：(σs)0，(σn)0—裂隙单元的切向应力及法向应力；Ds，Dn—裂隙单元切向和法向上的不连续位移；Ass，Asn，Ans，Ann—裂隙单元影响系数；Ks，Kn—裂隙切向和法向刚度。

4)裂隙变形导致区域单元体积的变化，从而改变了区域内流体压力，利用方程(5)计算新的区域压力：

(5)

式中：P′(t+Δt)—裂隙变形前的初始区域压力；P(t+Δt)—裂隙变形后新的区域压力；Δe—裂隙孔径变化量。

步骤4)结束以后，在步骤1)中使用新的区域流体压力来计算区域间的流量，重复步骤1)至4)，直到裂隙变形达到稳定状态。

2 基于FRACOD液-力耦合模块的案例分析

FRACOD在矿柱剥落、水力压裂[15-16]等方面获得了广泛应用，并取得较好的结果，但这些均属于单一应力场方面研究。为此在FRACOD已有研究基础上开发了液-力耦合新功能，可实现多个领域液-力耦合工程问题的模拟。为了验证该模拟软件液-力耦合模块的模拟效果，以地热开发中水力压裂模拟和节理岩体中裂纹传播过程的模拟为例，进行液-力耦合环境下裂纹扩展问题的分析。

2.1 地热开发中水力压裂模拟

干热岩地热开发具有高清洁性、储量丰富性、运行稳定性和空间分布的广泛性等优点，成为世界各国研究和开发的重点。而在干热岩开发的过程中，通过水力压裂的方法激发储层并联通注入井和生产井是开发的关键所在[17-18]。但由于现代探测手段的局限性，往往很难准确检测到裂隙发育的动态演化过程，特别是在液-力耦合场的影响下，因此数值模拟研究方法的重要作用日益凸显。

水力压裂模拟选取三条相交裂隙连接的岩体内注入井和生产井为研究对象。假设井孔直径为1 m，两井间距为20 m，其中注入井施加的流体压力恒定为6 MPa；另一个生产井施加的流体压力恒定为0。

模拟中涉及的主要参数为：流体体积模量K=2 GPa，流体黏度μ=1×10-3Pa·s，完整岩石渗透率k=1×10-19m/s，地应力σxx=5 MPa；σyy=10 MPa，断裂起始孔径e0=10 μm，岩石杨氏模量E=60 GPa，泊松比ν=0.25，断裂剪切和法向刚度Ks=Kn=100 GPa/m，断裂摩擦角φ= 30°，断裂黏聚力c=0，裂缝张开角φd=1°。主要对液-力耦合场下裂隙滑移和扩张的耦合过程进行模拟。模拟达到稳态时的最终结果如图4所示，其中箭头的方向分别表示水压、剪切位移、流速及水力孔径扩展的方向，箭头的大小则表示水压、剪切位移、流速及水力孔径扩展的大小。

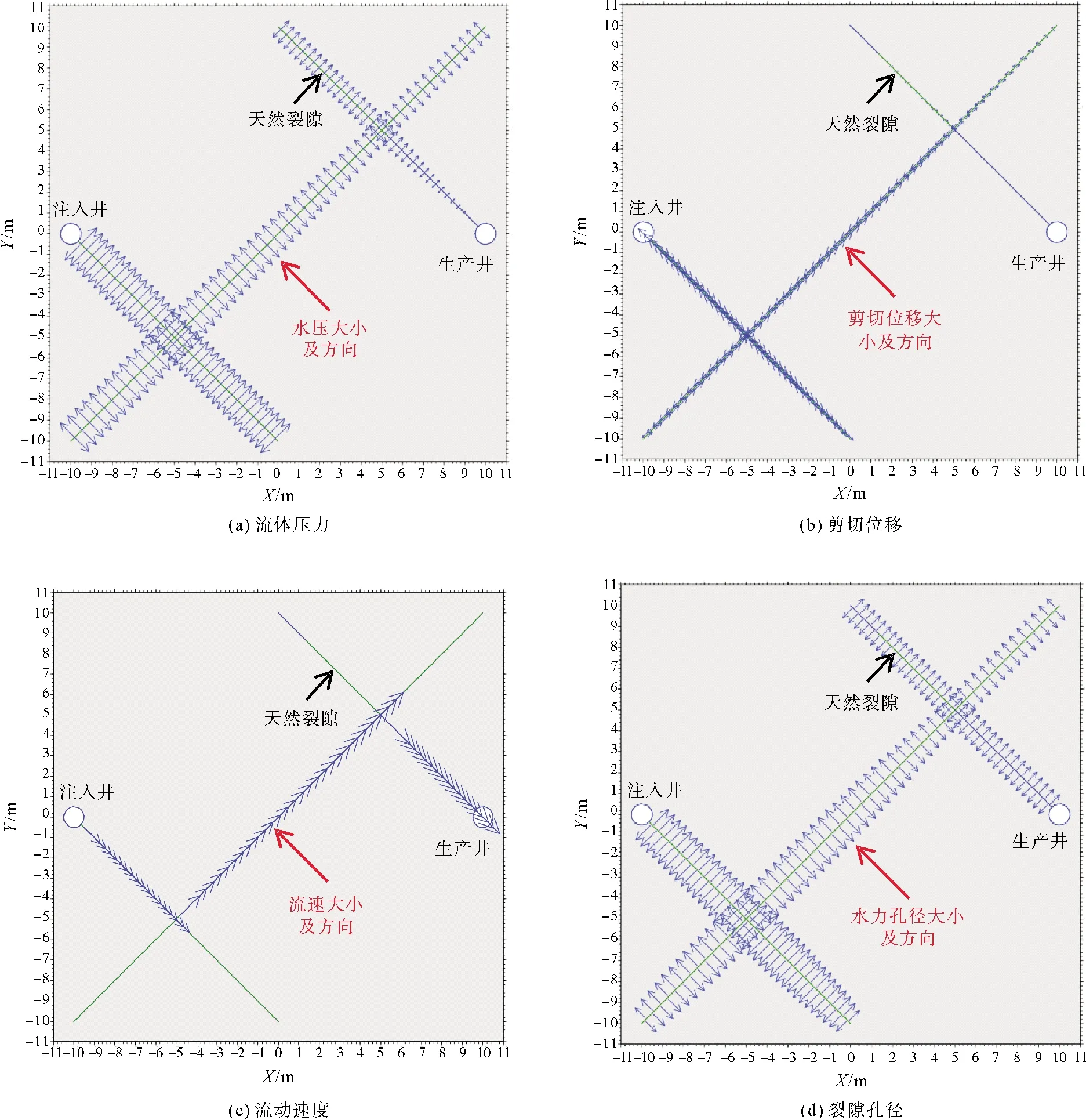
图4 裂隙流体流动、裂隙剪切和裂隙扩展耦合过程的稳态解

达到稳态后的流体压力分布如图4(a)所示，由图可以看出，在恒定流体压力的作用下，注入井附近水压较高，沿着天然裂隙向生产井方向流动的过程中水压逐渐降低，直至为0，流动过程中水压方向始终垂直于裂隙面；剪切位移的分布如图4(b)所示，在水压的作用下，天然裂隙发生剪切破坏，从而造成裂隙的大规模滑移，由图可知，在不同水压的影响下，与注入井相连通的裂隙剪切位移较大，而与生产井相连的裂隙剪切位移较小甚至没有产生剪切位移；流动速度的分布则如图4(c)所示，流体从注入井沿裂隙流向生产井的过程中，由于天然裂隙的大规模滑移和剪切，导致裂隙孔径增加，使得流速明显增强，同时，流体沿最短裂隙路径进行流动，封闭的裂隙端头未发生流体流动；图4(d)的模拟结果显示了裂隙水力孔径扩展的情况，与剪切位移分布图对比可以看出，水力孔径大小与剪切位移大小的变化规律相似，受裂纹剪切的影响，裂隙中的水力孔径增加了80%。

该案例表明液-力耦合场对岩体中天然存在的裂隙的稳定性和运动具有显著影响，水力压裂会造成天然裂隙的大规模滑移和剪切，进而引起裂隙孔径的变化和流体流动的增强。该模拟结果与前人研究[19]结论相吻合，验证了液-力耦合模块的可行性与准确性，进而可对增强型地热系统中干热岩的水力压裂方案设计和提高注采效率等有直接的工程指导意义。

2.2 节理岩体中裂纹传播过程的模拟

在高水压和地应力相互作用环境下，难以通过试验手段获取含水裂纹传播过程中的水压流量特征、岩石应力场和声发射事件的变化规律[20]。实际地质环境中岩石节理广泛存在，因此探究液-力耦合作用下裂纹在节理岩体中的起裂规律成为裂纹传播过程的关键。本模型采用中心点对称形式，在中心点处设置一个直径0.1 m、水压6 MPa的进水孔，模拟地应力环境Sxx=Syy=1 MPa，如图5所示。进水孔设置较小尺寸的预制裂纹，裂纹初始宽度为10 μm，裂纹在液-力耦合作用下发生起裂；节理裂隙群平均分布于裂纹传播扩展范围内，且节理之间互不贯通，节理与水平方向夹角为45°。模型中涉及主要参数：抗拉强度Rm=2 MPa，弹性模量E=37.5 GPa，岩石孔隙率n=0.1，内聚力c=33 MPa，内摩擦角φ=33°，岩石泊松比ν=0.25，流体体积模量K=2.0 GPa。

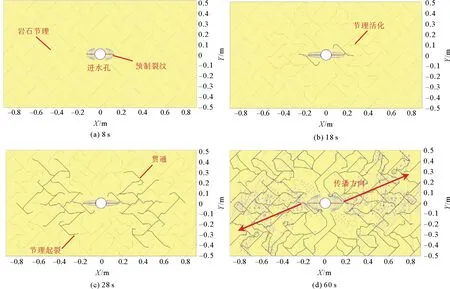
图5 液-力耦合作用下裂纹的起裂、扩展和贯通

1)裂纹起裂、扩展和贯通

图5为模拟8、18、28和60 s过程中液-力耦合作用下裂纹的起裂、扩展和贯通过程。模型计算8 s后，由于水压大于地应力，预制裂纹在水压的作用下沿着裂纹方向往两端扩展(图5(a))，裂隙水压沿着扩展方向逐渐降低。18 s后，裂纹与岩石节理贯通，高压水进入岩石节理(图5(b))，在水压的作用下，岩石节理两端沿水平方向发生扩展，同时，引起周围部分节理活化。28 s后裂纹贯通大多数节理，呈扇形分布(图5(c))，岩石节理向扩展范围内最大主应力方向传播。60 s后裂纹已贯穿全部的节理(图5(d))，裂隙水主要通过节理群向水平方向流动，说明节理裂隙群内水的流动方向受地应力的影响。

2)应力场分布特征

地应力和水压相互作用影响裂纹的扩展，进而影响岩石应力场的分布，图6为裂纹扩展过程中8、18、28和60 s的应力场分布图。模型计算8 s后(图6(a))，在裂纹扩展的作用下，于裂纹扩展两端产生最大拉应力，沿裂纹传播方向分布并促进裂纹传播。模型计算18 s后(图6(b))，受钻孔影响，岩石节理两端出现局部裂纹扩展现象，最大拉应力产生于钻孔附近，同时贯通后的岩石节理发生进一步扩展，与裂纹扩展应力集中区域相连接。模型计算28～60 s(图6(c)、6(d))时，裂纹扩展释放围岩集中应力，应力发生了重新分布；围岩发生破坏的区域沿最大主应力方向扩展(如箭头所示)，破碎岩体为水的流动提供传播空间。

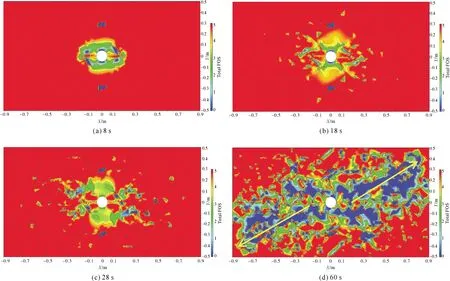
图6 裂纹扩展过程中的应力场分布

3)声发射事件分布特征

图7为裂纹扩展过程中8和28 s声发射事件分布图，其中红色为本循环声发射事件，黑色为本循环之前的声发射事件。计算8 s，受钻孔水压影响仅有钻孔附近区域的节理出现声发射事件，分布范围为5倍钻孔半径；随着裂隙水的传播(计算28 s)，节理发生错动且彼此间相互贯通，造成声发射事件广泛分布于含水节理周边，说明裂隙水的传播促进节理群的贯通，加速岩体破坏。

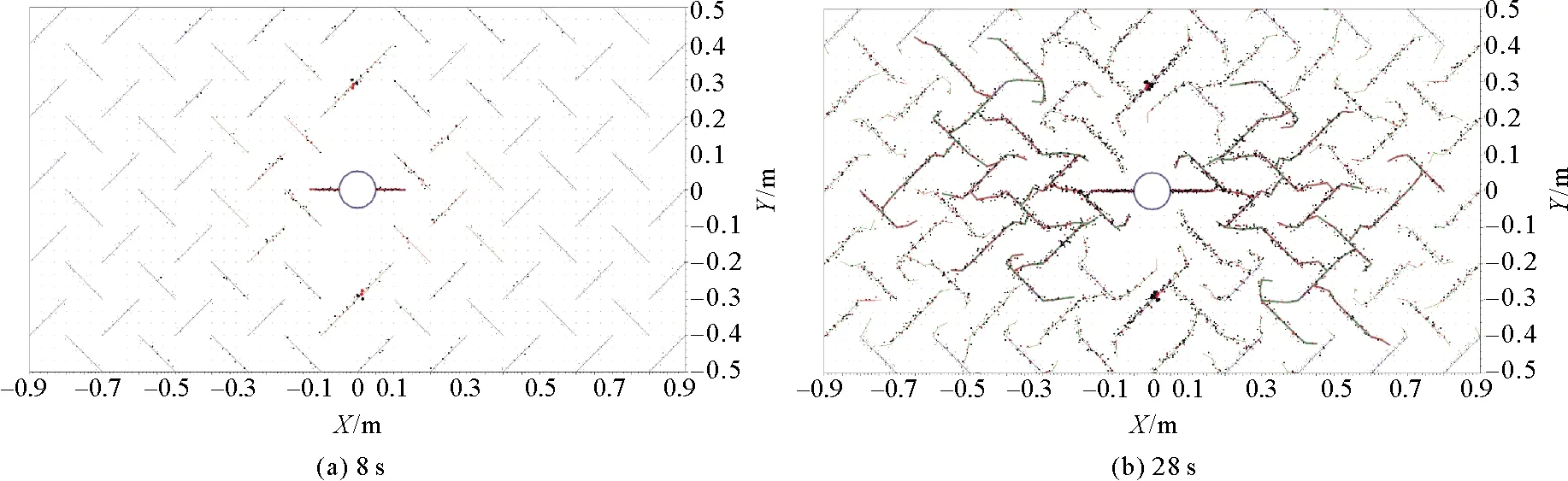
图7 裂纹扩展过程中的声发射事件分布

该案例模拟了液-力耦合作用下节理岩体中裂纹的传播过程，直观地展现了耦合裂纹的起裂、扩展和贯通全过程以及应力场、声发射等物理场信息的分布规律，在岩体破裂机理研究及工程安全评价等方面有一定的参考价值[21]。由模拟结果可以看出，在液-力耦合作用下，耦合裂纹与岩石节理贯通且节理裂纹继续向扩展范围内最大主应力方向传播。通过与前人研究[22]结果相对照，结论吻合，验证了模拟结果的准确性与合理性。

3 结论

1)开发了液-力耦合模块，采用位移不连续法对岩体力学行为进行计算及模拟，进一步基于迭代法实现了裂隙中流体流动的模拟，可以准确模拟液-力耦合环境中岩体内裂纹扩展过程及演化规律。

2)地热开发中水力压裂模拟分析结果表明，天然裂隙岩体在水压及原岩应力的共同作用下发生剪切滑移，受剪切裂纹的影响水力孔径增加了80%，流体流动明显增强；对节理岩体中裂纹传播过程的模拟分析结果显示，在液-力耦合作用下，液体驱动的裂纹与岩石节理贯通且贯通后的节理继续向最大主应力方向扩展，模型结果直观地展现了耦合裂纹的起裂、扩展和贯通全过程以及应力场、声发射等物理场信息的分布规律。两个案例模拟结果验证了液-力耦合模块模拟过程的可行性及计算结果的准确性，为研究岩石耦合断裂问题提供了一种有效手段。

本研究开发的FRACOD软件已可模拟液-力耦合场的裂纹扩展，今后还将继续研发H-T(液-热)耦合模块、H-T-M(液-热-力)耦合模块用于模拟多场耦合作用下的裂纹扩展规律及岩体破坏特征。