充填节理岩体中应力波传播特性研究

贾帅龙, 王志亮, 熊 峰, 田诺成, 卢志堂

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学 资源与环境工程学院,安徽 合肥 230009)

自然岩体中往往存在许多不连续软弱结构面,如充填节理、软弱夹层及断层等。在这些软弱结构面中一般含有如碎屑、黏土等充填材料,其不仅影响岩体的力学特性,也对应力波在岩体中的传播特性产生影响。当爆炸或地震作用产生的应力波传播到岩体不连续结构面处时,结构面处的材料与岩石接触界面均会产生变形,导致应力波发生透射和反射现象,对岩体工程的安全造成影响。因此,有必要对应力波在节理岩体中的传播机理展开研究。

关于应力波在节理岩体中传播规律的研究,国内外研究者开展了大量工作。文献[1-2]采用薄层界面模型探讨了应力波垂直与斜入射充填节理的传播特性,并与现有的理论方法进行了对比分析;文献[3]研究了应力波在单条和多条平行充填节理中的传播规律,发现透射系数随着节理条数的增加而减小;文献[4]以节理接触面积比为关键参数建立了一维接触界面模型,指出当节理接触面积比大于0.5时,一维接触界面模型可以准确呈现透射波与反射波;文献[5-6]采用改进的主频率法对应力波在岩体中的传播规律进行了分析,并提出了非线性黏弹性等效介质模型;文献[7]结合特征线法与库伦滑动模型建立了粒子与剪切应力的递推方程,得出剪切应力比是影响应力波传播特性的重要因素;文献[8]通过PFC2D软件模拟了应力波在充填节理中的传播,得出透射系数与应力波幅值和频率有关;文献[9]推导了纵波在2个节理间传播的时域方程,发现节理刚度与入射波频率对透射和反射系数有一定的影响;文献[10]考虑了地应力对柱面应力波在完整岩石中物理和几何衰减的影响,推导出柱面波在节理岩体中的传播方程,并与试验结果进行对比分析。

综上所述,对于含充填材料的软弱结构面,一般将充填节理直接简化为不考虑厚度的节理模型,忽视了充填节理性质对应力波在岩体中传播的影响。此外,岩体中岩石与充填材料之间往往存在孔隙[11],两者并不是紧密接触,在应力波的作用下节理接触界面与充填材料均会产生变形。而以往研究均假定节理接触界面为紧密接触面[1-2],不考虑节理接触界面变形的影响。因此,本文引入线弹性模型对岩石与充填材料之间的接触界面进行描述,并基于时域递归分析方法推导出应力波入射充填节理的波动方程,分析了节理接触界面刚度、节理厚度及入射角度对节理岩体中应力波传播特性的影响,并进一步通过应力均匀性假定,反推得出了充填节理的法向与切向力学特性的变化规律,该力学特性同时考虑了节理接触界面与充填材料的共同变形。研究成果可为应力波在节理岩体中传播规律的研究提供一定的理论指导。

1 理论基础

1.1 充填节理模型

充填节理主要由接触界面1、充填材料及接触界面2构成,如图1所示。分析过程中岩石和充填材料均为各向同性的均质弹性体。岩石与充填材料的接触界面采用线弹性模型,如图2所示。图2中,kn、ks分别为节理接触界面法向和切向刚度。

图1 充填节理模型

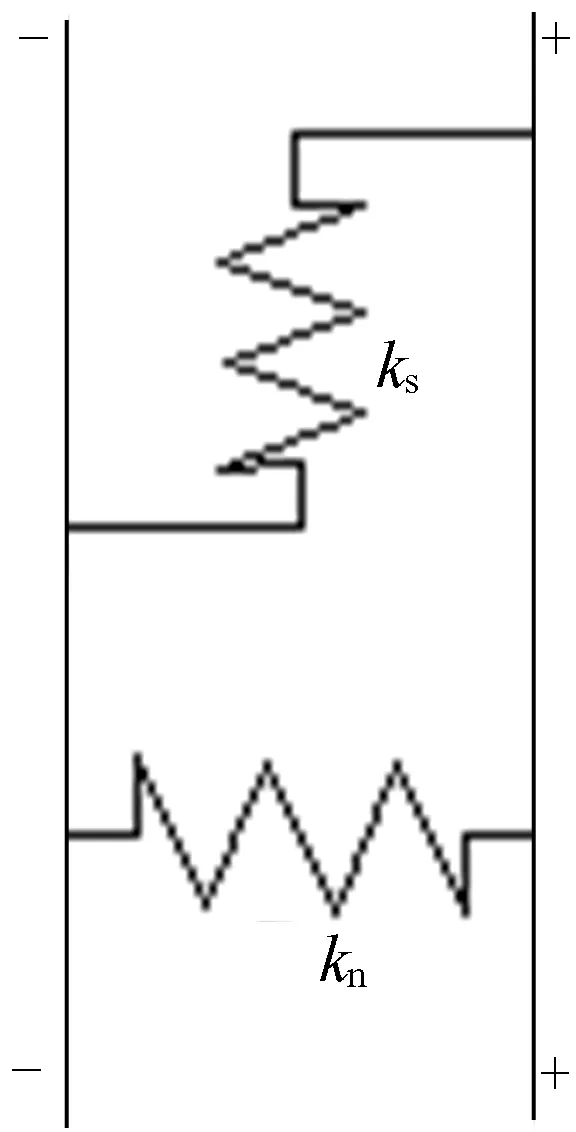
图2 线弹性模型

当应力波传播到充填节理两侧接触界面时,应力波发生透射和反射的现象,从而形成透射波与反射波。同时,应力波在充填节理界面处的传播满足Snell定理,即

(1)

其中:crp、crs(cfp、cfs)分别为岩石(充填材料)中P波和S波的传播速度;αr、βr(αf、βf)分别为岩石(充填材料)中P波与S波的入射角。

1.2 应力波在充填节理处的传播方程

应力波传播到节理接触界面处将产生透射波和反射波,因此,在岩石和充填材料中均存在4种传播方向的应力波,如图3所示,分别为右行和左行P波以及右行和左行S波。文献[12]给出了接触界面两侧法向应力σm和切向应力τm的表达式,分别为:

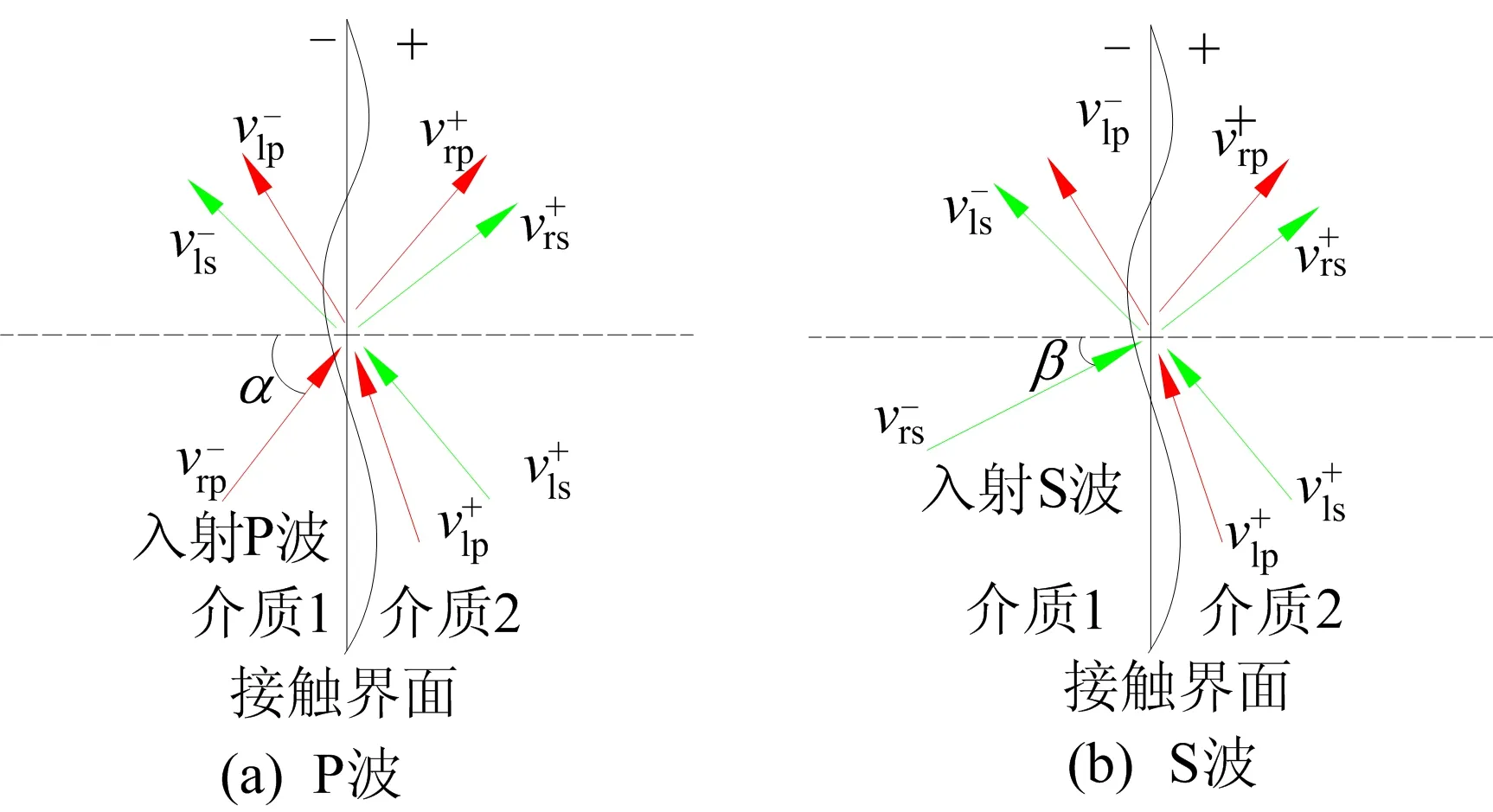
图3 节理接触界面处应力波示意图

σm=(Zpvrpcos 2β)m+(Zsvrssin 2β)m+

(Zpvlpcos 2β)m-(Zsvlssin 2β)m

(2)

τm=(Zpvrpsin 2βtanβ/tanα)m-(Zsvrscos 2β)m-

(Zpvlpsin 2βtanβ/tanα)m-(Zsvlscos 2β)m

(3)

其中:上标m表示“-”和“+”符号,分别表示节理接触界面的左侧和右侧;vrp、vlp分别为右行和左行的P波波速;vrs、vls分别为右行和左行的S波波速;Zp、Zs分别为P波与S波的波阻抗;α、β分别为P波和S波的入射角。

(vlpcosα)m+(vlssinβ)m

(4)

(vlpsinα)m+(vlscosβ)m

(5)

根据前面节理接触界面的假设,节理接触界面处满足位移不连续条件,可以得出:

σ-=σ+,τ-=τ+

(6)

(7)

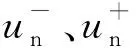
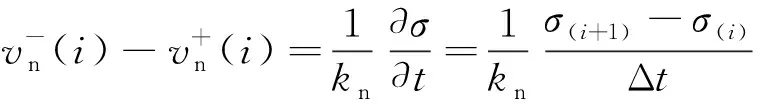
(8)

(9)

其中:i为时间参数。

将(2)式、(3)式代入(6)式,可得:

(10)

其中,下标Ⅰ和Ⅱ分别代表图1中的岩石和充填材料介质。

An、Bn(n=Ⅰ,Ⅱ)分别为:

将(4)式、(5)式代入(8)式和(9)式,可得:

(11)

其中,E、F、G、H、J、K分别为:

由以上可知,通过(10)式、(11)式可得到应力波通过接触界面1的质点振动速度。由于充填材料为各向同性的均质材料,应力波在充填节理中任意一点均满足应力与位移连续条件,因此,当应力波传播到节理接触界面2时,有

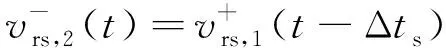
(12)

(13)

其中:下标1、2分别代表节理接触界面1与接触界面2;Δtp、Δts分别为P波与S波在充填节理中的传播时间。Δtp、Δts计算公式分别为:

Δtp=L/(cfpcosαf), Δts=L/(cfscosβf)

(14)

其中,L为充填节理厚度。

综上可知,通过(10)～(14)式即可分析出应力波在充填节理处的传播规律。充填节理中应力波的传播主要分为3个阶段:首先应力波通过节理接触界面1,其得到的左行P波和S波即为反射P波与S波;然后应力波在充填材料中进行传播;最后应力波经过节理接触界面2得到透射P波与S波。本文采用Matlab软件对理论方程进行计算,当计算节理厚度与波长比小于1/100时,计算结果的误差可忽略[13]。因此,为了均衡软件计算效率与计算结果的正确性,将时间步长Δt统一取值为1/(2 000f),f为应力波频率。

2 理论验证

为了验证所推导理论方程的正确性以及与已有理论[2]的差异,分别从应力波法向和斜入射充填节理方面与文献[2]结果进行对比。定义无量纲刚度系数Kn=kn/(Zpω),Ks=ks/(Zsω),ω为圆频率,Kn、Ks的取值范围为0.5～10.0。

分析过程中入射角度均在临界角范围内,入射P波的临界角度αc=90°,S波的临界角度βc=arcsin (cs/cp)=30.4°。岩石和充填材料的参数取值和文献[1]一致,见表1所列。

表1 岩石与充填材料参数

2.1 应力波法向入射充填节理

为了验证所推导波动方程的正确性,与文献[2]提出的薄层模型计算结果进行对比。文献[2]中岩石与充填节理的接触界面为位移连续面,而本文为位移不连续面。为降低节理接触界面变形的影响,计算过程中将节理接触界面法向与切向刚度的取值均设为100 GPa/m,进而忽略节理接触界面变形的影响。为更加清晰地研究应力波在充填节理处的传播规律,定义透射系数TKC和反射系数RKC分别为:

(15)

其中:K=P,S;vIK、vRK、vTK分别为质点入射、反射及透射波的振动速度。

分析中入射P波与S波均为1/2周期的简谐波,振幅为1 m/s,频率为100 Hz。应力波法向入射充填节理下本文与文献[2]透射与反射系数结果对比如图4所示。从图4可以看出:当P波和S波法向入射充填节理时,透射系数均随着节理厚度的增加而降低,反射系数逐渐增大;在不同节理厚度下本文与文献[2]结果有一定的差异,这是因为文献[2]中节理接触界面为不连续面,而本文中将节理接触界面刚度设定为一个较大值,节理接触界面会产生较小的变形,对应力波的传播规律造成影响。

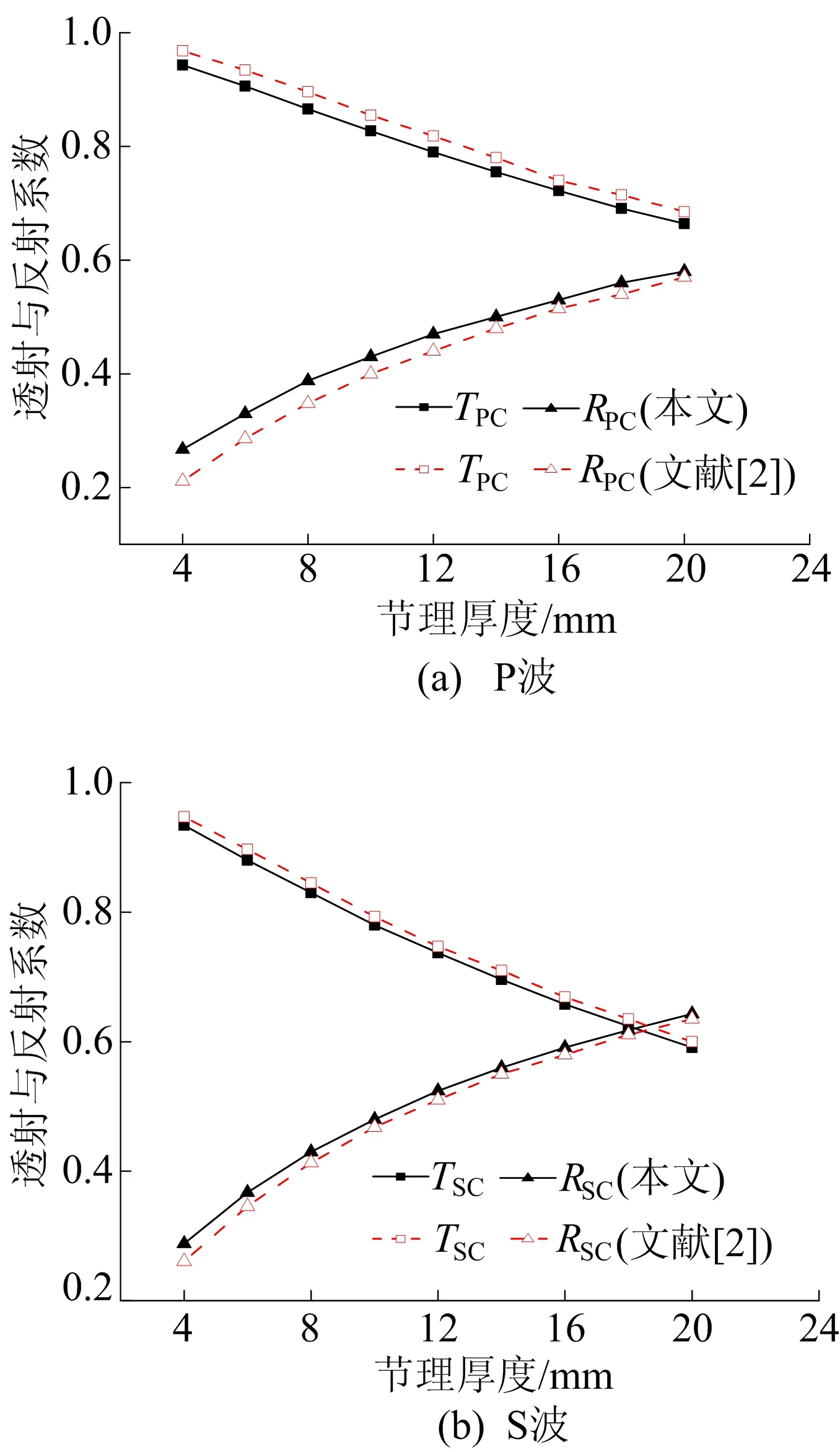
图4 应力波法向入射充填节理下透射与反射系数结果对比

2.2 应力波斜入射充填节理

应力波斜入射充填节理时,P波与S波的入射角度均设为20°。应力波斜入射充填节理下本文与文献[2]透射和反射系数结果对比如图5所示。从图5可以看出,当P波与S波斜入射充填节理时,入射波形均发生转变,形成了透射P波与S波以及反射P波与S波。通过将本文与文献[2]结果对比发现,在P波与S波入射下透射与反射系数均出现较小的差异。

图5 应力波斜入射充填节理下透射与反射系数结果对比

因此,当应力波法向或斜入射充填节理时,本文与文献[2]得出的透射与反射系数结果均呈现较小的差别,表明节理接触界面对应力波的传播特性具有一定的影响,同时,也验证了本文所推导理论方程的正确性。

3 参数分析

3.1 节理接触界面刚度的影响

为了研究节理接触界面刚度对应力波传播特性的影响,分析过程中无量纲刚度系数Kn=Ks=K,K的取值范围为0.5～10.0,充填节理厚度为8 mm,P波与S波的入射角度均为20°。应力波斜入射充填节理下透射与反射系数变化曲线如图6所示。

从图6可以看出:随着节理接触界面刚度的增加,由P波得出的透射系数TPC与S波得出的透射系数TSC均逐渐增大,但其增加幅度逐渐降低并趋于稳定;由P波得出的透射系数TSC和S波得出的透射系数TPC基本处于较小值,变化较不明显;由P波得出的反射系数RPC与RSC均随着节理接触面刚度的增加而降低,同时,其降低幅度逐渐减小。

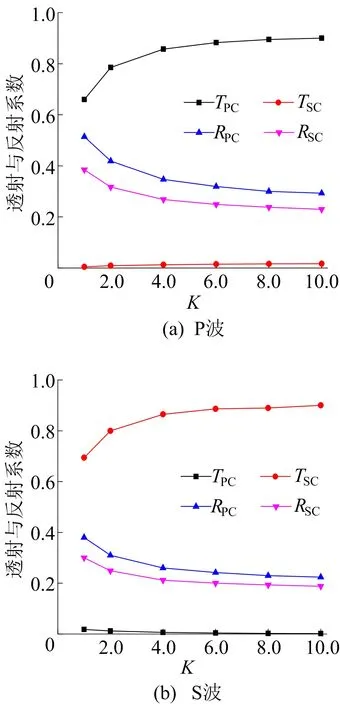
图6 应力波斜入射充填节理下透射与反射系数变化曲线

3.2 充填节理厚度的影响

以往对应力波在充填节理处传播规律的研究,一般将充填节理简化为位移不连续模型,忽视了充填节理厚度的影响。因此,有必要分析充填节理厚度对应力波传播特性的影响。实际工程中岩体中充填宽度与波长相比较小,计算过程中将充填节理厚度范围设为4～20 mm,无量纲刚度系数Kn=Ks=K=6.0,P波与S波的入射角度均为20°。不同节理厚度下P波的透射与反射系数变化曲线如图7所示。

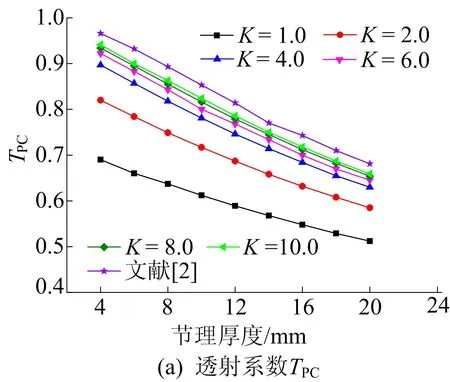
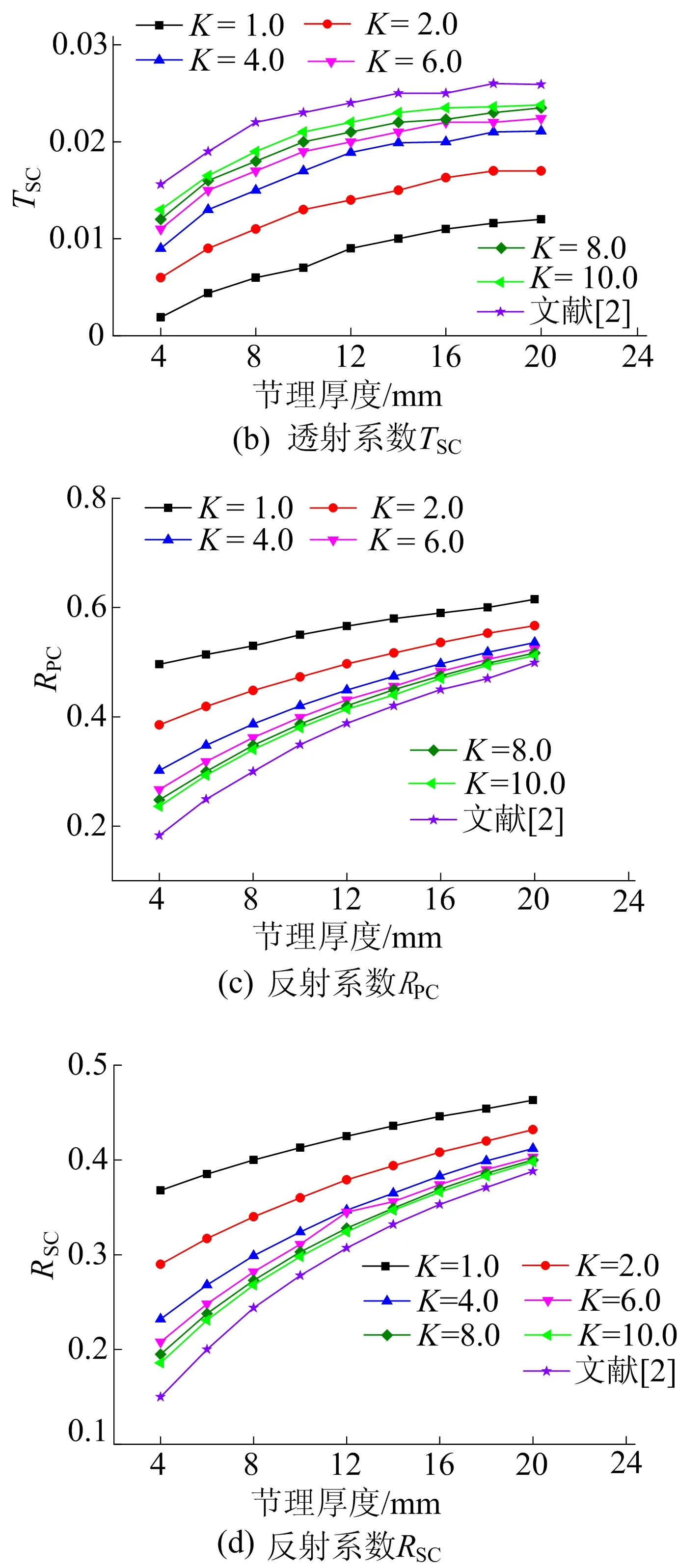
图7 不同充填节理厚度下P波的透射与反射系数变化曲线

由图7可知:

(1) 当节理接触界面刚度相同时,透射系数TPC随着节理厚度的增加而降低,反射系数RPC与RSC逐渐增大,而透射系数TSC变化较不明显。这是因为充填节理厚度越大,充填节理的等效法向与切向刚度越小,导致大部分应力波发生反射,从而透过充填节理的应力波较少。

(2) 在相同节理厚度下透射系数TPC随着节理接触界面刚度的增加而增大,反射系数RPC与RSC逐渐降低。

(3) 从文献[2]得出的结果可知,当不考虑节理接触界面变形时,透射系数TPC最大,而反射系数RPC与RSC最小。

不同节理厚度下S波的透射与反射系数变化曲线如图8所示。

从图8可以看出:在相同节理接触界面刚度下,透射系数TSC随着节理厚度的增加而减小,而反射系数RPC与RSC逐渐增大;当节理厚度相同时,透射系数TSC随着节理接触界面刚度的增加而增大,而反射系数RPC与RSC逐渐减小。

3.3 应力波入射角度的影响

为了揭示入射角度对应力波在充填节理处传播特性的影响,分析中无量纲刚度系数Kn=Ks=K=6.0,充填节理厚度为8 mm。P波在不同入射角度下透射与反射系数的变化曲线如图9所示。

由图9可知:透射系数TPC随着入射角度的增加基本保持不变,而透射系数TSC逐渐增大,当接近入射临界角90°时,透射系数TPC与TSC显著降低;当入射角度小于60°时,反射系数RPC随着入射角度的增加而降低,而入射角度接近临界角时,透射系数RPC迅速增大;反射系数RSC以45°为界限,随着入射角度的增加呈先增大后降低的规律;P波在相同入射角度下,透射系数TPC随着节理接触界面刚度的增大而增大,而反射系数RPC与RSC逐渐降低。

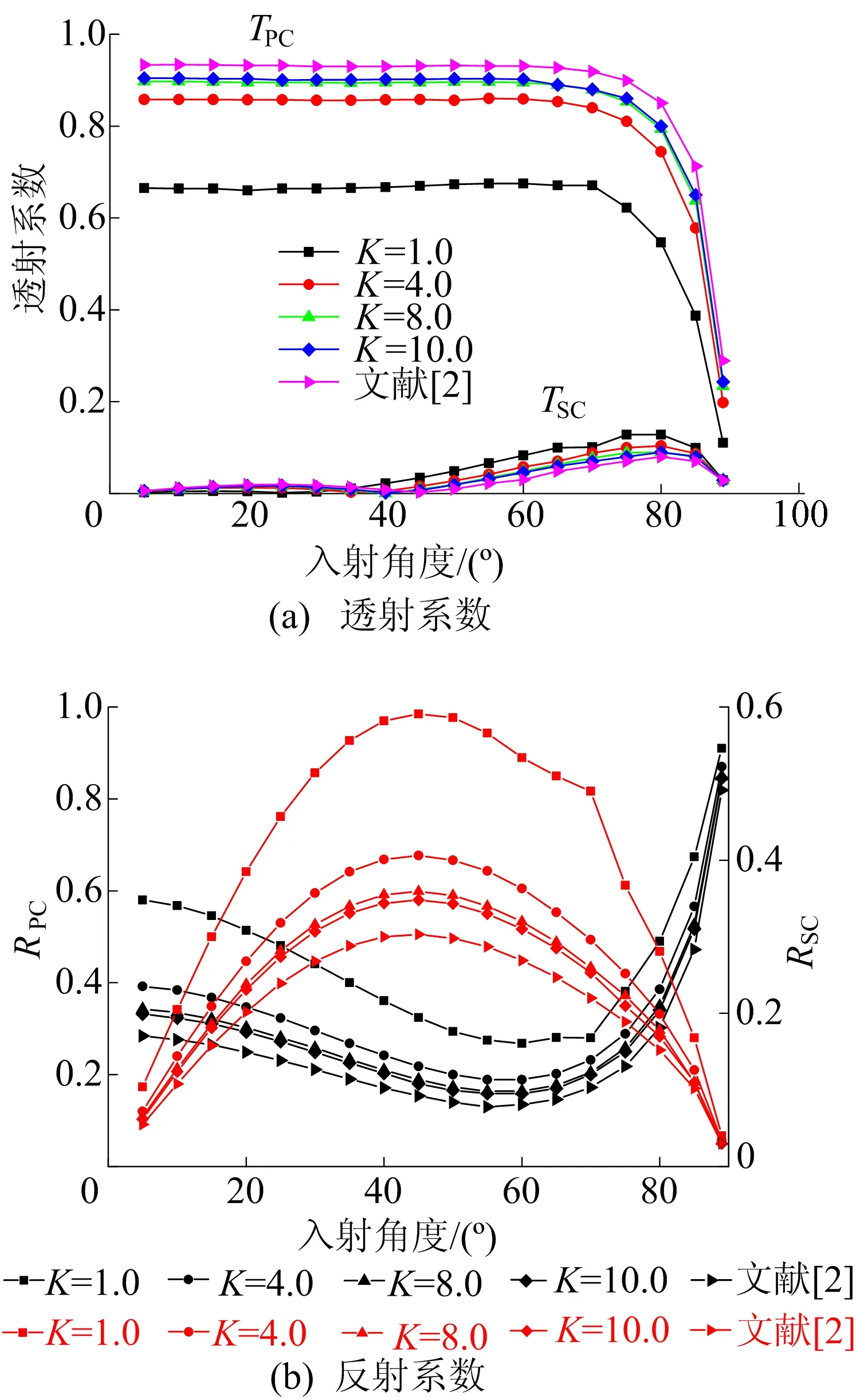
图9 P波在不同入射角度下透射与反射系数变化曲线

S波在不同入射角度下透射与反射系数的变化曲线如图10所示。由图10可知:当S波在入射临界角范围内时,透射系数TPC与TSC均随着入射角度的增加而增大,节理接触界面刚度越小则增加幅度越明显,当接近临界角时,透射系数TSC的增加幅度较大;反射系数RPC随着入射角度的增加而增大,而反射系数RSC逐渐降低;在入射角接近临界角的情况下,反射系数RPC迅速增加,而反射系数RSC下降幅度较小,并且这种现象随着节理接触界面刚度减小而愈加明显。

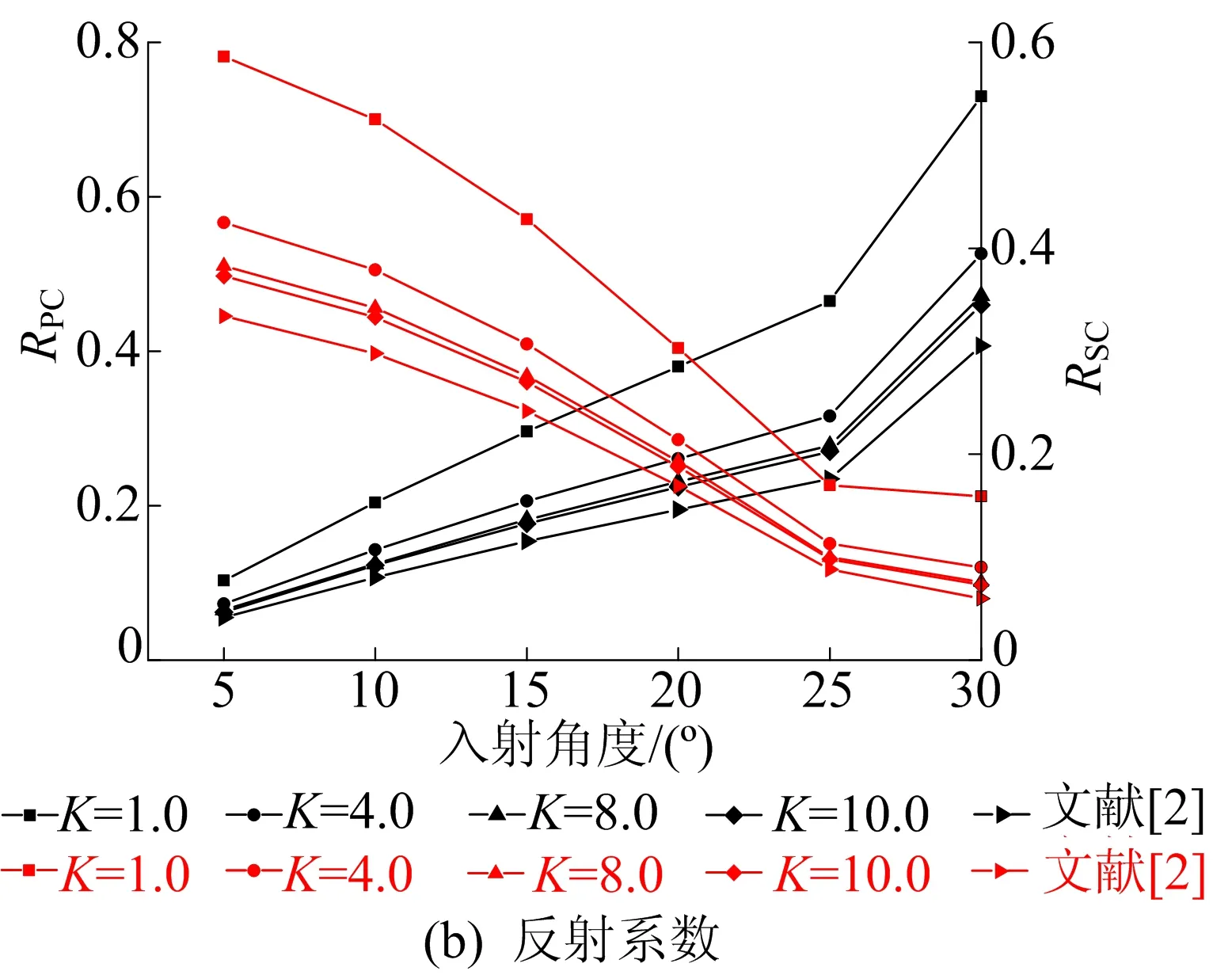
图10 S波在不同入射角度下透射与反射系数变化曲线

4 充填节理法向与切向力学特性

依据应力均匀性的假设,可通过节理两侧的质点速度推导出节理处的应力与位移。根据相同的方法,当节理厚度较小时,可将充填节理等效为位移不连续面模型,如图11所示。采用充填节理两侧的质点速度即可反推出不连续面的应力-位移力学特性,该力学特性同时考虑了节理接触界面与充填材料的共同变形。

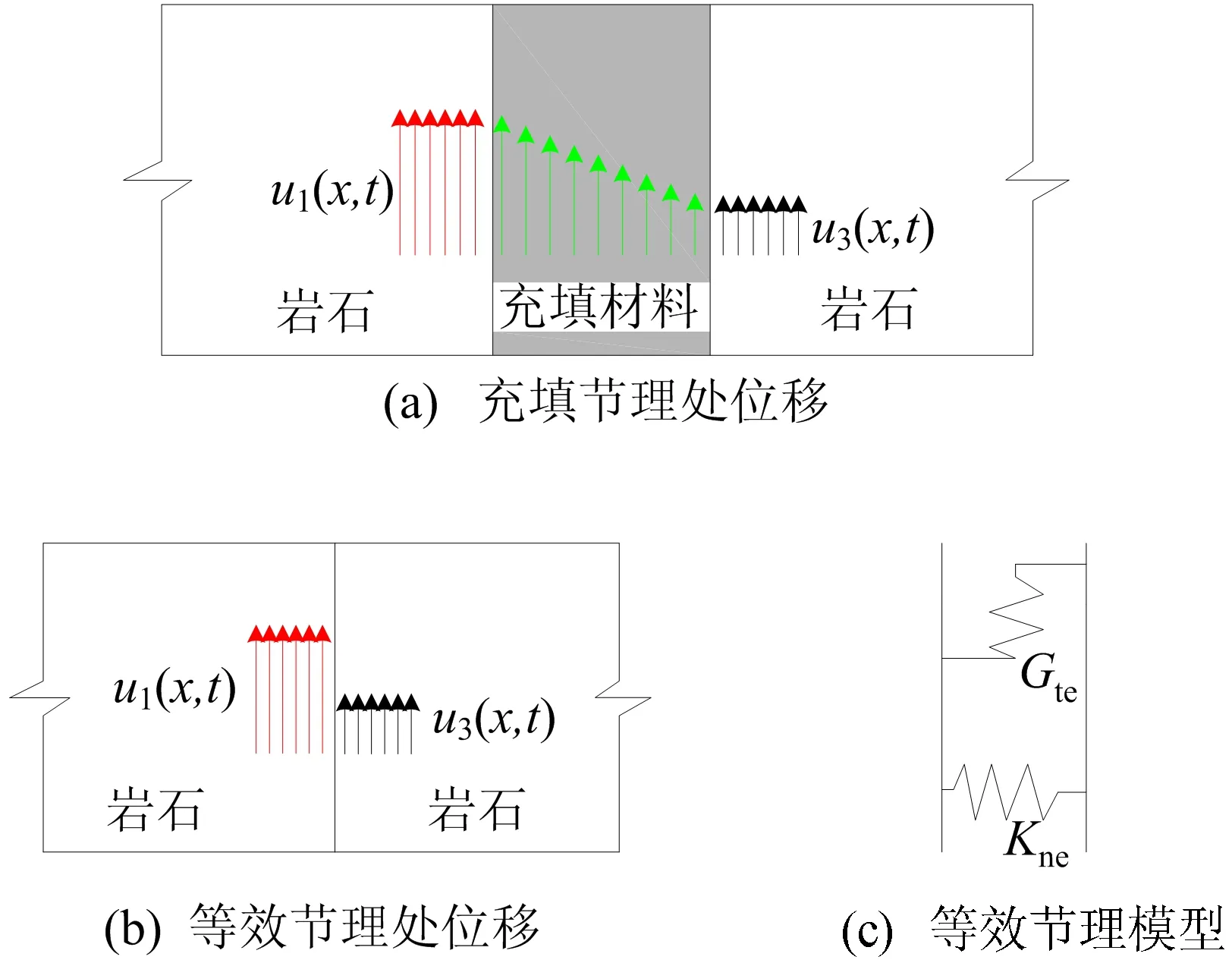
图11 充填节理与等效节理模型

4.1 接触界面刚度的影响

当P波法向入射充填节理时,法向应力与闭合量[2]分别为:

(16)

(17)

其中,Er为岩石的弹性模量。S波法向入射充填节理时,切向应力与闭合量[2]的表达式为:

(18)

(19)

其中,Gr为岩石的剪切模量。

通过(16)～(19)式可得出充填节理处应力与闭合量的关系,计算过程中入射波频率f=100 Hz,充填节理厚度为8 mm。应力与节理闭合量的关系曲线如图12所示。由图12可知:充填节理的法向与切向闭合量均随着应力的增加而增加,呈现出较强的线性关系;随着节理接触界面刚度的增加,应力与节理闭合量关系的斜率逐渐增大;当节理接触界面连续时,应力与节理闭合量关系的斜率达到最大值。

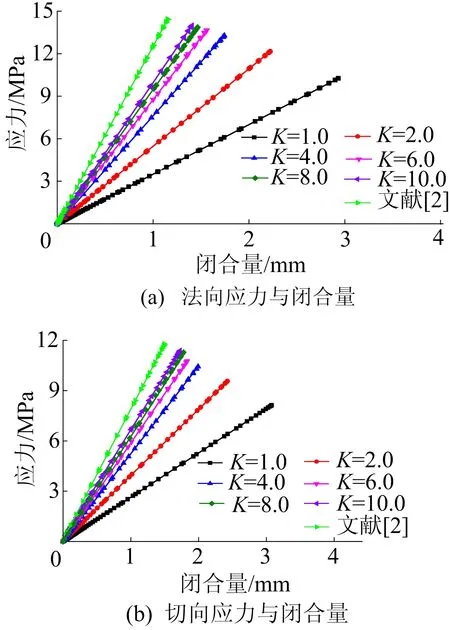
图12 应力与节理闭合量的关系曲线

4.2 节理厚度的影响

为了更好地描述充填节理的法向与切向力学特性,在考虑节理接触界面与充填材料的共同变形下,将法向应力与节理法向闭合量关系的线性斜率定义为等效法向刚度Kne,切向应力与节理切向闭合量的线性斜率定义为等效切向刚度Gte。不同节理接触界面刚度下Kne、Gte与节理厚度的关系如图13所示。

从图13可以看出:Kne与Gte均随着节理厚度的增加而降低;随着节理厚度的增加,当节理接触界面刚度较小时,Kne与Gte的降低幅度较小;当节理接触界面刚度较大时,Kne与Gte的下降幅度较大。例如:当节理厚度为4、20 mm时,K=10.0下的Kne分别为13.60、3.46 GPa,Gte分别为9.04、2.24 GPa,下降幅度分别为74%、75%;而K=4.0下的Kne分别为9.55、3.14 GPa,Gte分别为6.75、2.01 GPa,Kne与Gte的下降幅度分别为67%、35%。

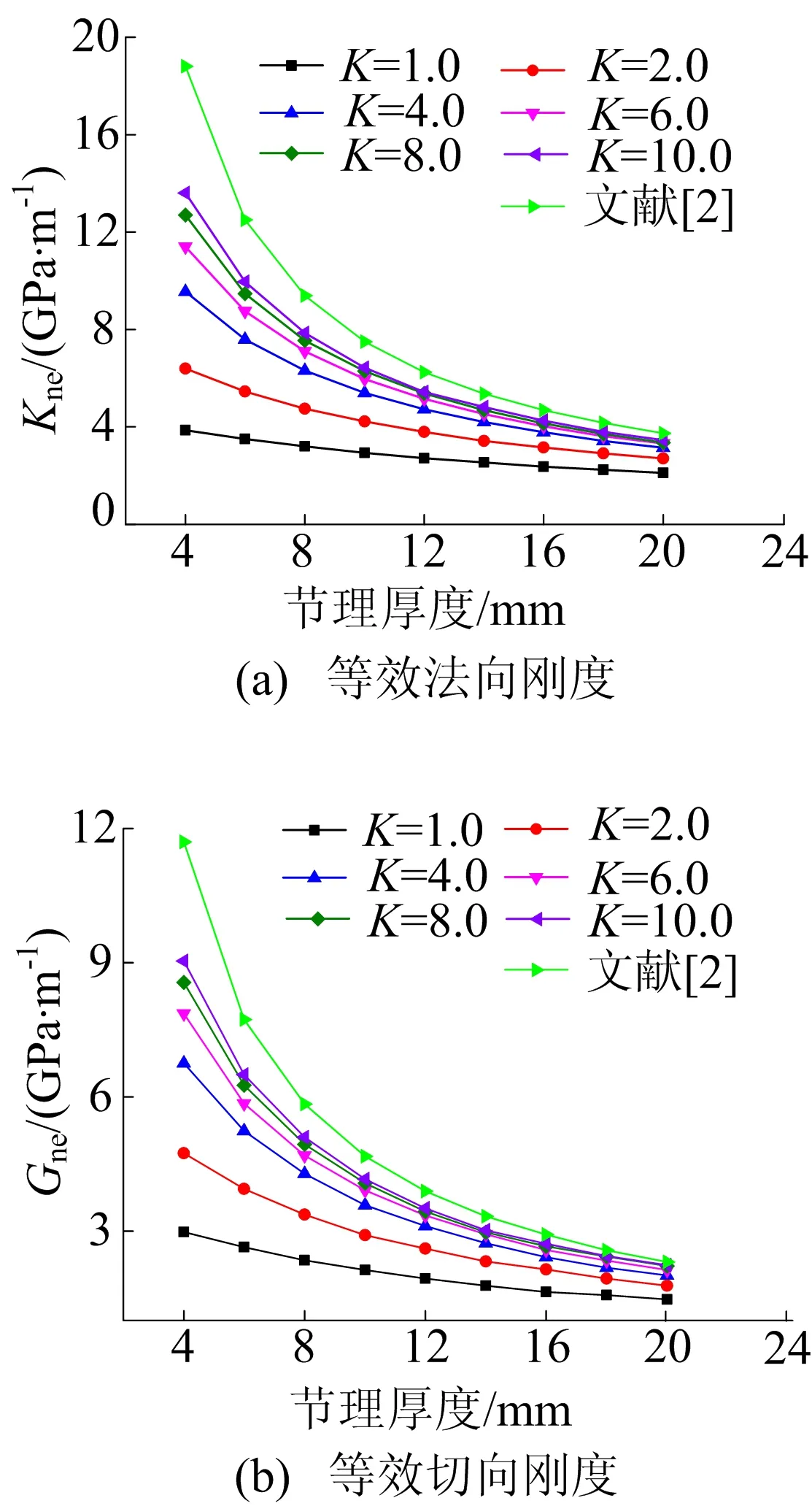
图13 不同节理厚度下等效刚度变化曲线

不同节理厚度下Kne、Gte与无量纲刚度系数K的关系如图14所示。

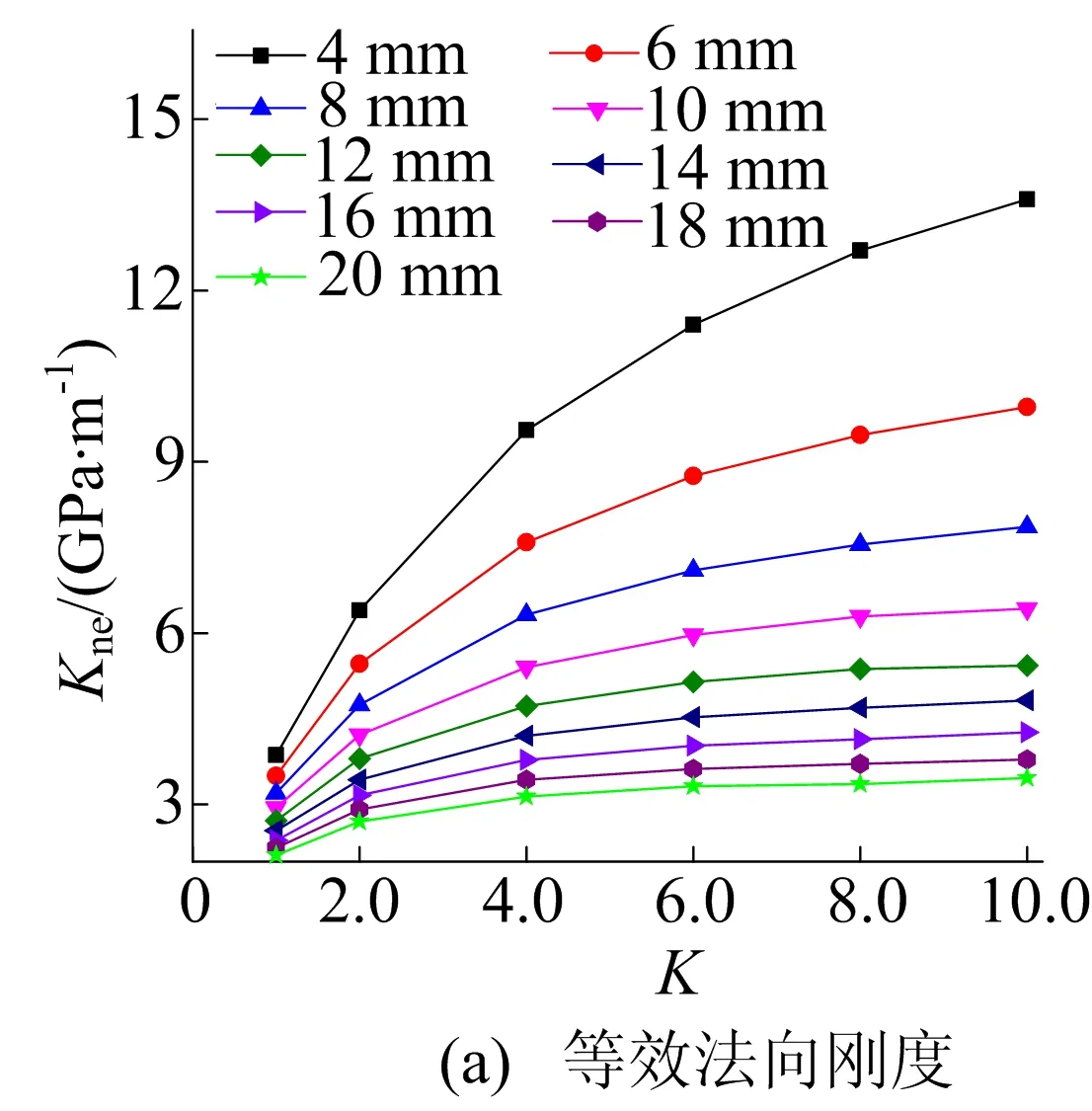
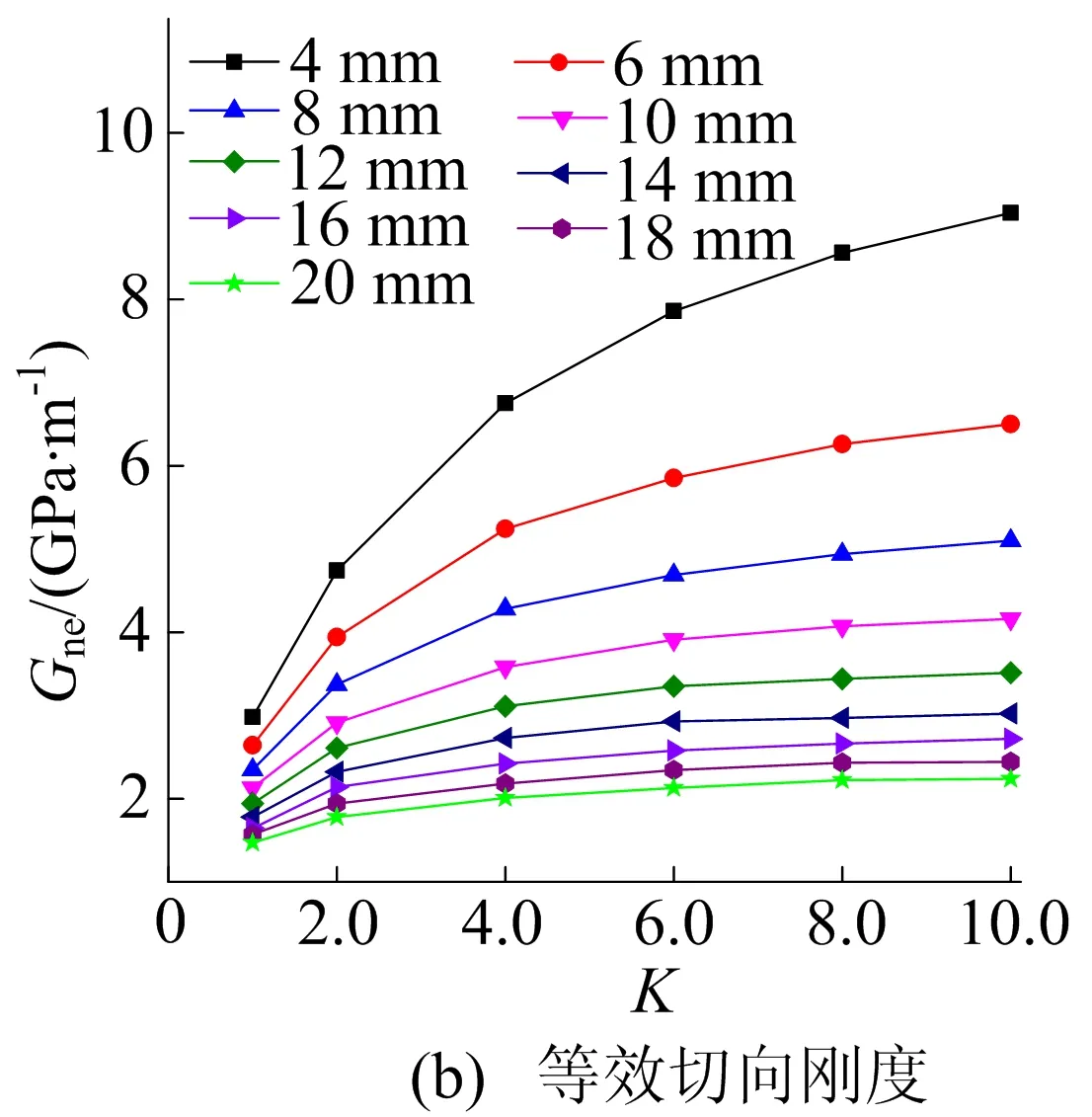
图14 不同节理接触界面刚度下等效刚度变化曲线

由图14可知:当节理厚度相同时,Kne和Gte均随着节理接触界面刚度的增加而增大;节理厚度越小,节理接触界面刚度对Kne与Gte的影响越明显;随着节理厚度的增加,节理接触界面刚度的影响逐渐降低,Kne与Gte的增加幅值明显降低。

这是因为充填节理一般由软弱材料填充,当节理厚度较大时,节理变形主要由充填材料变形引起,其对应力波的传播规律影响较大。因此,在节理厚度较大的情况下,随着节理接触界面刚度的增加,Kne和Gte的增加幅度较不明显。

5 结 论

本文考虑了节理接触界面与充填材料的共同变形,推导了P波和S波在充填节理处的波动方程,并进一步探讨了充填节理法向与切向力学特性的变化规律,主要得出以下结论:

(1) 通过将本文波动方程结果与文献[2]理论所得结果进行对比分析,验证了本文方法的可行性。在分析应力波法向与斜入射充填节理的力学行为时,本文方法显示出较高的精度。

(2) 节理接触界面刚度、节理厚度及入射角度均对应力波在充填节理处的传播规律产生影响。在相同节理厚度与应力波入射角度下,透射系数随着节理接触面刚度的增大而增大,反射系数则逐渐降低。

(3) 基于应力均匀性假设,得出充填节理法向与切向力学特性变化规律,发现等效法向与切向刚度均随着节理接触面刚度的增大而增大,但随节理厚度的增加呈降低趋势。