基于Hoek-Brown 强度准则的采场边坡岩体力学参数计算方法

曾少波，张 涛

在露天采场边坡工程中，岩体力学参数的确定对边坡稳定性评估和工程设计具有重要意义。岩体的不均匀性、各向异性和不连续性导致其强度既不是岩石的强度，也不是结构面的强度，它是岩体强度和结构面强度的组合。在实际研究中，结构面的几何参数和结构面的抗剪强度通常只能通过现场测绘和室内测试获得，而岩体的力学参数可以通过对岩体进行室内测试获得。目前，要获得岩体的力学参数非常困难，通常要通过经验评估和在野外进行大量的直接剪切试验来获得。大规模的原位剪切试验是通过在研究区域内选择和制作合适的原位样品，并对样品进行原位剪切试验来获得岩体的强度参数。虽然原地剪切试验可以获得岩体的强度参数，但这种方法的缺点是成本高，样品制作困难，试验周期长，不能测试大量的样品，试验数据的分散性大。此外，该方法只能在某些方向进行测试，在一些高陡坡地区，没有合适的测试场地。因此，原位直接剪切试验方法对岩体的实用性和适用性都很低。为了快速估算岩体的力学参数，Hoek—Brown 经验准则被工程界和学术界普遍接受。

Hoek—Brown 经验准则将岩体质量指数的确定与岩体强度参数的确定分开，从地质现场调查中估计岩体质量指数，从经验公式中描述岩体强度标准的特征，最后Hoek 通过确定岩体质量指数与经验强度准则之间的关系将两者结合起来。该方法被广泛用于隧道稳定性分析、边坡稳定性分析和地基承载力计算。

1 Hoek—Brown强度准则

实验室中制备的矿（岩）样品，虽然采自现场，但样品是一块完整性较好的岩块，不含或极少含有天然岩体所特有的软弱结构面，不能完全代表天然岩体的力学特性，因此，由实验室测得的力学参数需要按一定比例折减，才能应用于天然岩体中。

从理论上研究岩石和岩体的力学参数之间的关系是一个较难的课题，许多岩石力学工作者正在进行这方面的研究。通常人们大多是根据自己的工程经验或借鉴其它资料进行参数的折减，这样做无疑带有很大的随意性，影响后续分析结果的正确性、合理性，而Hoek—Brown 经验方程是比较好的、也是较流行的岩体—岩石力学关系确定方法。

Hoek 和Brown 根据岩体性质的理论与实践经验，用试验法导出了岩块和岩体破坏时主应力之间的关系为：

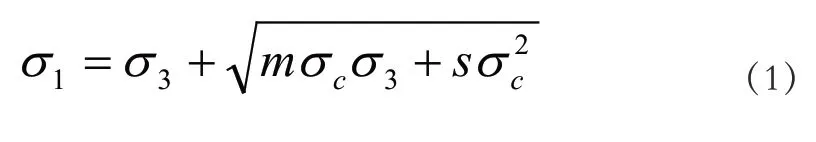
式中，1σ为破坏时的最大主应力；3σ为作用在岩石试样上的最小主应力；cσ为岩块的单轴抗压强度；m、s 均为岩体材料常数，取决于岩体性质。

此后，在工程应用中，H-B 准则不断得到改进并逐渐完善。2002 年，E.Hoek 对历年来的H—B 准则进行了详细而全面的审视，并对m，s，a 和地质强度指标GSI（geological strength index）的关系进行了重新定义，并提出了一个新的参数D 来处理爆破损伤和应力松弛。改进后的广义Hoek—Brown 强度准则可表示为：

其中

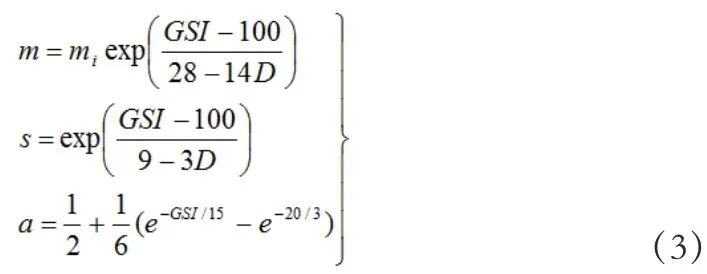
对于GSI ＞25 的岩体：a=0.5

对于 GSI ≤25 的岩体：a=0.65－GIS/200

式中：D 为岩体扰动参数，主要考虑爆破破坏和应力松驰对节理岩体的扰动程度，取值为0 ～1，对于未受扰动岩体，取D=0，对于严重扰动岩体，D=1；mi 为组成岩体的完整岩块的Hoek—Brown 常数，反映岩石的软硬程度；s 反映岩体破碎程度。

当用Hoek—Brown 准则估计节理化岩体强度与力学参数时，需用3 个基本参数：

（1）组成岩体的完整岩块的单轴抗压强度σc；（2）组成岩体的完整岩块的Hoek—Brown 常数mi；（3）岩体的地质强度指标GSI。

1.1 mi 的确定

mi可以通过室内岩石力学试验结果以及表1 来确定。把σ3=－σt和σ1=0 代 入Hoek—Brown 经 验 准 则，这里因为是完整岩块，因此s=1。由此公式，可以得到：

表1 完整岩体质量和经验常数之间关系表

1.2 岩体扰动程度D 值的确定

露天矿边坡通常是在不断地爆破采矿过程中形成的，直至开采结束，露天矿闭坑。爆破震动在岩体中产生的惯性力，使潜滑体的下滑力增大，抗滑力减小。在长期爆破震动荷载作用下，边坡岩体中具有弹、塑性性状的结构面将产生不可逆累计变形，裂隙扩展，并产生新的爆破裂隙。爆破是一种快速开挖方法，在爆破动荷载作用下，边坡中的初始应力迅速释放，岩体松动。据统计，爆破前后结构面的粘聚力c 值可降低40 ～60%，摩擦角φ降低10 ～15%。爆破震动分析表明，因此而造成边坡稳定系数降低30%是可能的。不适当的爆破对岩体强度降低的影响则更大。爆破是一长期作用过程，从而使边坡稳定系数的降低具有明显的时间效应。

根据现场围岩节理状况、岩体开挖扰动程度以及相关参考文献，确定英安岩D=0.85、流纹岩D=0.82、V1矿D=0.9、V2矿D=0.9。

1.3 GSI 的确定

GSI 为地质强度指标，是由Hoek、Kaiser 和Brown 于1995年建立，用来估计不同地质条件下的岩体强度。GSI 根据岩体所处的地质环境、岩体结构特性和表面特性来确定。但以往在岩体结构的描述或岩体结构的形态描述中缺乏定量化，难以准确确定岩体的GSI 值。为使其描述定量化，引入岩体质量RMR 分级法定量确定岩体质量等级。根据Z.T.Bieniawski 研究认为，修正后的RMR 指标值与GSI 值具有等效关系，确定修正后的RMR 指标值，即得出GSI 值。

RMR分级方法是采用多因素得分，然后求其代数和（RMR值）来评价岩体质量。参与评分的6 因素是：岩石单轴抗压强度、岩石质量指标RQD、节理间距、节理性状、地下水状态和结构面产状对边坡工程的影响。在1989 年的修正版中，不但对评分标准进行了修正，而且对第4 项因素进行了详细分解，即节理性状包括：节理长度、张开度、粗糙度、充填物性质和厚度以及风化程度。

表2 各岩性的D 及mi 值

2 岩体力学参数的确定

2.1 岩体变形模量

变形模量是描述岩体变形特性的重要参数，可通过现场荷载试验精确确定。但由于荷载试验周期长、费用高，一般只在重要的或大型工程中采用。因此，在岩体质量评价和大量试验资料的基础上，建立岩体分类指标与变形模量之间的关系，是快速、经济地估算岩体变形模量的重要手段和途径。

（1）E.Hoek 等建议岩体变形模量Em可用下式进行估算：

式中：岩体变形模量单位为GPa。

（2）利用量化RMR 系统和E.Hock 和M.S.Diederichs 的最新计算公式来进行岩体变形模量的取值：

式中：Ei—室内力学试验岩块的变形模量；

D—为岩体的扰动程度。

在RMR 与Em之间的诸多关系中，式（5）和式（6）已被工程界广泛采用，普遍认为其估算结果比较接近工程实际。哈秋瓴、张永兴等人根据三峡工程花岗岩岩体在现存条件下的RMR 指标，采用式（5）计算的变形模量，与现场原位试验测试结果比较一致。贵州工业大学宋建波教授曾对西南工学院新图书馆岩基的变形模量进行研究，估算结果也与勘察资料提供数据基本吻合。这从国内应用效果方面，侧面说明以式（5）和式（6）综合估算变形模量的方法是适用可行的。

本次采场边坡岩体变形模量Em取其上述两种公式的平均值。

2.2 岩体抗剪强度

莫尔强度曲线可用下式确定：破裂面上的正应力σ 和剪应力τ 为：

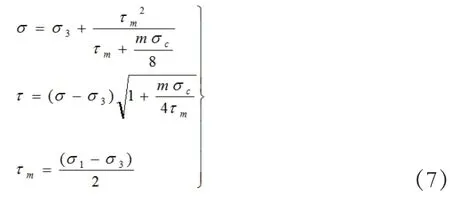
将相应的σ1和σ3代入式（7）就能在τ-σ 平面上得到莫尔包络线上σ 与τ 的关系点坐标。即可得出n 个参数点（τi， σi）。然后对这些参数点（τi， σi）数据进行回归处理确定出岩体抗剪强度参数。在运用Hoek-Brown 法原理计算岩体抗剪强度参数时，关键是选择σ3的范围，其最好范围：0＜σ3＜0.25σc。在本报告中选取σ3从0，1，2，3，……逐渐增大到0.25σc。由于岩体的抗剪强度、尤其是扰动岩体的抗剪强度多为非线性关系，故Hoek 提出了非线性关系式：

式中：A，B 为待定常数。改写上述方程，则变换为：式 中：y=lnτ/σc，x=ln（σ/σc－ T） ，a=B，b=lnA，

常数A 与B 可由最小二乘法线性回归确定：

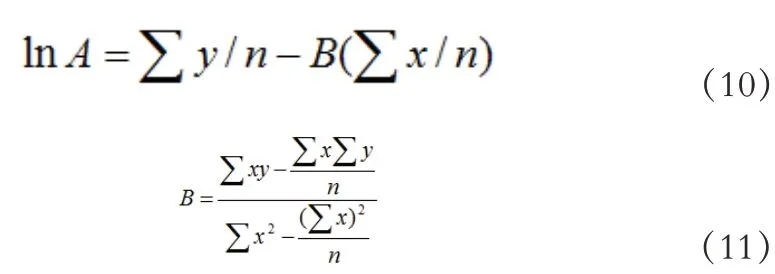
拟合相关系数：

由式（9）可知，当σ=0 时，τ=Cm，则岩体的粘聚力为

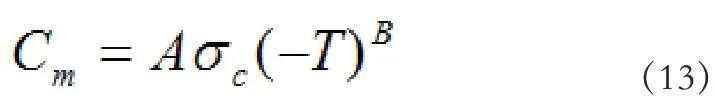
而在任一σi时非线性莫尔包络线的切线角即内摩擦角可由式（8）求导得：

为了表征岩体非线性破坏的总体或平均内摩擦角φm，采用下式：

3 岩体单轴抗压和抗拉强度

根据莫尔—库伦强度曲线以及图1 所示的几何关系可得：

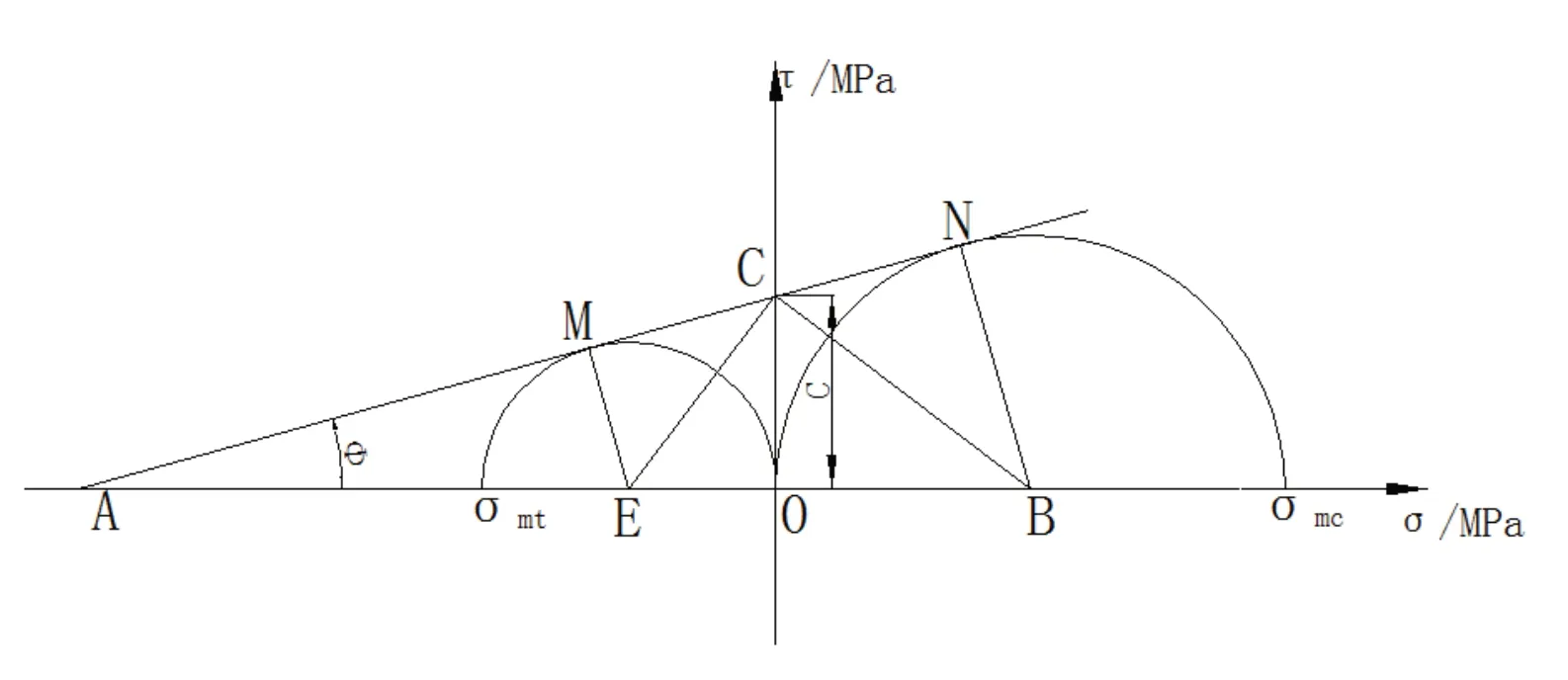
图1 莫尔圆与强度曲线的的几何关系图

（1）岩体单轴抗压强度

（2）岩体单轴抗拉强度

所以岩体的单轴抗压强度和抗拉强度：

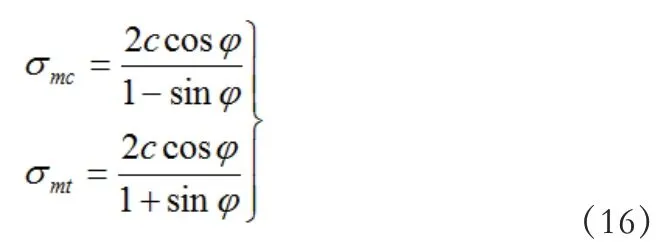
基础数据见表3，由表3 的岩体质量分级结果，根据式（5—9）～（5—20）计算出的岩体力学参数见表4 所示。

表3 基础数据

表4 岩体力学参数结果

4 岩体力学参数计算结果

由于岩体物理力学性质的非均质、各向异性的内在变化，以及外部因素的影响，给岩体力学参数的确定带来很多不确定性。为此，课题组采用了点荷载试验和室内岩土力学试验对大平掌铜矿岩体力学参数进行研究。结合2011 年《云南思茅山水铜业有限公司大平掌铜矿露天开采高边坡参数优化及边坡稳定性研究》报告中确定的岩体力学参数，结果汇总后见表5。

表5 岩体力学参数结果表

从表5 可以看出，英安岩和流纹岩基于点荷载试验所得出的岩体力学参数较低，强风化英安岩基于岩土力学试验所得的岩体力学参数相差不大。分析其原因，主要是点荷载试验对试验样品要求不高，样品数量较多，加之岩石物理力学性质的非均质性和各向异性，因此，所得出岩体力学参数波动范围较大，因此用平均值来代替其力学参数，所得结果偏低。综合考虑，最后确定的某采场边坡的岩体力学参数结果见表6。

表6 计算的岩体力学参数表

5 结论

（1）对岩石力学参数折减后得到岩体力学参数，并综合考虑点荷载试验、岩土力学试验可得到采场边坡研究的岩体力学参数。

（2）使用 Hoek Brown 岩体强度准则，结合岩石室内试验，估算岩体强度参数，对工程设计参数选取有一定参考意义。

（3）本文通过理论计算和室内试验，从侧面说明该参数选取的方法，对岩体力学参数选取有一定的借鉴。