基于频率响应特性的汽车操纵稳定性分析
张丽霞,郑超艺,潘福全,张文彩,刘家琪
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
操纵稳定性是现代汽车高速驾驶的“生命线”。随着汽车工业的发展,汽车的操纵稳定性已经成为企业在汽车研发时考虑的重要性能因素。Zhang等[1]基于二自由度车辆模型,研究正弦波输入条件下平衡点和相平面轨迹的变化。结果表明,相平面分析可以很好地用于分析车辆的操纵稳定性。Flavio等[2]讨论了两种不同的方法,一种是数值方法(相平面),另一种是图形方法(处理图)。数值模型表示完整的四轮车,图形模型表示自行车,分析质心纵向位置、轮胎侧偏刚度对车辆稳定性的影响。Shi等[3]基于车辆转向动力学理论,针对前轮角阶跃输入,在不同车速条件下,对车辆的横摆角速度等状态变量响应进行仿真分析,得到三种车速下状态变量在时域内的响应曲线。文献[4-5]基于汽车二自由度操纵稳定性模型,设计开发相应的控制算法,采用时域分析方法仿真分析汽车的操纵稳定性和控制器的鲁棒性。Hussein等[6]为了有效提高车辆的操纵稳定性、安全性和乘坐舒适性,提出一种协调控制策略,基于双移线和J型弯两种关键的驾驶工况,通过时域分析方法对车辆的操纵稳定性进行仿真分析。田萌健等[7]提出轮边底盘系统设计方案,对悬架的刚度、阻尼及零部件结构进行设计,考虑汽车的侧向动力学稳定性,基于时域分析仿真验证了设计的轮边底盘结构能够提高汽车的操纵稳定性。唐中华等[8]基于传递路径分析法建立了车辆虚拟传递路径分析模型,采用频率分析方法预测车内声学振动响应,得出在38 Hz处驾驶员右耳声压达到最大值以及在59 Hz处驾驶员座椅导轨振动处于较大峰值。李杰等[9]应用MATLAB软件开发了军用车辆随机振动分析软件,基于频率响应曲线,对采用虚拟激励法的军用汽车进行随机振动分析,结果表明此方法是简便且有效的。索明何等[10]为了验证某新型汽车蓄电池支架是否满足设计要求,基于频率分析方法对该蓄电池支架进行强度分析与优化设计,并通过整车道路耐久试验,结果表明所设计的蓄电池支架的优化方案满足要求。尽管人们为改善汽车的操纵稳定性做了大量研究,但现有的研究往往采用时域分析的方法研究不同车辆参数和控制策略对汽车操稳性的影响,或是采用频率响应方法对车辆的噪声振动和结构强度进行分析,目前没有基于频率响应函数和频率响应模型对汽车操纵稳定性进行分析的研究。采用频率响应方法对操纵稳定性进行分析,能够反映驾驶员以不同频率转动方向盘时,汽车横摆角速度和质心侧偏角的失真程度,更好地反映汽车的操纵稳定性。
本研究基于MATLAB/Simulink软件,采用频域分析方法,建立横摆角速度和质心侧偏角的频率响应数学模型和Simulink模型,对模型进行稳定性、动态响应和准确性分析。基于频率响应函数和频率响应模型,通过车辆转角脉冲响应的Bode图分析不同车速、载荷和前后轮胎侧偏刚度对汽车操纵稳定性的影响,为车辆设计初期的参数设计提供参考,对实车操纵稳定性实验具有一定的指导意义。
1 建立二自由度汽车数学模型
1.1 二自由度汽车模型的微分方程
建立数学模型过程中,以前轮转角作为输入,忽略转向系统传动比的影响;假设车体垂向的位移、俯仰角和侧倾角为零,忽略悬架系统的影响;汽车的纵向速度为常量[11]。将汽车简化成只有侧向运动和横摆运动两个自由度的线性定常系统。
令汽车的质心和车辆坐标系的原点重合,如图1所示。由图1计算可知二自由度汽车运动微分方程:

图1 二自由度汽车模型
(1)

1.2 横摆角速度的频率响应函数
将前轮角脉冲作为系统输入,汽车的横摆角速度作为输出,则运动微分方程为:
(2)
其中:M=m×Iz×u;h=-m×(a2×k1+b2×k2)-Iz×(k1+k2);c=m×u×(a×k1-b×k2)+(L2×k1×k2/u);b1=-m×u×a×k1;b0=L×k1×k2。
式(2)是横摆角速度强迫振动微分方程,通常写作:
(3)
其中,ωn=c/M,ζ=h/2ωn×M,B1=b1/M,B0=b0/M,ωn称为系统自然圆频率,ζ称为系统的阻尼比。
设系统输入和输出的时间函数分别为δ(t)和ωr(t),其傅里叶变换为:
(4)
对式(3)进行傅里叶变换,得到系统的横摆角速度频率响应函数:
(5)
则横摆角速度幅频特性为:
(6)
横摆角速度的相频特性为:
(7)
横摆角速度频率响应函数还可以表示为输出和输入幅值比的模和相角差乘积的形式:
(8)
1.3 质心侧偏角的频率响应函数
将前轮角脉冲作为系统输入,汽车的质心侧偏角作为响应输出,则运动微分方程为:
(9)
其中:b3=k1×Iz;b2=(m×u×a×k1)+(b×L×k1×k2/u)。
式(9)是质心侧偏角强迫振动微分方程,通常写作:
(10)
其中:B3=b3/M;B2=b2/M,
设系统输入和输出的时间函分别为δ(t)和β(t),其傅里叶变换为:
(11)
对式(10)进行傅里叶变换,得到系统的质心侧偏角频率响应函数:
(12)
则质心侧偏角幅频特性为:
(13)
质心侧偏角的相频特性为:
(14)
2 建立MATLAB/Simulink汽车模型
根据上述频率响应函数,基于MATLAB/Simulink软件建立汽车操纵稳定性仿真模型如图2所示。汽车模型的参数如表1所示[12],利用以上仿真参数在MATLAB里编写频率响应函数,运行Simulink模型,得到横摆角速度伯德图与质心侧偏角伯德图,通过仿真试验分析不同工况下横摆角速度和质心侧偏角对汽车操纵稳定性的影响。

表1 汽车仿真参数

图2 汽车操纵稳定性仿真模型
3 评价汽车操纵稳定性的频域参数
汽车横摆角速度的频率响应特性反映汽车的横向稳定性,质心侧偏角的频率响应特性直接影响驾驶员的驾驶感受,因此,将这两项评价指标作为系统的输出量[13]。
为了使汽车具有较好的操纵稳定性,对频率响应特性的要求是:
1)输入频率为零时的零频值即横摆角速度稳态增益应该适当大一些,其大小反映了汽车转向灵敏度;
2)谐振频率应该高一些,谐振频率越高,汽车的操纵稳定性越好;
3)幅频特性曲线应该尽量平坦些,谐振峰值应该较小,避免响应幅值失真程度或超调量过大。谐振峰值和零频值的比值越大,说明系统的相角裕度和阻尼比越小,超调量越大,达到稳态的调节时间也越长;
4)带宽频率应该高些,即通频带应该宽些,以保证响应的反应速度和高频段反应,但是带宽频率也不能太高,否则会降低系统对高频干扰的抵抗能力,通常规定增益降至零频值的0.707倍处的频率为带宽频率;
5)相频特性在通频带内的相位超前角和滞后角都应该小一些,以保证汽车在不同频率的方向盘转角输入下有快速灵活的响应[14]。
4 方向盘角脉冲试验仿真分析
4.1 频率响应特性稳定性分析
根轨迹法是三大分析矫正方法之一,是传递函数的极点在s平面相应变化所描绘出来的轨迹[15]。根轨迹法的优点是直观、形象,可以根据极点的分布情况判断系统的稳定性,适于研究当系统中某一参数变化时的系统性能变化趋势。由根轨迹法可知,当系统的根轨迹全部位于虚轴左侧的时候,系统是稳定的[16]。由图3可知:汽车二自由度模型的频域响应函数的根轨迹全部位于虚轴的左侧,可以判断系统是稳定的。

图3 系统的根轨迹图
4.2 频率特性动态响应分析
以汽车的横摆角速度频率特性动态响应为例分析汽车操纵稳定性,系统的对数幅相特性如图4所示。
由图4可知:当频率为零时,系统的横摆角速度增益(零频值)为4.36 dB,汽车具有一定的转向灵敏度;随着输入频率的增大,幅相特性曲线接近一条水平线,当输入频率达到4.68 rad/s时增益曲线出现峰值,汽车达到共振状态,此时的输入频率为系统的谐振频率,谐振频率对应的横摆角速度增益(谐振峰值)为19.87 dB;随着输入频率继续增大,横摆角速度增益逐渐下降,当增益下降到稳态增益的0.707倍时,即增益下降到3.06 dB时,输入频率为18.47 rad/s,称此频率为带宽频率。系统应该具有较高的带宽频率,以保证响应的反应速度和高频段反应。从相频特性曲线可知:在汽车方向盘转动频率较低时,相位角差值为3°左右,当快速转动方向盘时,相位角滞后20°左右,汽车横摆角速度滞后于方向盘转角,失真度较低,汽车具有较好的操纵稳定性。

图4 横摆角速度伯德图
4.3 频率响应特性精度分析
稳态误差是系统重要的稳态性能指标,是对系统控制精度的度量[17]。影响稳态误差的因素有:①系统自身的结构参数;②系统的外作用类型(控制量、扰动量及作用点);③系统的外作用形式(阶跃信号、斜坡信号或加速度信号等)。
对于稳定的系统,研究稳态误差才有意义,所以计算稳态误差以系统稳定为前提[18]。4.1节的分析已证明系统是稳定的,本节只讨论系统的原理性误差,不考虑由于非线性等因素引起的误差。由式(2)可知系统的开环传递函数为:
(15)
整理为尾一标准型:
(16)
由式(16)可知:系统的开环增益为K=b0/c=1.65,系统的型别为零型,由静态误差系数法可知系统的稳态误差为0.38,符合系统对精度的要求。
5 不同工况下汽车操纵稳定性频域分析
5.1 不同车速下的幅相特性对比
为了分析车速对汽车操纵稳定性的影响,保持系统的其他参数不变,改变汽车的纵向行驶速度,通过MATLAB/Simulink仿真分析,得出汽车在行驶速度分别为u1=60 km/h,u2=80 km/h,u3=100 km/h工况下的横摆角速度频率幅相特性曲线和质心侧偏角频率幅相特性曲线,如图5和图6所示,对比分析纵向行驶速度对汽车操纵稳定性的影响。
由图5可知:当汽车行驶速度下降25%,横摆角速度幅值曲线的零频值增加47.8%,汽车具有较高的转向灵敏度;汽车行驶速度越高,系统的横摆角速度幅频特性曲线的峰值越高,车速下降25%,横摆角速度谐振峰值与零频值的比值减小39.9%,此时幅频特性曲线越平坦,汽车动态响应的幅值失真度和超调量越小,汽车达到稳态状态的调节时间越短,系统的动态响应性能越好,具有较好的操纵稳定性;由相频特性曲线可知,当以缓慢的速度转动方向盘时,系统的横摆角速度相位差几乎为零,随着输入频率的增加,输出相位角与输入相位角的差值越来越大。输入达到谐振频率时,相位角差值最大。当车速由80 km/h减小到60 km/h,相位角的差值由36°减小到24°,此时系统在不同速度的方向盘转角下具有快速灵活的响应。由图6可知:当输入频率较低时,汽车的质心侧偏角几乎为零;达到谐振频率时,车速越低,系统的质心侧偏角越小,汽车的纵向车速降低25%时,质心侧偏角谐振峰值与零频值的比值降低45.3%,输出的幅值失真度越小,并且系统有较小的相角差。降低车速可以改善系统在不同频率输入下的动态响应,提高汽车的操纵稳定性能。
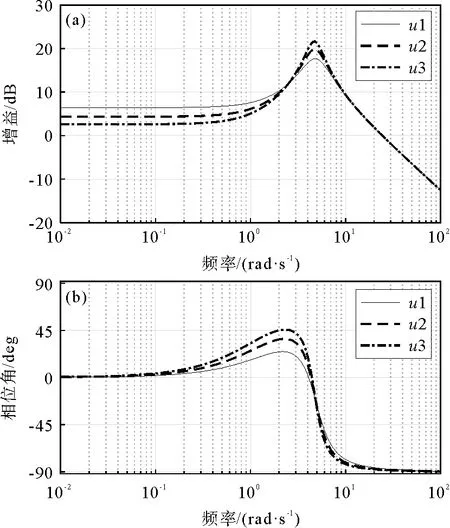
图5 不同车速下横摆角速度的伯德图

图6 不同车速下质心侧偏角的伯德图
5.2 不同载荷下的幅相特性对比
为了对比分析载荷对操纵稳定性的影响,保持其他参数不变,改变载荷参数,通过仿真,得出汽车载荷为m1=1 500 kg,m2=1 800 kg,m3=2 100 kg的工况下的横摆角速度频率幅相特性曲线和质心侧偏角频率幅相特性曲线,如图7和图8所示,对比分析汽车载荷对操纵稳定性的影响。

图7 不同载荷下横摆角速度的伯德图
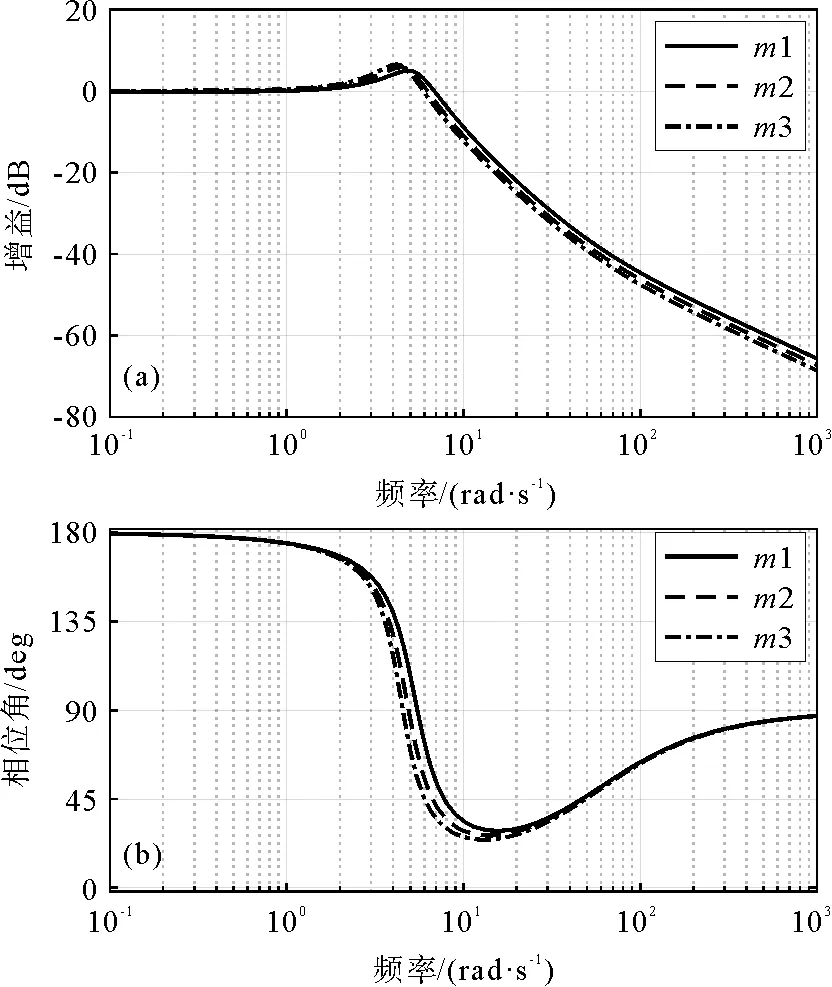
图8 不同载荷下质心侧偏角的伯德图
由图7可知:汽车载荷越小,系统横摆角速度对数幅频响应的零频值越高,汽车载荷下降16.7%,横摆角速度的稳态增益增加33.9%,汽车具有较好的转向灵敏度;当载荷下降16.7%,横摆角速度的谐振峰值与零频值的比值减小24.8%,此时幅频特性曲线越平坦,汽车动态响应的幅值失真度和超调量越小,系统的动态响应性能越好;当汽车载重量下降16.7%,横摆角速度的谐振频率增高10.1%,并且横摆角速度的带宽频率增加8.7%,系统有较快的响应速度和高频段反应稳定性;由横摆角速度相频特性曲线可知,当以缓慢的速度转动方向盘时,系统的横摆角速度相位差几乎为零,随着输入频率的增加,输出相位角与输入相位角的差值越来越大,达到谐振频率时,相位角差值最大,载荷由1 800 kg减小到1 500 kg,相位角的差值由37°减小到32°,此时系统在不同速度的方向盘转角下具有快速灵活的响应。由图8可知:当输入频率较低时,汽车的质心侧偏角几乎为零,达到谐振频率时,载荷越小系统的质心侧偏角越小,汽车载荷降低16.7%时,质心侧偏角的谐振峰值降低14.2%,输出的幅值失真度越小。降低汽车的载荷可以改善系统以不同速度转动方向盘时的动态响应,提高汽车的操纵稳定性能。
5.3 不同前轮侧偏刚度下的幅相特性对比
为了对比分析汽车前轮侧偏刚度对操纵稳定性的影响,保持系统的其他参数不变,改变侧偏刚度,通过仿真,得出汽车前轮在侧偏刚度为kf1=52 618 N/rad,kf2=62 618 N/rad,kf3=72 618 N/rad的工况下的横摆角速度频率幅相特性曲线和质心侧偏角频率幅相特性曲线,如图9和图10所示,对比分析汽车前轮侧偏刚度对操纵稳定性的影响。

图9 不同前轮侧偏刚度下横摆角速度的伯德图

图10 不同前轮侧偏刚度下质心侧偏角的伯德图
由图9可知:汽车前轮的侧偏刚度越大,横摆角速度幅频特性曲线的稳态增益越高,侧偏刚度增加38%时零频值增加334%,系统具有较好的转向灵敏度,此时汽车的不足转向趋势减小;随着输入的方向盘转动频率增高至谐振频率,增益出现最高值即达到谐振峰值,当前轮的侧偏刚度减小27.5%时,横摆角速度的谐振频率增加21.3%。汽车对高频的输入有较好的操纵稳定性;在输入频率的高频段区间,前轮侧偏刚度越小幅频特性曲线的趋势越陡且越低,根据频率响应的三频段理论可知前轮侧偏刚度较小的汽车对高频干扰的抵抗能力比较强。由相频特性曲线可知:当前轮侧偏刚度由52 618增大到72 618 N/rad时,横摆角速度输出相角与输入相角的差值由40°减小到32°,汽车在不同频率的方向盘转角输入下有快速灵活的响应。由图10可知:质心侧偏角增益的零频值随着前轮轮胎侧偏刚度的增大而增大;谐振频率随着侧偏刚度的减小而增加,前轮侧偏刚度越小汽车中频段附近的操纵稳定性越好;侧偏刚度越小的汽车高频段幅频响应曲线越低陡,具有较好的抵抗外界高频干扰的能力。由质心侧偏角相频特性可知较高的前轮侧偏刚度具有较小的相位角差值。在低频段,较大的前轮侧偏刚度具有较好的转向灵敏度,在中频段和高频段,较小的前轮侧偏刚度具有较好的操纵稳定性。
5.4 不同后轮侧偏刚度下的幅相特性对比
为了对比分析后轮侧偏刚度对汽车操纵稳定性的影响,保持系统的其他参数不变,改变侧偏刚度,通过仿真,得出汽车前轮在侧偏刚度为kr1=90 185 N/rad,kr2=110 185 N/rad,kr3=130 185 N/rad工况下的横摆角速度频率幅相特性曲线和质心侧偏角频率幅相特性曲线,如图11和图12所示,对比分析后轮侧偏刚度对操纵稳定性的影响。

图11 不同后轮侧偏刚度下横摆角速度的伯德图
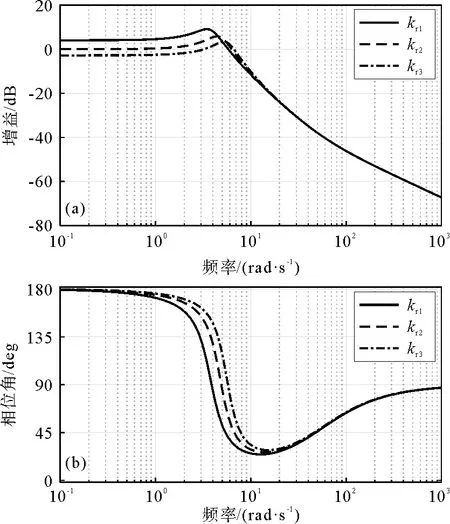
图12 不同后轮侧偏刚度下质心侧偏角的伯德图
由图11可知,汽车后轮的侧偏刚度越小,横摆角速度幅频特性曲线的稳态增益越高,侧偏刚度减小30%时零频值增加52%,系统具有较好的转向灵敏度,此时汽车的不足转向趋势减小;随着输入的方向盘转动频率增高至谐振频率,增益出现最高值即达到谐振峰值,当后轮轮胎的侧偏刚度增大44%时,横摆角速度的谐振频率增加27.9%。汽车对高频输入有较好的操纵稳定性。由相频特性曲线可知,当后轮侧偏刚度由90 185 N/rad增大到130 185 N/rad时,横摆角速度输出相角与输入相角的差值由29deg减小到24deg,汽车在不同频率的方向盘转角输入下有快速灵活的响应。由图12可知,质心侧偏角增益的零频值随着后轮轮胎侧偏刚度的减小而增大;谐振频率随着侧偏刚度的增大而增加,后轮侧偏刚度越大汽车中高频段附近的操纵稳定性越好。由质心侧偏角相频特性可知较高的后轮侧偏刚度具有较大的相位角差值。在低频段,较小的后轮侧偏刚度具有较好的转向灵敏度,在中频段和高频段,较大的后轮侧偏刚度具有较好的操纵稳定性。
6 结论
汽车角脉冲输入频率响应特性能反应汽车动态响应的灵敏度-超调量-调节时间和转向灵活性,是一种有效的汽车操纵稳定性分析方法,可以为车辆设计初期的参数设计提供参考,缩短汽车设计和实验周期。本研究基于MATLAB/Simulink软件,建立了横摆角速度和质心侧偏角的频率响应函数和模型,分析不同车速、载荷和前后轮胎侧偏刚度对汽车操纵稳定性的影响,可以得出以下结论:
1)降低汽车的行驶速度可以改善系统在不同频率输入下的动态响应,提高汽车的操纵稳定性能;
2)降低汽车的载荷可以改善系统以不同速度转动方向盘时的动态响应,提高汽车的操纵稳定性能;
3)当输入的方向盘转角频率较低时,较大的前轮侧偏刚度具有较好的转向灵敏度,当输入的方向盘转角频率较高时,较小的前轮侧偏刚度具有较好的操纵稳定性;
4)当输入的方向盘转角频率较低时,较小的后轮侧偏刚度具有较好的转向灵敏度,当输入的方向盘转角频率较高时,较大的后轮侧偏刚度具有较好的操纵稳定性。

