一种GNSS广播星历轨道实时改正方法
刘 路,郭金运,周茂盛,刘 新,纪 兵
(1.山东科技大学 测绘与空间信息学院,山东 青岛 266590;2.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉430079;3.海军工程大学 导航工程系,湖北 武汉 430033)
全球卫星导航系统(global navigation satellite system, GNSS)因可提供全天候服务、高精度点位信息等优势,被广泛应用在导航定位等领域[1-2]。在应用GNSS时,卫星星历不可或缺且卫星星历的误差会对定位与导航精度带来直接影响[3]。当前GNSS卫星星历主要可分为2种:广播星历和精密星历,前者因其实时性、易获取的特点被广泛应用在实时导航定位中[4],但其精度低的特点限制了实时导航与定位精度的提高;后者虽然精度高,但有较大的滞后性,主要应用于事后科学研究。因此,如何进一步提高广播星历的精度成为GNSS导航定位系统在实时应用领域亟待解决的重要问题之一。
基于国际GNSS服务(International GNSS Service,IGS)组织的精密星历,国内外学者对GNSS广播星历的轨道和时钟做了许多精度评估方面的研究[3-17]。Warren等[5]首次基于精密星历研究了全球定位系统(global positioning system,GPS)广播星历卫星轨道的精度演变;叶有龙等[6]对比研究了GPSBlock IIA和GPS Block IIF卫星广播星历的精度,得到了Block IIF卫星广播星历精度明显优于Block IIA卫星广播星历精度的结论。伴随着国外其他系统的逐步建设,众多学者基于IGS精密星历对全球导航卫星系统(Global navigation satellite system,GLONASS)、伽利略卫星导航系统(Galileo satellite navigation system,Galileo)、北斗卫星导航系统(BeiDou navigation satellite system,BDS)等系统的广播星历精度进行研究。郭际明等[7]研究了短期的GLONASS广播星历轨道误差和钟误差,得到当时该导航系统广播星历整体精度信息(优于4.5 m)。韩德强等[8]分析了30 d(年积日330~359 d)的Galileo广播星历的空间信号测距误差,结果表明Galileo广播星历的精度优于1.0 m,具备完全运行能力(full operational capability,FOC)卫星的广播星历精度与在轨验证(in orbit valition,IOV)卫星的广播星历精度相当。赵立都等[9]通过分析2015年3月1日—28日BDS广播星历误差,给出当时3种北斗卫星的广播星历精度信息。此外,基于上述方法对各系统广播星历进行精度分析时发现轨道3个方向(径向、切向、法向)的误差存在周期规律[3-12],其中最显著的周期是卫星轨道运行周期。这为基于数学方法分析其轨道误差序列的规律性、区分轨道误差序列的有用信息与噪声、建立相应的实时改正方法提供了可能性。
奇异频谱分析(singular spectrum analysis,SSA)作为一种数字信号处理技术[18],不仅能从时间序列中提取蕴含的非线性趋势,而且能够识别和强化周期信号[19-20];结合加权相关分析(w-correlation)可以选择合适阶次对序列重构和外推[21],非常适合对具有周期震荡的时间序列数据和对此类时间序列数据进行预测[22]。
因此,本研究从数学方法分析广播星历轨道误差序列(由广播星历及对应的精密星历构建的轨道误差序列)规律的角度出发,在最终与快速精密星历的时间延迟分别为12~18 d和17~18 h、时延较长前提下,提出利用广播星历及对应的超快速精密星历(观测部分)构建轨道误差序列,建立一种基于SSA的GNSS广播星历轨道实时改正方法,以提高现阶段广播星历的轨道精度。
1 数据与处理方法
1.1 数据
本研究采用的GNSS广播星历及超快速精密星历均来自IGS全球数据中心之一的地壳动力学数据信息系统(crustal dynamics data information system,CDDIS)。其中广播星历是RINEX 3.03版本的p文件,这种格式的星历文件包含多个系统(如GPS, GLONASS, BDS等)的GNSS广播星历。需要注意的是,不同系统的广播星历的采样间隔及给出的轨道参数形式有所差别,如GPS广播星历给出的是间隔为2 h的开普勒轨道参数,而GLONASS广播星历给出的是间隔15 min的轨道位置和速度。超快速精密星历文件为SP3 c版本,当前只包含GPS卫星的星历,间隔为15 min,时间总长度为48 h(其中前24 h的星历是实测数据解算的,时延在3~9 h,精度较高;后24 h的星历是预测的,相比于前24 h的数据精度低),每6 h更新一次。因此,本研究以GPS卫星为例进行实验验证分析。
1.2 方法
具体数据处理流程如图1所示。

图1 数据处理流程图
首先,利用两种GNSS星历得到轨道误差序列,进行预处理;然后,利用SSA分解重构得到有用信息(趋势项、周期项、准周期项)和噪声信息;最后,利用SSA预测轨道误差序列的有用信息作为广播星历轨道的改正数实时改正广播星历轨道。
1.2.1 数据预处理
广播星历文件中的星历数据有时会出现错误与缺失的问题,所得到的轨道误差序列也难免存在粗差或缺失,需要进行数据预处理。本研究数据预处理包括对广播星历及精密星历数据质量的控制、轨道误差序列的粗差剔除和缺失数据的迭代插值。
具体处理方法如下:
1)对于广播星历,剔除标记为不健康卫星的轨道参数;剔除同一颗卫星相邻两组轨道参数产生较大变化的轨道参数;
2)对于精密星历,剔除精度指数为0和指数较大卫星全天的位置坐标;剔除卫星在某一历元下出现0.000 000的位置坐标;
3)卫星轨道各个方向误差如果大于10 m,则作为粗差剔除[12];
4)利用SSA迭代插值对因星历数据缺失,或粗差剔除造成的不完整轨道误差时间序列进行补全。SSA迭代插值的具体方法将在1.2.3节中做详细介绍。
1.2.2 基于SSA的轨道误差序列分解与重构
使用SSA是为了把轨道误差时间序列分解成一系列独立序列,包括噪声、周期或准周期和趋势项。其步骤如下。
1)构建时滞矩阵
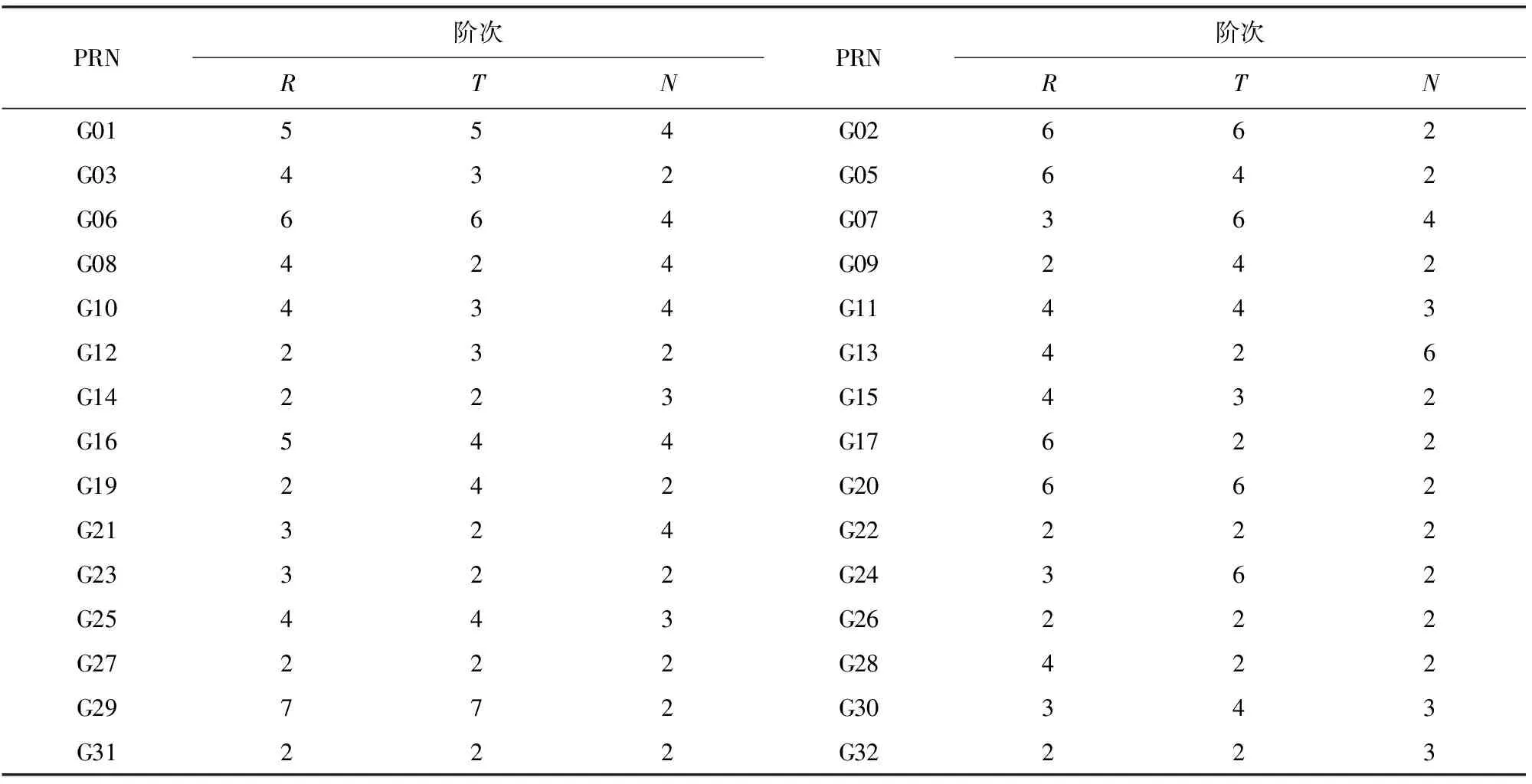
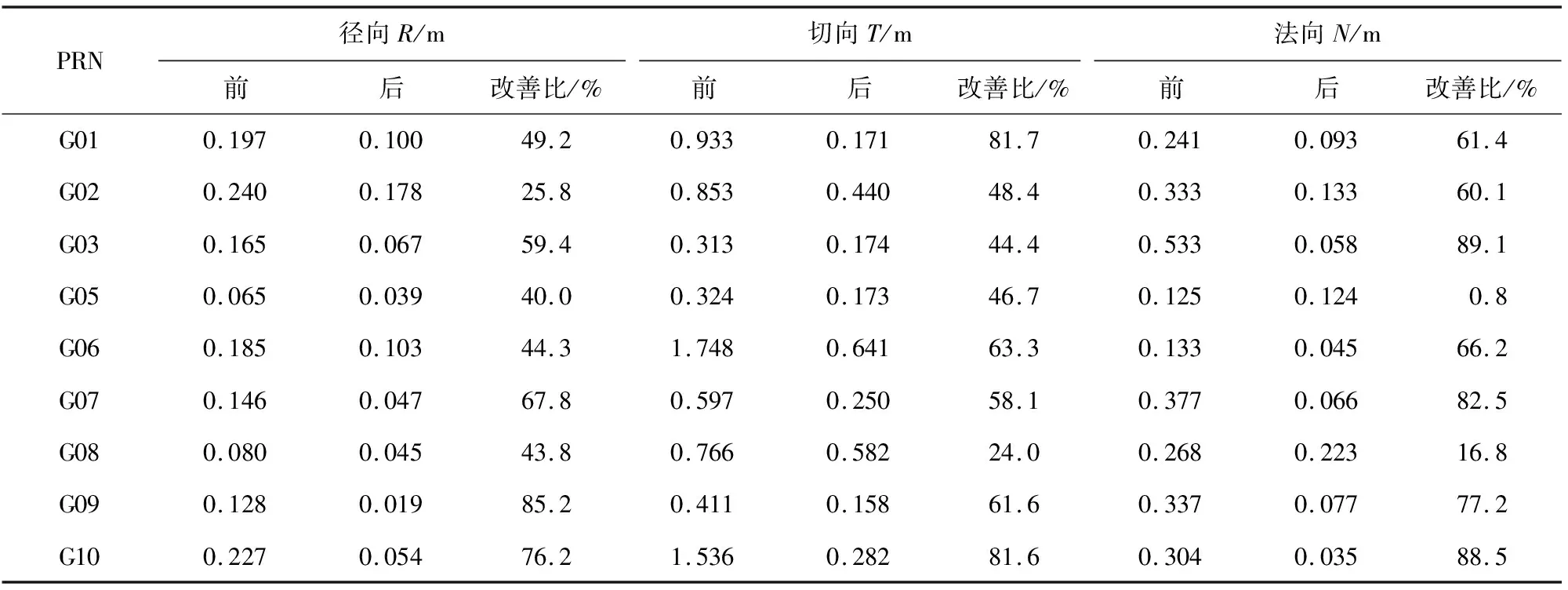
对于序列长度为N的轨道误差序列x1,x2,…,xN,设窗口长度为整数M(1 (1) 其中xi(1≤i≤N)代表原始轨道误差序列中的第i个元素。时滞矩阵X的每一行、每一列都是原始轨道误差序列的子序列。 2)奇异值分解 令Tx=XXT,得到滞后协方差阵 (2) X=X1+X2+…+Xd。 (3) 3)对角平均化 将初等矩阵Xr通过对角平均化转换为长度为N的多个重建向量(reconstruction component,RC),原始轨道误差序列为所有RC之和。令矩阵Z=Xr,Z通过对角平均化可得到时间序列z1,z2,…,zN。对角平均化的具体公式为: (4) 其中,M*=min(M,K),K*=max(M,K)。 (5) 1.2.3 轨道误差序列有用信息SSA预测 利用SSA迭代插值[23-24]预测时间序列的具体过程如下: 1)假设原始轨道误差序列的长度为N,设置轨道误差序列的预测长度为l,预测部分先用0值填充,则可以得到长度为N+l轨道误差序列,对此轨道误差序列进行中心化处理; 生物滤池:这里的生物一般指的是厌氧生物,氧化池与滤池在结构上比较相似,主要不同为生物滤池是封闭状态的。生物滤池还有低成本、低消耗,操作简单、便捷等特点,不需较多人力成本,因此在农村生活污水处理方面是比较常用的方法之一。 2)SSA分解中心化处理后的轨道误差序列,SSA分解后轨道误差序列预测位置的数据用第1个RC(记为RC1)中的最后l个数据替代,之后再进行SSA分解,循环此过程,直到2次预测数据差值的均方根(root mean squre,RMS)小于0.001 m; 3)添加RC2预测数据,RC1和RC2线性叠加,重复步骤2),构建新的轨道误差预测数据; 4)根据各RC的贡献率和w-correlation对RC进行相关性分析,选择适量的RC重复上述过程,直至得到较为理想的预测结果。 使用SSA对广播星历轨道误差序列进行预测,首先需要确定窗口长度M和有用信息阶次。为说明如何解决这2个问题,采用2018年1月20日—30日GPS广播星历及其对应超快速精密星历(观测部分)首先得到32颗在轨运行卫星中的30颗卫星的原始轨道误差序列(G04卫星没有数据,G18卫星数据缺失严重);然后预处理原始轨道误差序列,得到15 min间隔的完整轨道误差序列。 对于窗口的选取,一般取1 有用信息阶次可以通过w-correlation对SSA分离出的RC进行相关性分析和各RC贡献率来确定,其中相关性分析能够判断各RC分离结果的好坏。对30颗卫星轨道误差序列进行SSA分解,计算前12阶RC的相关系数。图2给出G01卫星轨道误差序列SSA分解的前12阶RC的相关系数,以说明如何确定有用信息的阶次。 图2 G01卫星轨道误差SSA分解的前12阶RC相关系数 采用相同的方法确定其他29颗卫星广播星历轨道误差序列的有用信息阶次,结果如表1所示。 表1 每颗卫星轨道径向、切向、法向误差的有用信息的阶次 (6) 式中σi(i=R,T,N)为i方向所有卫星改正后的广播星历轨道减去对应的超快速广播星历轨道差值的均方根。其结果如图3所示。 图3 不同原始序列长度对应的整体三维轨道误差 由图3可知,对于广播星历轨道误差预测,原始序列长度并不是越长越好,当原始广播星历轨道误差序列长度为3 d时,对应整体三维轨道的误差值最小,即整体预测结果最好。因此,选取3 d为最佳原始序列的长度。 为评定该方法的可行性,以2018年1月28日—30日3 d的广播星历轨道误差序列为原始序列,M=96为窗口长度,对表1确定的每颗卫星轨道误差的有用信息阶次利用SSA进行预测,预测长度为6 h(2018年1月31日前6 h),预测结果作为广播星历轨道改正数。将经过预测值改正前后的广播星历轨道分别与对应的超快速精密星历的轨道作差,统计得到每颗卫星改正前后的轨道误差均方根,通过比较改正前后轨道误差均方根的大小来验证该方法的可行性。表2给出了SSA预测值改正前后每颗卫星广播星历轨道的精度及其改善比。 表2 SSA预测值改正前后每颗卫星广播星历轨道的精度及其改善比 从表2可以看出,用SSA对广播星历轨道误差有用信息的预测值去改正广播星历轨道,卫星在轨道径向上的最大正改善比为85.2%,最小正改善比为3%,4颗卫星(G15、G21、G23、G32)出现负改善比,占卫星总数的13.3%;卫星在轨道切向上的最大正改善比为92.2%,最小正改善比为9.8%,3颗卫星(G23、G26、G27)出现负改善比,占卫星总数的10%;卫星在轨道法向上最大正改善比为89.1%,最小正改善比为0.8%,2颗卫星(G24、G26)出现负改善比,占卫星总数的6.7%,且轨道法向整体改善效果最好。因此,从整体改善效果证明该方法是可行的。 少数卫星轨道的某些方向精度出现负改善比的原因是:一是个别在该时间段内广播星历轨道误差本身较小的卫星(如G15径向误差为厘米级),利用SSA预测只用了有限阶次,这会引入少许误差,所造成的负改善比仅仅是引入较小的轨道误差,但这对整体改善效果影响较小;二是卫星出现轨道机动等事件时,会破坏轨道误差原本的周期性,导致利用SSA并不能很好地分解重构有用信息项并进行正确预测,这是卫星本身出现的事件所致,并不是方法缺陷。 本研究利用广播星历及对应的超快速精密星历(观测部分)构建轨道误差序列,建立一种基于SSA的GNSS广播星历轨道实时改正方法。以GPS为例,实验探讨了轨道误差SSA预测窗口大小、有用信息的阶次选取及最佳原始序列长度确定等问题;最后实验验证了利用该方法可以改善GNSS广播星历轨道,提高GNSS广播星历的轨道精度。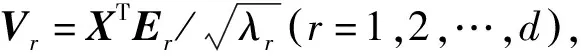
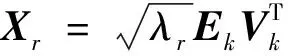

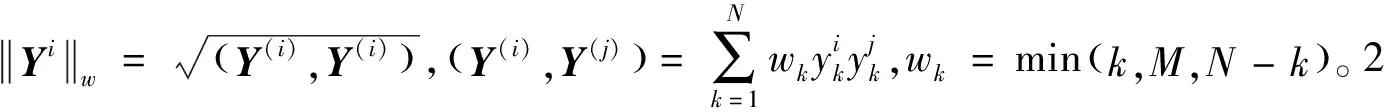
2 实验与分析
2.1 SSA预测窗口及有用信息阶次的确定


2.2 最佳原始序列长度的确定

2.3 基于SSA的轨道误差预测可行性验证
3 结论

