水沙流作用下粗糙度对圆柱体结构受力特性及冲蚀的影响

乔智威，刘 壮，张宪堂，张惠尧，李泽熹，李 丹

(1.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；2.山东科技大学 土木工程与建筑学院，山东 青岛 266590；3.山东高速青岛公路有限公司，山东 青岛 266114；4.山东科技大学 地球科学与工程学院，山东 青岛 266590)

当水流以一定速度绕过圆柱体结构时，随着流动的分离会出现卡门涡街现象，引发柱体在来流方向和垂直方向上出现作用力的周期变化。这种作用力能够引发结构物自身产生周期振动，当旋涡脱落的频率与圆柱体结构振动频率接近时，会导致结构物的损坏。而水流中含有的不同浓度沙粒更是增大了水流对结构物的损坏程度。桥梁作为跨越河流的常用手段，桥桩、桥墩等圆柱体结构长期受到水流的冲蚀作用，对其使用寿命造成严重影响。因此研究绕流时柱体的受力特性及水沙流对柱体的冲蚀，对工程设计非常重要[1-2]。

水体绕流对柱体受力特性产生的影响，既与流体本身的特性有关，也受结构物尺寸的影响。Zdravkovich等[3-5]通过实验发现，随着雷诺数的改变，绕流时柱体的受力状态也会发生改变；崔维征等[6-8]发现结构体的尺寸改变会影响其绕流的动力特性；胡彬等[9-11]通过对不同直径的圆柱进行数值模拟，发现改变圆柱直径的大小会影响柱体的受力特性；申彦兵等[12]通过改变柱体粗糙度，探究了粗糙度对圆柱绕流柱体受力特性的影响；王凯鹏等[13]发现来流条件、不同柱体的间距比都会对圆柱体上的受力产生影响。

柱体的粗糙度是影响柱体受力的一个重要因素，目前对水沙流的研究重点集中于冲蚀角[14-15]、颗粒直径[16-17]等因素对冲蚀的影响，尚未涉及柱体粗糙度对冲蚀影响的研究。本研究基于Fluent软件，采用剪切应力输运(shear stress transport, SST)k-ω湍流模型，针对含沙量较小的长江流域，研究不同含沙量水流作用下圆柱体的受力特性及冲蚀受粗糙度的影响。

1 数值方法

1.1 数学方程

假定流体黏性不可压缩，不考虑温度对流场的作用，忽略能量方程，仅考虑质量守恒和动量守恒方程：

(1)

(2)

式中，ui、uj分别为i、j方向的瞬时速度，p为压力，ρ为流体的密度，xi、xj分别为i、j方向的脉动速度，t为时间，υ为黏度系数。

1.2 参数的定义

阻力系数Cd、升力系数Cl是柱体所受阻力和升力经无量纲化后的结果，是定义绕流的主要特征参数。冲蚀率Rerosion是单位质量粒子对材料造成的质量磨损，是评价粒子对材料冲蚀程度的参数。

升力系数、阻力系数、冲蚀率的表达式分别为：

(3)

(4)

(5)

式中，ρ为流体密度，U为流体速度，D为流场中的圆柱的直径，Fd为圆柱所受的阻力，Fl为圆柱所受的升力，mp为颗粒质量，C(dp)为颗粒直径函数，α为颗粒对壁面的冲击角，f(α)为冲击角函数，v是颗粒相对壁面的速率，b(v)是相对速度函数。

利用Fluent软件，对圆柱壁面所受的力及冲蚀磨损量的结果进行监测，通过换算，得到Cd、Cl、Rerosion的具体数值。

2 计算模型的设置及验证

2.1 计算参数

圆柱直径D为1.0 m，水流速度为1.0 m/s，雷诺数Re=1.0×106，计算流场与圆柱的布置如图1所示。入口与圆柱中心的距离为10D，出口与圆柱中心的距离为15D，前后表面与圆柱中心的距离均为10D，圆柱展向高度的取值为πD。圆柱材料与C40混凝土相同，抗压强度取值为40 MPa，弹性模量为3.25×104MPa。

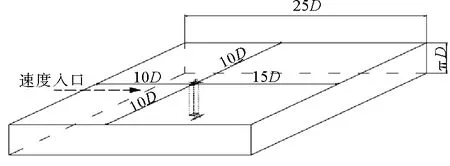
图1 三维数值计算区域

2.2 边界条件

计算流场的入口为速度入口，出口为自由流出，上下表面为周期性边界，前后表面为对称边界，时间步长设置为0.1 s，残差精度取10-5。

2.3 网格划分

利用ICEM CFD对网格进行划分。为了监测圆柱壁面附近的复杂流场变化，对壁面附近区域采用O型切分，加大网格密度。网格划分方式如图2所示，网格数量为2.8×106。

图2 网格划分方式示意图

2.4 模型验证

为确保结果的准确性，对选用的计算模型进行验算。验算时，为节约计算资源，柱体粗糙度取0、水流含沙量为0，其他条件与正常计算流场相同。由于阻力系数和升力系数曲线在前期具有随机性，只有在流场稳定之后才会具有周期平稳性，因此在流场稳定后，再对升力系数和阻力系数进行相应处理。

验算模型的升力系数在流场稳定后的曲线变化如图3所示。通过图3可发现，在流场稳定之后，升力系数会出现具有周期规律的上下波动，这与文献[18]的研究结果相符。

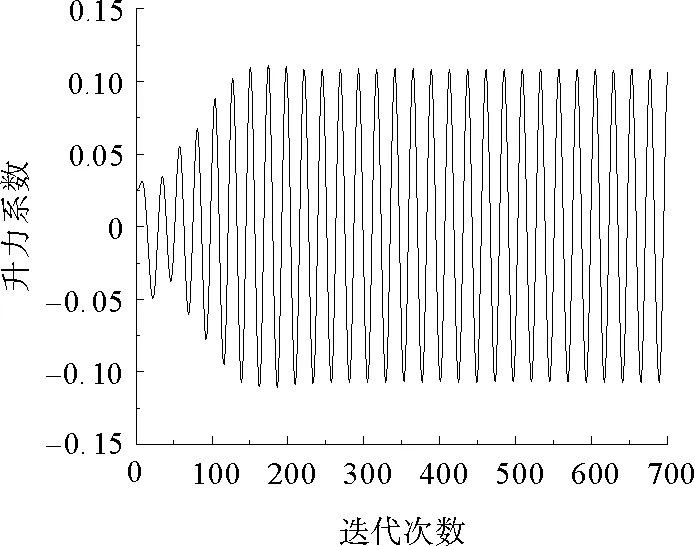
图3 稳定后的升力系数的迭代曲线

将阻力系数均值与相同雷诺数下之前学者的研究结果进行对比，结果如表1所示。通过表中的结果对比可知，数值模拟的结果与Pietro的试验结果以及其他学者的研究结论相吻合，验证了采用的模型对圆柱绕流模拟具有良好的预测精度。

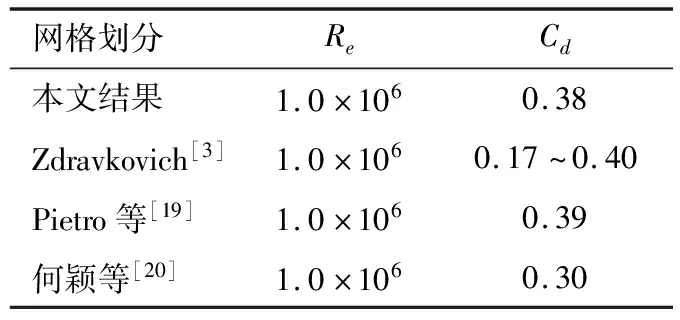
表1 阻力系数与其他文献的结果比较

3 结果与分析

3.1 阻力系数分析

通过观察阻力曲线的变化，发现待流场稳定后，阻力系数在某一固定值附近出现周期变化，呈现出相对稳定状态。求得平稳周期内阻力系数的平均值，得到不同含沙水流下平均阻力系数与柱体粗糙度间的变化曲线，如图4所示。

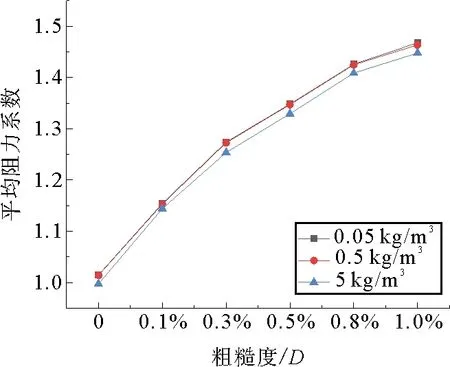
图4 不同粗糙度下的平均阻力系数

圆柱体结构在水流的作用下，平均阻力系数与柱体表面粗糙度的变化趋势受含沙量影响较小。当水流的含沙量为0.5和5 kg/m3时，平均阻力系数的变化趋势与含沙量0.05 kg/m3时的变化趋势大致相同，相同粗糙度下的平均阻力系数虽然在数值上有所下降，但其变化幅度最大仅为2%。这是因为当水流的速度一定时，含沙量由0.05 kg/m3改变至0.5 kg/m3，与由0.5 kg/m3改变至5 kg/m3相比，尽管后者的含沙量改变值在数值上较前者变化幅度更大，柱体上的阻力也出现了一个小幅度的改变，但与总体相比改变仍不明显，说明当水沙流的含沙量在0.05 kg/m3至5 kg/m3时，含沙量对柱体所受阻力的影响较小，结构体所受的阻力主要与流体的特性相关。从整体上看，当水流的含沙量相同时，柱体的平均阻力系数随着粗糙度的增大呈升高趋势，但其上升速率逐渐下降，且在粗糙度由0增大到0.1%D时，平均阻力系数的增长率最大，这与文献[21]所得结论一致。

3.2 升力系数分析

对不同粗糙度下的圆柱升力系数的变化进行分析，如图5所示。

在粗糙度相同的情况下，随着水流含沙量增大，柱体的升力系数逐渐增大，说明了柱体上的升力受水沙流含沙量的影响较大。从升力系数的最大值上看，当水流的含沙量由0.05增加到0.5 kg/m3时，柱体上的升力系数增大了15倍；而当水流的含沙量由0.5增大至5 kg/m3时，柱体上的升力系数仅增大了10倍；水流含沙量的增长率与柱体上的升力系数增长率不成正比关系，说明柱体所受的升力与水流的含沙量之间呈非线性关系。在水沙流的含沙量相同时，柱体的升力系数随着粗糙度的增大，呈现出先升高后降低，然后再回升的趋势，且3种含沙量下的圆柱升力系数的变化趋势呈现相同的增长规律，其升力系数的最大值均出现在柱体粗糙度为0.5%D的情况下，这说明了存在一个最佳粗糙度值[22]，当超过这个最佳粗糙度时，会在卡门涡街脱落时，对上表面的涡脱产生抑制作用，从而使得升力降低。

3.3 冲蚀率分析

对不同粗糙度的圆柱壁面受到含沙水流冲蚀时的磨损结果进行分析，绘制柱体冲蚀率的变化曲线，如图6所示。

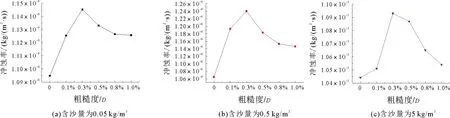
图6 壁面冲蚀率随粗糙度变化趋势

通过分析不同含沙量水流下粗糙度对圆柱壁面冲蚀率影响的变化趋势，对比含沙量由0.05增大至0.5 kg/m3和由0.5增大至5 kg/m3这两个阶段的情况发现，虽然二者的水流含沙量都扩大了10倍，但前者对圆柱壁面最大冲蚀率的改变量却达到了100倍，与后者的10倍相比，相差了1个数量级；这说明随着含沙量的不断增大，水沙流对圆柱壁面冲蚀破坏的增长速率会在前期急剧增大，而后逐渐减小。从整体上来看，在粗糙度相同的情况下，随着水流含沙量的增大，壁面冲蚀率也越大，这也与实际情况相符。在水沙流的含沙量相同时，圆柱的壁面冲蚀率随着柱体表面粗糙度的增大，呈现出先升高后降低的情况，且3种含沙量下的圆柱壁面冲蚀率的变化趋势呈现出相同的增长规律，其壁面冲蚀率的最大值都出现在柱体粗糙度为0.3%D的情况下；这是由于水流在与柱体的粗糙表面作用后，会产生一个伴生涡[23]进而提高水流对沙粒的搬运效率，当水流速度一定时，伴生涡的大小和强度在柱体粗糙度为0.3%D时达到最大，从而使得此时壁面冲蚀率最大。

4 结论

利用Fluent软件对水沙流下的圆形柱体进行了数值模拟，讨论了3种不同含沙量、5种不同柱体表面粗糙度对圆柱绕流及冲蚀的影响，得到以下结论：

1)平均阻力系数的变化受柱体表面粗糙度的影响较小，且在柱体表面粗糙度由0增大到0.1%D时，平均阻力系数的增长率最大。

2)在不同含沙量的水沙流作用下，升力系数的变化呈现出相同的规律，当柱体表面粗糙度为0.5%D时，升力系数达到该含沙量下的最大值。

3)当柱体表面粗糙度由0增大到0.3%D时，壁面冲蚀率逐渐增大，且在0.3%D时达到该含沙量的最大值；当柱体表面粗糙度由0.3%D增大到1.0%D时，壁面冲蚀率逐渐减小。