经纬仪测量系统的铅垂基准尺综合定向方法

刘尚国，赵少良，景 冬

(山东科技大学 测绘与空间信息学院，山东 青岛 266590)

经纬仪测量系统由2台或2台以上高精度经纬仪组成，基于空间角度前方交会原理实现三维坐标测量[1-2]。作为一种便携式、高精度的大尺寸空间坐标测量系统[3]，被广泛应用在航空航天、装备制造及大型工业设备安装检测等领域。

由于该系统的观测值只有方向值，故各测站空间位置标定必须借助定向测量来完成，包括相对定向和绝对定向。相对定向一般需要通过仪器间精确互瞄测量，确定经纬仪在连线方向的起始方向值[4]。而绝对定向则是确定系统测量的尺度基准，一般通过观测1根已知长度的基准尺完成[5]。

作为一种纯粹的三角法测量系统[6]，借助基准尺确定系统测量的尺度基准是绝对定向的基本方法。例如景冬等[7-8]提出的基于可整平基准尺的定向测量方法，潘廷耀等[9]、肖华杰等[10]提出的多基准尺联合标定技术，殷泽军等[11]提出的基于标准尺的基线反演求解算法等。吴卓昊等[12]研制的铟钢四面体结构校准装置提供6根基准杆，可实现常用工业测量系统现场精度的原位校准。

经纬仪测量系统定向测量的实质是确定各测站经纬仪的相对位置关系，若将各测站位置参数纳入统一平差模型中一并求解，则称为“综合定向”，其方法主要有光束法平差、六自由度测站三维网平差等[13-14]。而在相对狭小或受限的测量空间内，如玻璃生产线辊子姿态检测、矿井提升机形位检测等，受通视及现场条件的限制，基准尺只可铅垂放置。针对铅垂基准尺定向，文献[15]讨论了一种“垂直角视距法”实现综合定向。但是，该算法要求基准尺严格铅垂放置，在实际作业中难以实现。经实验测试，发现可基于“垂直角视距法”获取定向参数的初始值，考虑到基准尺近似铅垂放置的一般情况，依据附有条件的间接平差模型，实现经纬仪测量系统的综合定向，定向参数计算较为准确。

1 铅垂基准尺综合定向的理想模型

如图1，基准尺处于理想铅垂状态时，其端点1和2在水平面内的投影重叠为点P。A、B为2测站经纬仪的中心，为确定水平基线长度b及测站高差hAB，将长度为D的基准尺铅垂放置，分别从A、B测量其上、下2标志点1、2，测得垂直方向值分别为VA1、VA2、VB1、VB2。

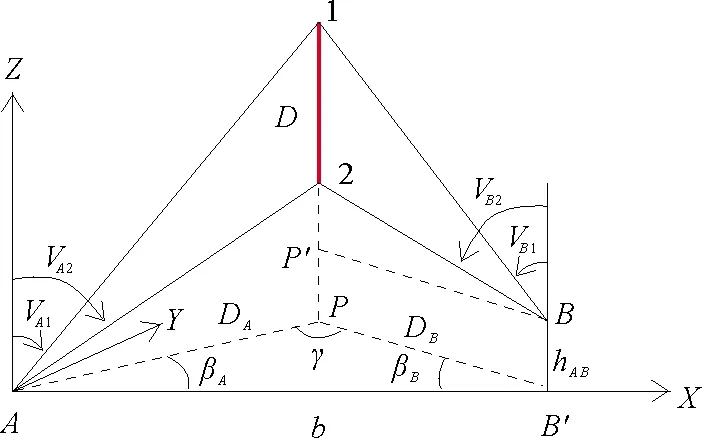
图1 铅垂基准尺综合定向的理想模型

2经纬仪交会线、基准尺及其投影线，在竖直面内构成4个直角三角形，即RtΔA1P、RtΔA2P、RtΔB1P′和RtΔB2P′，记经纬仪A、B至基准尺的水平距离(即“视距”)分别为DA和DB。分析铅垂直角边与基准尺D之间的几何关系，可得：

(1)

再分析直角三角形RtΔA2P和RtΔB2P′的铅垂直角边，可得高差

hAB=DAcotVA2-DBcotVB2。

(2)

根据余弦定理，可计算水平基线长度

(3)

其中，γ=180°-βA-βB。在相对定向系统误差ε1=-ε2=ε前提下，交会角γ的计算式为：

(4)

求出b后，根据正弦定理计算水平角βA、βB：

(5)

则相对定向的系统误差：

(6)

对互瞄观测值追加系统误差改正，解决了相对定向的问题。

2 综合定向实用模型及算法

2.1 综合定向的平差模型

由于基准尺很难严格铅垂放置，故其实际交会构形如图2所示。理想模型求出的定向参数可作为初始值。设待定的定向参数为基准尺2端点的三维坐标1(X1,Y1,Z1)、2(X2,Y2,Z2)以及水平基线长度b、两测站间高差h、互瞄方向观测值HAB和HBA，而观测量为水平方向值HA1、HA2、HB1、HB2和垂直方向值VA1、VA2、VB1、VB2。通过解析待定参数与观测量之间的函数关系，可列出观测方程：

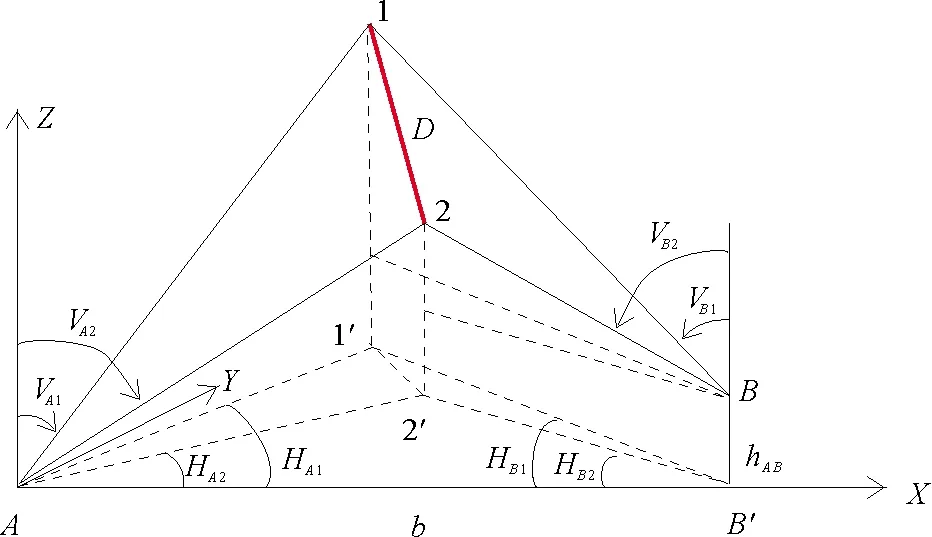
图2 铅垂基准尺的实际交会构形

(7)

同时，考虑到基准尺条件

(8)

可列出式(9)误差方程，适用附有限制条件的间接平差模型。

(9)

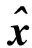
(10)

(11)

2.2 定向参数的解算

实际工作中，为确保综合定向参数解算的可靠性，需观测多根基准尺或将基准尺摆放多个位置。每观测1次基准尺，即可按式(7)～(11)列出8个观测方程和1个条件方程，而待定参数的个数增加6个。若基准尺摆放并观测n个位置，则观测方程个数、待定参数个数分别为9n和4+6n。

为求解待定参数，要求观测方程个数大于待定参数个数，故铅垂基准尺综合定向中，至少应将基准尺摆放并观测2个位置。此时，式(9)的维数为：

(12)

根据附有限制条件的间接平差原理，可得平差值为：

(13)

则观测值及待定参数为：

(14)

式中，L为观测值向量。

(15)

单位权中误差的估值为：

(16)

3 实验分析

3.1 铅垂基准尺定向的实验方案

采用由2台Leica M5100A电子经纬仪构成的Axyz经纬仪测量系统，进行基于铅垂基准尺的综合定向测量实验。如图3所示，为使观测方程个数大于待定参数个数，本次实验分别将基准尺放置于经纬仪基线的前后①、②、③等3个位置，借助垂球线安置基准尺处于近似铅垂状态。为确保测量成果的可靠性，同时测量P1～P8等8个定向点。

图3 铅垂基准尺综合定向测量实验

Leica Axyz经纬仪测量系统的定向测量算法基于光束法平差模型[4,17]，是一种公认、可靠的定向测量方法。在10 m范围内，其绝对定向所得水平基线b长度的误差可控制在±0.05 mm以内，故可将Axyz定向结果作为定向实验结果的评判标准。

将2经纬仪间的水平基线长度分别控制在2.5、5.0、7.5和10.0 m左右，共进行4组定向测量实验。定向解算时，为保证解算结果具有可对比性，使用同一组原始观测数据。相继采用光束法平差模型、铅垂基准尺综合定向理想模型、铅垂基准尺综合定向实用模型[18]，3种定向模型分别简记为Leica Axyz算法、PB_Ideal算法和PB_Practical算法。

3.2 定向参数的解算结果分析

3种定向模型均通过经纬仪间精确互瞄完成相对定向，故相对定向参数没有可比性，仅对比分析3类算法所求解的绝对定向参数，如表1所示。表中的Δb和Δh分别为铅垂基准尺综合定向解算的水平基线长度b、测站高差h相对于Leica Axyz算法的偏差值。

表1 3种定向模型的绝对定向参数及偏差值

由表1可见，PB_Ideal算法中，每放置1次基准尺即解算1次，受基准尺铅垂误差影响较大，造成较大的解算偏差，且算法不稳定、不可靠，最大解算偏差达0.470 mm。而PB_Practical算法依附有限制条件的间接平差模型，将基准尺3次摆放位置的观测数据纳入统一平差系统，绝对定向参数的解算趋于稳定，4组实验中的水平基线长度偏差均未超过0.005 mm，而测站高差偏差均未超过0.05 mm。

3.3 三维坐标解算结果分析

为进一步评判铅垂基准尺综合定向方法的有效性与可靠性，仍以Leica Axyz算法结果为参照，并采用P1～P8共计8个定向点共同参与解算，统计分析PB_Practical测算基准尺端点三维坐标的偏差，如表2所示。可见，本研究所提出的PB_Practical算法，在10 m范围内对三维坐标的测算精度优于±0.03 mm，受限于经纬仪测量系统随测程增大而精度衰减的特性，采用铅垂基准尺综合定向方法所解算的基准尺端点坐标偏差也随测量范围的增大而增大。

表2 铅垂基准尺综合定向方法的三维坐标偏差

实验结果表明，基准尺端点坐标偏差与经纬仪测量系统的测程有关。如图4所示，坐标偏差量随测程的增大而增大，Y、Z坐标方向的偏差稍大于X方向的偏差，但变形量在10 m范围内均未超过±0.03 mm；X坐标的变形不够显著，但不同位置基准尺的端点X坐标的变形方向不同。本研究提出的PB_Practical算法的定向结果在X方向精度优于±0.01 mm，在Y方向精度优于±0.02 mm，在Z方向精度优于±0.03 mm，定向精度与Leica Axyz软件的光束法平差方法相当。

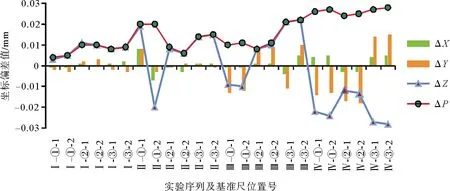
图4 铅垂基准尺综合定向的基准尺端点坐标偏差

4 结束语

本研究给出的基于铅垂基准尺的综合定向方法(PB_Practical)，特别适用于狭小或受限空间下经纬仪测量系统的定向，是对传统“垂直角视距法”的继承与发展。以基准尺严格铅垂的理想模型计算定向参数的初始值，再依附有限制条件的间接平差原理，精确求解综合定向参数。只需交会测量基准尺3个位置，定向结果即可达到Leica Axyz算法的精度水平，具有实用性强、易于编程实现的优势。基于PB_Practical算法，研发了测角三维坐标采集系统3DCoorsA，并应用于玻璃生产线辊子姿态检测、930E大型矿车外形检测等工程，效果良好。

有必要指出的是，为提升经纬仪测量系统的作业效率，基于视觉引导的经纬仪[16-17]、非正交轴系激光经纬仪[19]等新型测量系统已被研制和应用，其定向测量方法涉及图像处理，区别于与传统经纬仪测量系统的定向方法。