裂隙影响基质渗流的数值模拟1)

乔继延 鲁晓兵 张旭辉

(中国科学院力学研究所，北京 100190)

近年来，低渗透油气藏占据我国越来越大的份额，但由于其“低渗透、动用难” 的特点，开采比较困难。低渗透油气藏的孔隙结构复杂，天然微裂缝发育[1-3]，同时孔隙度和渗透率低，因此需要采用人工压裂以增大渗透率[4-7]。

在开发过程中裂隙的存在将显著改变原来基质的渗透流场特性。天然微裂缝之间以平行微裂隙为主，当存在软弱夹层或出现大的构造应力变化时也会出现交叉微裂缝[8]。在生产过程中通常采用水驱，微裂隙的形成为水驱替油提供了阻力更小的流动通道，但又改变了流体压力场的分布，随着微裂隙在几何长度上的增加，水驱过程极易出现水窜等不稳定现象[9]，在这种情况下，注入的水相波及面积减小，直接从微裂隙形成的优势通道流出，大大降低驱油效率。因此，认识裂隙对基质渗流场的影响机理，对于弄清存在裂隙时油气藏的渗流及驱替过程，以及提高采收率具有重要的实际意义。

对于含裂隙的油气藏渗流，人们开展了较多的研究。郑委[10]使用双重逾渗模型展开了孔隙裂隙网络介质连通性和渗透性的研究。刘海娇[11]采用孔隙裂隙网络模型研究了裂隙的长度、密度、方向、位置、间隔以及裂隙长度分形参数对绝对渗透率和驱油效率的影响，发现了由于微裂隙存在导致储层中出现水窜或者死油区的原因。Blunt[12]对非均匀孔隙网络模型进行了研究，并对孔隙网络模型吸入过程中孔穴的充填机制做了详细分析。刘庆杰等[13]运用孔隙网络模型对考虑滑脱效应的致密岩气体渗流进行了模拟研究，并提出了一种适用于孔隙网络模型计算相对渗透率的新方法。刘清泉等[14]基于流量等效的等效渗透系数概念，通过引入贯通系数并结合随机裂隙网络生成技术，发展了一种可用于估算任意二维裂隙等效渗透系数张量的叠加算法。Zheng等[15]和Xiao 等[16]研究了孔隙裂隙双重多孔介质内部渗流系统流动的细节，并模拟了裂缝和基质之间的流体交换。姚军等[17]使用整合法建立了同时考虑大孔隙和微孔隙的双孔隙网络模型，模拟了不同网络结构和润湿性参数对水驱油过程相对渗透率曲线的影响。

前人的这些研究揭示了孔隙和孔隙裂隙油气藏渗流的一些特性，如水驱油过程中的“水窜现象”、滑脱效应、连通性等，但是对裂隙如何改变基质的渗流、如何影响驱替效果等现象研究不深入。一般来说，裂隙渗透性强，渗透阻力小，因此压降也小，于是裂缝间基质的压降也变小，考虑到基质渗透率低，在有些情况下，裂隙间的基质流量将显著减小。一旦发生这种情况，裂隙间基质中的油气流动将大大降低甚至可忽略，驱替时这部分区域将不能被波及到，从而降低采收率。如果弄清了裂隙对基质渗流的这种影响，就可以为人工压裂设计、油气藏开采方案设计提供依据。目前关于这方面的研究还较欠缺。

本文针对孔隙裂隙介质，研究裂隙的空间分布不同以及渗透性不对称条件下，基质中的渗流速度和压力特性，分析裂隙存在对流场的改变。重点分析裂缝之间以及附近流场的变化，进而为孔隙裂隙油气藏开采方案提供参考。

1 稳态渗流模型和数值模拟验证

对于均匀介质的不可压缩流动，连续性方程表述为

式中，u和v为流速。不考虑重力作用，动量方程以Darcy 定律表述为

式中，μ为动力黏性系数，p为压力，kx和ky为渗透率。将速度表达式(2)和式(3)代入连续性方程(1)，得到稳态渗流的控制方程

以有限元数值模拟方法求解上述控制方程。为验证计算的正确性，计算一个简单的稳态渗流问题，几何模型及边界条件如图1 所示(文中除注明外，所有数据均采用国际单位制)。

图1 数值模拟验证的计算简图

渗流介质为水，不计重力和可压缩性。动力黏性系数μ= 10-3，渗透率kx=ky= 19 mD (1 μm2= 1013.25 mD)。很显然，该问题解的解析表达式为p=106(1-x)。根据Darcy 定律，并代入kx，ky和μ的数值，可知在全区域内u=18.753 μm/s，v=0。而数值模拟的结果，u的最大值为18.758 μm/s，最小值为18.746 μm/s。从数值模拟的结果看，计算的相对误差小于0.05%，是可以接受的误差。

2 裂隙在基质中产生的源和汇效应

用数值模拟方法，计算均匀基质中存在双裂隙时的压力和流速分布。计算双裂隙分布于四种不同的位置，计算区域取为1.0×0.5，裂隙长度取为0.20，平行双裂隙间距为0.10，并保持裂隙本身的宽度0.002不变。左端(x= 0) 边界压力p= 1.0 MPa，右端(x= 1.0) 边界压力p= 0 MPa。为便于分析压力和流速分布的特点，截取不同特征位置的水平方向和垂直方向截线，计算简图和截线位置如图2 所示(1a，2a，3a 和4a 在各图中是对称线)。

图2 双裂隙计算简图和截线位置

图3 给出了双裂隙分布于不同位置的条件下，各裂隙入口端和出口端附近区域的速度分布，首先考察平行双裂隙位于中部的情况(图3(a))。在两条裂隙渗透率相同和几何分布对称的情况下，图3(a)给出位于上方裂隙的入口端和出口端附近的流速矢量图。在远离裂隙的地方，流速均匀分布；在入口端，周围基质中的流体向裂隙汇聚(汇)；在出口端，裂隙中的流体向基质扩散(源)。这是因为裂隙的阻力小于基质，因而压降较慢。在裂隙入口端，基质中的压力大于缝内压力，导致基质中的流体流向缝内；而在裂隙出口端，在流经同样距离后，基质中的压力将小于缝内的压力，于是流体从缝内流向缝外。

图3 裂隙端口附近区域的速度分布

在双裂隙垂直交叉分布情况下(图3(b))，在水平裂隙入口端附近，基质中流体流入裂隙，裂隙内部速度逐渐达到稳定的最大值；在两条裂隙的交叉处，垂直裂隙的流体向交叉位置汇聚，经过交叉位置后水平裂隙内流速略有增大。

3 流速和压力分布特征的分析

本节分析在均匀基质中，由于双裂隙的存在，对原流场压力和流速带来变化的机理，并考虑到双裂隙渗透率相同和不相同的情况。在各组计算中，基质的渗透率均取为kx0=ky0=19 mD。双裂隙渗透率相同时，裂隙渗透率均取为kxc=kyc= 1000 mD；裂隙渗透率不同时，渗透率较大者取为kxc=kyc=1000 mD，较小者取为kxc=kyc=200 mD。

3.1 双裂隙渗透率相同的情况

以平行双裂隙位于计算区域中部和垂直交叉双裂隙终于右端(即低压端) 这两种情况为例，进行重点分析。

先看平行双裂隙位于计算区域中部的情况。

在水平流速沿水平方向的分布(图4) 中，离开裂隙一定距离处，水平速度均匀分布。在两条裂隙之间的区域，在入口端和出口端处均存在一个过渡区，速度随距离而变化。裂隙附近的区域，在入口端外，速度快速增加，然后在入口处突降到最小值，进入裂隙后又逐渐增加。在接近出口端时，速度逐渐降低，然后在出口端突增，然后随着离开裂隙的距离而逐渐降低到与基质中的流速相同。两条裂隙正中间的水平线上的水平速度在裂隙入口端外有小幅上升，然后快速下降至一个常数值，在接近出口端，速度又快速上升并略超过基质中的流速，随着离开裂隙而逐渐降低到基质中的流速。正中的流速变化幅度和绝对值均小于裂隙附近。

图4 截线2a ～2d 的水平速度

在远离裂隙的基质区域，裂隙所在的水平段内，水平速度从入口端外逐渐降低，然后逐渐增加；对应于裂隙入口端位置的速度大于裂隙内及附近的速度。这说明裂隙的存在，导致裂隙内外附近局部区域的流速降低，大部分截面流量是由裂隙所贡献的。

在油气开采时，如果存在大量的这种平行对称裂隙，则裂隙附近基质中的流体只能缓慢流出，从而限制产量。对于驱替情形，则大部分驱替流体将通过裂隙流出，裂隙附近的基质中的流体由于压差小，存在不能被驱替的可能。

从裂隙入口端和出口端的水平速度(图5(a) 和图5(b))明显地看出，裂隙内水平速度较基质中的大几个数量级。从垂直速度分布看，在裂隙入口端，流量从基质向裂隙内汇聚(图5(c))，水平速度连续地从小逐渐增加到裂隙内的速度值；在裂隙出口端，则刚好相反(图5(d))。同时，垂向速度绝对值比水平速度小一个数量级。

压力的分布(图5(e) 和图5(f)) 表明，在裂隙的入口(截线2e) 和出口(截线2f) 压力发生突变。在入口端，裂隙渗透率大，压力快速下降，所以周围基质中压力大于裂隙中的压力，于是基质中流体流向裂隙；在出口端，由于裂隙中阻力小，压力降低慢，导致裂隙中压力大于基质中的压力。

图5 截线2e 和2f 的速度和压力分布

再看垂直交叉双裂隙终于右端的情况。根据各条截线上的水平流速分布，在两条裂隙的交叉点上，由于水平和垂直裂隙内流动的相互作用，穿过水平裂隙(截线4a)的水平速度陡然下降(图6(a))，之后在水平裂隙内速度略有增加，这是由于垂直裂隙内流体汇入的结果；在图6(b)中，截线4b 靠近水平裂隙，线上的流速在裂隙入口和出口处发生突变，在入口处上快速增加，紧接着陡然降低， 然后逐渐增加，直到出口处，然后又降低；截线4c 距离水平裂隙较远，与垂直裂隙顶端相交，该线上水平速度在接近水平裂隙入口的位置处逐渐减低， 在垂直裂隙上端口处突然猛然增加，这是由周围基质流体流向垂直裂隙引起的；截线4d 距离两条裂隙都较远，所以流速的变化比较平缓，在靠近水平裂隙入口时，速度开始逐渐降低，直到有边界。而且发现，垂直裂隙内汇入的流体并不多，因此对水平裂隙的影响不是很明显，这是由于在裂隙出入口附近的渗透率发生了突变的缘故。

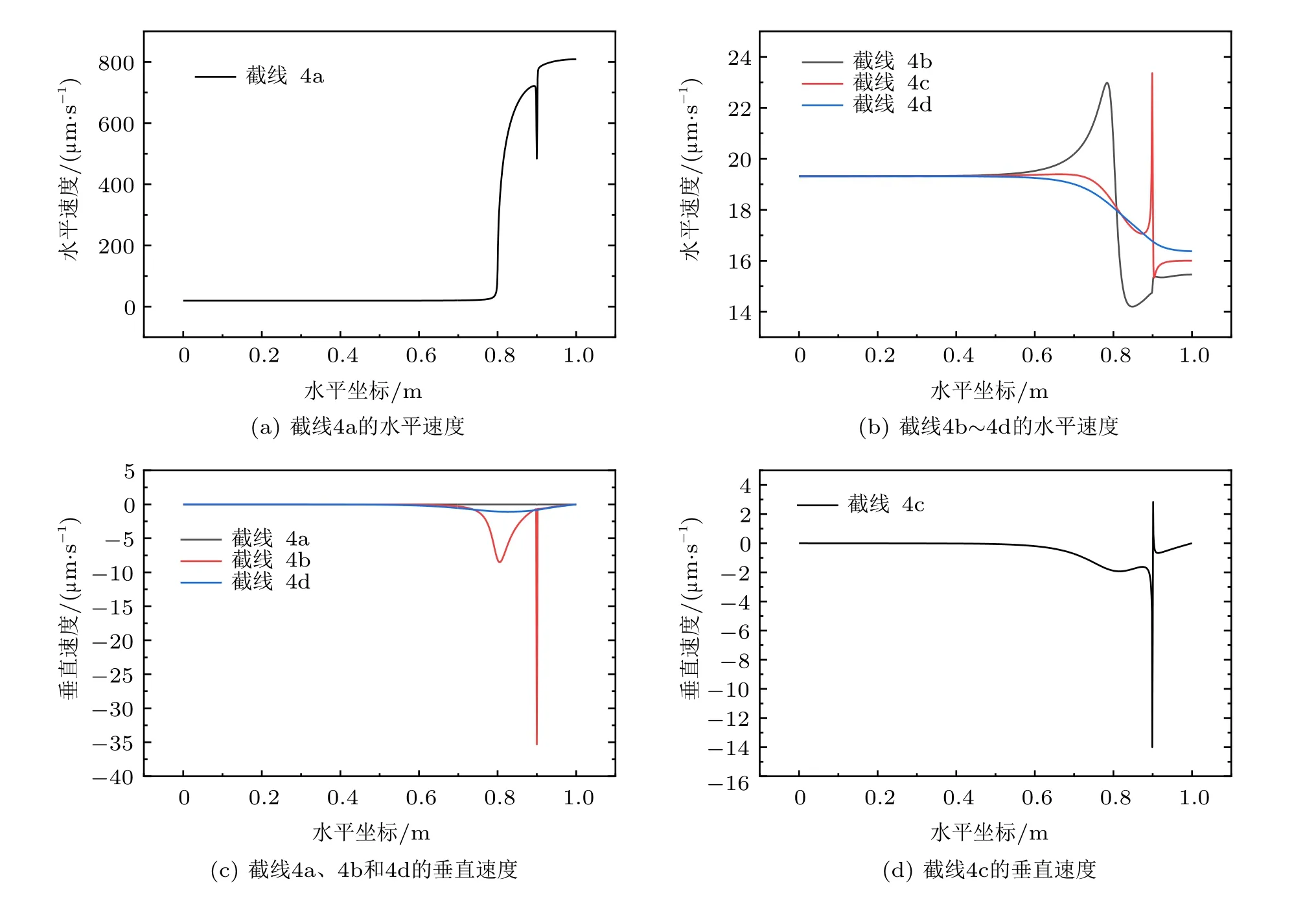
图6 截线4a ～4d 的速度分布

垂向速度沿水平线的分布见图6(c) 和图6(d)。由于裂隙的对称性，截线4a 上的垂直速度为零；截线4b 上只有在垂直裂隙处垂直速度发生突然大幅降低(即向下流动)，在其他地方则基本为零，这是由于基质中的流体快速向裂隙流入的缘故；而截线4d离两条裂隙较远，只在裂隙区域内发生较小的变化。

在经过水平裂隙入口的垂直线上，压力的分布也可以解释速度的特点。如图7 所示，在截线4e 上，水平裂隙入口处的压力梯度最大，在入口上方和下方的压力梯度方向相反，并且都指向裂隙内部；在截线4f 上，垂直裂隙的上下两端和裂隙交叉处，都出现压力梯度的极值和方向的变化(图7(b))。

图7 截线4e 和4f 的速度和压力分布

3.2 双裂隙渗透率不同的情况

两条裂隙渗透率相同时，由于对称性，以缝间中心线为界，靠近入口的上部分基质中流体流向上方裂隙，下方的则相反；中心线上的垂向流速为零。但是当裂隙渗透率不同时，流场压力和流速的这种对称性不再存在。

例如平行双裂隙位于基质中部的情况，当设定上方(y= 0.30) 的裂隙渗透率大于下方(y= 0.20)裂隙渗透率时，发生从小渗透率裂隙向大渗透率裂隙的流动(图8(a))。此时，虽然流体在裂隙之间的区域水平向流量减小，但是一部分将进入裂隙而流走，实际上增加了裂隙之间区域的实际流量。如果是驱替，则可导致驱动面积增加。

再例如平行双裂隙始于高压力边界(左端)的情况，设定上方(y= 0.30) 的裂隙渗透率大于下方(y=0.20)裂隙渗透率。根据图8(b)可知，部分流体将由上方裂隙流向下方裂隙；水平流速与相同渗透率时的情况相比，最大流速也增加了(图8(c))。这就是说，不对称分布的裂隙有利于基质中的流体流向裂隙，裂隙间基质中的水平流动也加强了，因此有利于裂隙间的油气采出。

图8 裂隙渗透率不同时渗流速度的对比

渗透率不等时，裂隙内的最大垂向速度明显增加，渗透率大的裂隙内水平流速增加(图9(a) 和图9(b))。这是因为渗透率越大，压降越快，吸引周围的流体流入的速度也加快。如果裂隙在左侧高压力边界，则裂隙内压力接近左侧边界压力，渗透率大的裂隙内压力大于渗透率小的裂隙内压力，流体从渗透率大的裂隙流向渗透率小的裂隙(图9(c))。

图9 裂隙渗透率不同时渗流速度、压力的分布

4 结论

由于裂隙的渗透率远高于基质，因此在裂隙端部压力发生突变，相应地渗流速度也发生急剧变化；对于基质而言，裂隙入口端等同于汇，开口端等同于源。在油气开采时，如果存在大量平行对称裂隙，则裂隙附近基质中的流体只能缓慢流出，从而限制产量。对于驱替情形，则大部分驱替流体将通过裂隙流出，裂隙附近的基质中的流体由于压差小，存在不能被驱替的可能。而不对称分布的裂隙有利于基质中的流体流向裂隙，裂隙间基质中的水平流动也加强了，因此有利于裂隙间的油气采出。