从空间到时间1)
—— 张量的协变微分学及协变性思想的拓展
殷雅俊
(清华大学航天航空学院工程力学系,北京 100084)
标题显示出了三个关键词:空间域上的协变微分学,时间域上的协变微分学,协变性思想。其中,空间域上的协变微分学成熟于里奇学派。其核心思想,亦即协变性思想,是里奇学派的伟大创见。三个关键词中,只有时间域上的协变微分学是个新词汇。
读者也许会问:“时间域上的协变微分学,与空间域上的协变微分学,有何区别和联系?”本文尝试给出回答。
本文包括如下内容:(1)类比张量的空间协变微分概念,引入张量的时间协变微分概念;(2) 类比张量的空间广义协变微分概念,引入张量的时间广义协变微分概念;(3)类比空间域上张量的协变微分学和广义协变微分学,展示时间域上张量的协变微分学和广义协变微分学;(4)揭示空间域上与时间域上张量的协变微分学之间的对称性,以及广义协变微分学之间的对称性。
1 从历史的天空看张量微分学中的协变性思想
文献[1-4] 曾指出,张量的微分概念不具有协变性。确切地说,张量分量的微分,不再是张量分量。里奇学派敏锐地意识到了张量的微分概念的局限性,他们拓展了协变性思想,定义了张量的协变微分概念。
历史地看,协变微分是里程碑性的新概念––它是协变微分学诞生的标志,不仅为新学科奠定了基础,而且为其发展开辟了新道路。
协变微分学的“运气”可谓好得出奇:一经问世,就大放异彩–– 携手黎曼几何学,为广义相对论奠定了数学基础。广义相对论著名的公设之一,是协变不变性公设。可见,在爱因斯坦心目中,协变性思想居于多么崇高的地位。不仅如此,广义相对论场方程的关键项之一,就是里奇张量的协变导数。显然,没有协变微分学,就没有广义相对论。
历史给予我们启示:协变性思想的任何拓展,都可能具有恒久价值。幸运地是,这样的拓展之路,竟然确凿无疑地存在。拓展之路的起点,仍然是修复对称性破缺的概念以及理论。确切地说,是修复空间与时间之间的对称性破缺–– 空间域上,协变性思想无处不在;时间域上,协变性思想无影无踪。具体地讲,协变性思想起源于空间域,并在空间域上大放异彩。但在时间域上,似乎难觅其踪迹。强烈的反差引起了笔者的注意,由此开启了弥补对称性破缺的进程。现就其中的探索和感悟与读者分享。
2 张量分析学中的对称性破缺
文献[1-2] 已经证实:张量的空间微分与张量的时间微分是对称的概念。基于前者,可发展空间域上张量的微分学;基于后者,可发展时间域上张量的微分学。而空间域上张量的微分学与时间域上张量的微分学,是完全对称的理论。
然而,优美的对称性没能得到延续:
(1) 我们有“张量的空间协变微分” 概念,但没有“张量的时间协变微分” 概念。显然,概念上存在对称性破缺。
(2)我们有空间域上张量的协变微分学,但没有时间域上张量的协变微分学。显然,理论上存在对称性破缺。
我们借助关联图将上述对称性和对称性破缺进行罗列,如图1 所示。

图1 对称性和对称性破缺
为便于读者理解,再就关联图做更细致的类比和解说。
先做纵向类比:历史上,先驱们将张量的空间微分扩展成了空间协变微分,将空间域上张量的微分学发展成了张量的协变微分学。可以追问:与张量的时间微分形影相随,能否扩展出张量的时间协变微分?与时间域上张量的微分学相生相伴,能否发展出时间域上张量的协变微分学?
再做横向类比:与张量的空间微分对应,对称地存在张量的时间微分;与空间域上张量的微分学对应,对称地存在着时间域上张量的微分学。可以追问:与张量的协变微分对应,是否对称地存在张量的时间协变微分?与空间域上张量的协变微分学对应,是否对称地存在时间域上张量的协变微分学?
科学史上有这样的范例:伟大先驱们一旦捕捉到对称性破缺现象,便紧追不舍,匠心独具地弥补破缺,孜孜以求地修复对称。而新的对称性,最终都毫无例外地助产了新的理论。现在,我们在张量分析学中发现了更多的对称性破缺。问题是,能否弥补破缺的对称性?能否构建新的对称性?能否引出新的理论?答案是肯定的。
伟大先哲告诫后人:“历史时常有惊人的相似之处,但决不会简单地重复”。“惊人的相似之处”,意味着我们总能从历史中获得借鉴。“决不会简单地重复”,意味着我们必须有所创造。
3 修复对称性破缺的切入点—— 对称性基因及其遗传
拉格朗日描述下,文献[1-2] 已经成对列出了对称性概念–– 场函数(·) 对拉格朗日坐标xm的微分d(·)(即空间微分) 和对时间t的微分dt(·) (即时间微分)

其中,∂(·)/∂xm是场函数(·)对拉格朗日坐标xm的偏导数(即空间导数),dt(·)/dt是场函数(·) 对时间t的偏导数(亦即物质导数或时间导数)。两个定义式在表观形式上是对称的,在解析结构上也是对称的。由于两个概念非常基本,因此,它们就像两颗对称的种子,内含对称的基因。令对称基因持续不断地遗传下去,便可弥补破缺的对称性。
拉格朗日坐标线嵌入在物体内且随之一起变形,构成随体(或拖带) 坐标系。沿坐标线,基矢量可借助矢径r=r(xm,t) 定义为gm=∂r/∂xm。为方便起见,随体的gm被称为拉格朗日基矢量。空间域上,拉格朗日基矢量的空间导数由克里斯托菲尔公式给出[5]
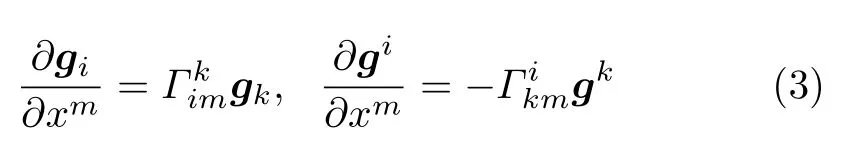
联立式(1) 和式(3),可写出基矢量的空间微分

其中,∇ivk是速度分量vk对坐标xi的协变导数。式(3) 与式(5),式(4) 与式(6),在表观形式上是对称的,在解析结构上也是对称的。
以上述对称性为基础,空间域和时间域上对称化的协变微分学,就可以拉开序幕了。下面,我们以二阶张量为例,展开对称化进程。
拉格朗日描述下,二阶张量场函数T的分解式为

为简单起见,式(7) 中只列出了张量的混变分量。
4 空间域上的协变微分学
空间域上的协变微分学[5-7]是里奇学派的杰作。历史地看,空间协变导数和空间协变微分,是空间域上协变微分学的标志性概念。笔者注意到,先驱们在引出空间协变导数概念时,选择了非常平易的出发点–– 张量对坐标的空间偏导数。式(7) 对坐标xm求偏导数。借助于式(3),可以导出




组合系数是dxm。
至此,空间域上协变微分学的逻辑基础成型了。随后,我们看到了空间域上美轮美奂的建筑–– 奠定在协变微分概念基础之上的协变微分学。
5 时间域上的协变微分学
空间域上,从张量的经典微分学到协变微分学,先驱们精彩纷呈的探索之路,深深地吸引了笔者;先驱们深邃的协变性思想,深深地启发了笔者。2014年,笔者逐渐意识到,协变性思想的探索,应该有两条平行的道路:先驱们走过的协变性之路,是空间域上的协变性道路。与之相对称,还存在着一条平行之路,即时间域上的协变性道路[7-9]。沿着这条对称之路,可以从时间域上张量的微分学,走向时间域上张量的协变微分学。

式(14) 与式(9) 之间的对称性,式(15) 与式(10) 之间的对称性,清晰可见。优雅的对称性,被完整地遗传了下来。

当然,“时空的协变性”,仅仅是作者的个人感知,其真理性远未得到检验。尽管如此,作者确信,协变性是时空的本征性质。或者说,协变性是大自然的本征性质。

进一步可研究张量场函数的时间协变

式(16) 与式(11) 之间的对称性,式(17) 与式(12) 之间的对称性,清晰可见。对称性的遗传,稳定且精准。
正如时间微分与时间导数成正比(式(2)),时间协变微分与时间协变导数也成正比

至此,时间域上协变微分学的逻辑基础齐备了。我们看到了时间域上富丽堂皇的建筑––奠定在时间协变微分概念基础之上的协变微分学。
同时,理论的对称性破缺得以弥补–– 时间域上的协变微分学大厦,与空间域上的协变微分学大厦,构成了对称的建筑群,如图2 所示。

图2
6 从空间协变微分到空间广义协变微分


然而,二者的对称性没有遗传下去。协变性思想确保了∇mui有定义,但∇mui的定义诱发了对称性破缺
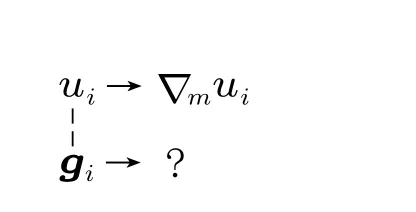
也就是说,空间域上的协变微分学内部,存在对称性破缺现象。这不是个别现象,类似的对称性破缺现象在空间域内普遍存在。要弥补破缺的对称性,必须以合适的方式定义∇mgi,以便建立起∇mui~∇mgi对称
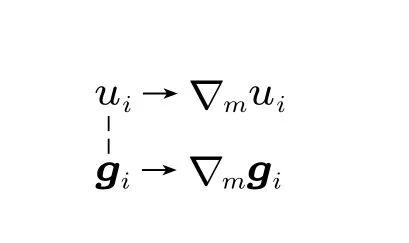
要定义∇mgi,仅有协变性观念是不够的,必须发展广义协变性观念[2,10-13]。
广义协变性是一个新观念。发展新观念,需突破老观念。突破形式有两类,第一类是内部突破,第二类是外部突破。


不同于内部突破,外部突破意味着,从老观念出发引不出新观念,即必须从外部引入新的逻辑基础。更一般地说:问题是在A 学科中提出来的,而解决问题的方案却在A 学科之外(或B 学科之内)。例如,“怎样定义基矢量的空间协变导数∇mgi?怎样定义并基的空间协变导数∇m(gigj)?” 这类问题,是从空间域上的张量协变微分学内部提出来的,但答案却不在其内部而在其外部。
笔者的解决方案,是以新概念为导引,以公理为基础,将广义协变性观念[10-13],从外部赋予空间域上张量的协变微分学。其具体内涵如下。
(1) 抽象出了一个更具一般性的新概念–– 广义分量:
拉格朗日空间域上,满足里奇变换的量,被称为拉格朗日广义分量。

(2) 提炼出了一条极具基础性的公设–– 空间域上的协变形式不变性公设。
拉格朗日空间域上,公设表述如下:
拉格朗日广义分量的空间广义协变导数(或空间广义协变微分),与拉格朗日分量的空间协变导数(或空间协变微分),在表观形式上具有完全的一致性。
表观形式的一致性,就是对称性。因此可以说,协变形式不变性公设,就是对称性公设。公设规定了∇mgi与∇mui表观形式的一致性。这样,就补齐了∇mui~∇mgi对称性。



随着空间广义协变导数(微分) 概念的定义,新的概念对称性破缺出现了,如图3 所示。

图3
下一节我们将弥补概念上的对称性破缺。
7 从时间协变微分到时间广义协变微分

可见,时间域上的协变微分学内部,也存在对称性破缺现象。这也不是个别现象,类似的对称性破缺现象在时间域上普遍存在。要补全破缺的对称性,也必须发展时间域上的广义协变性观念。
时间域上的广义协变性观念[2,8-9,14],不可能从时间域上的协变微分学内部产生,需借助于公理化思想从外部引入。于是有拉格朗日时间域上的协变形式不变性公设:
拉格朗日广义分量的时间广义协变导数(或时间广义协变微分),与拉格朗日分量的时间协变导数(或时间协变微分),在表观形式上具有完全的一致性。

注意到,式(21)、式(22) 与式(19)、式(20) 完全对称。这样,概念上的对称性破缺被补齐了,如图4 所示。
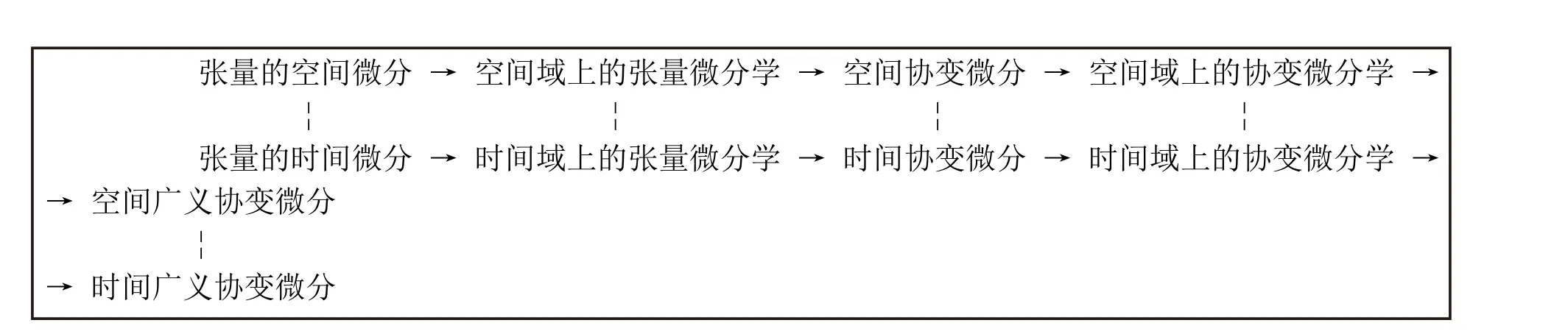
图4
8 空间域上的广义协变微分学
“概念+公设”,就构成了公理化系统的基本要素。拉格朗日空间域上的公理化系统,就是拉格朗日空间域上的广义协变微分学[2,10-13]。

这个线性变换,可以推广到任意广义分量。
张量T是特殊的广义分量。其空间广义协变导数∇mT和空间广义协变微分DT,可以按照公设定义,并可以证实有
这是赏心悦目的结果。式(24)结合式(9)和式(11),可知

至此,空间域上广义协变微分学的轮廓,清晰化了。
然而,理论上新的对称性破缺又出现了,如图5所示。

图5
下一节我们将弥补理论上的对称性破缺。
9 时间域上的广义协变微分学
弥补理论上新的对称性破缺并不困难:既然公理化思想能将空间域上的协变微分学拓展为广义协变微分学,那么,公理化思想也能将时间域上的协变微分学拓展为广义协变微分学[8-9,14]。
这个比例变换,可以推广到任意广义分量。
对于张量T,其时间广义协变导数∇tT和时间广义协变微分DtT,可按照公设定义,且可以证实有
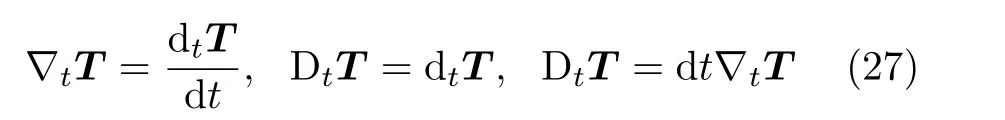
式(27) 结合式(14) 和式(16),可知
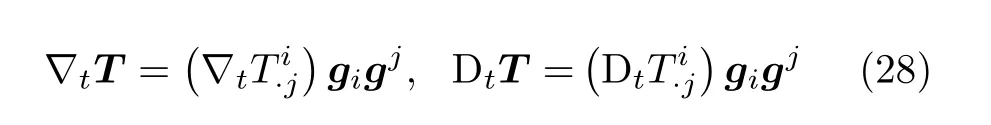

至此,时间域上广义协变微分学的轮廓,清晰化了。
注意到,式(26)~式(28)与式(23)~式(25)完全对称。可以说,时间域上的广义协变微分学,与空间域上的广义协变微分学,完全对称。形象地讲,时间域上广义协变微分学的大厦,与空间域上广义协变微分学的大厦,构成了完美对称的建筑群,如图6所示。

图6
再从整体上鸟瞰一下:从左到右,我们看到了平行对称的三组建筑群:第一组是空间域上的张量微分学与时间域上的张量微分学;第二组是空间域上的协变微分学与时间域上的协变微分学;第三组是空间域上的广义协变微分学与时间域上的广义协变微分学。本文按顺序依次描绘了三组对称建筑群的构建历程,井然有序,一气呵成,顺畅自然。然而,笔者必须坦诚地告诉读者:真实的探索过程远非如此轻松愉快。恰恰相反,一路磕磕绊绊,曲折反复,多次功败垂成。读者也许会质疑:本文中的构建进程完全异于真实的探索过程,是否有“篡改历史”的嫌疑?
笔者联想到学生时代的经历。当年学习麦克斯韦方程组,深为其优美、庄严、深刻所折服。然而,查阅历史后才发现,教科书中的描述,与麦克斯韦真实的探索过程,完全不是一回事。教科书中的麦克斯韦方程组,是千锤百炼后的完美形态,与其诞生时的初始形态相比,自然有面目全非之感。然而,我们并不能指责教科书伪造了历史。
笔者引用高斯的名言做注脚:“漂亮的大厦建成了,谁还会留下脚手架?”
10 空间域上广义协变微分学的可计算性
空间域上,要使广义协变微分学具有可计算性,必须澄清基矢量的空间广义协变导数和空间广义协变微分[2,10-13]。本节同时关注一个问题:透过广义协变性思想的透镜看空间,能看到什么?
拉格朗日基矢量gi的空间广义协变导数∇mgi,可根据公设,仿照矢量分量ui的空间协变导数∇mui,定义成
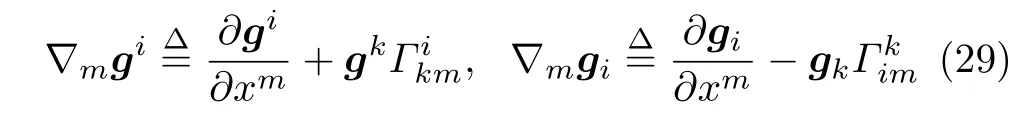
仿照矢量分量ui的空间协变微分Dui,拉格朗日基矢量的空间广义协变微分可定义为
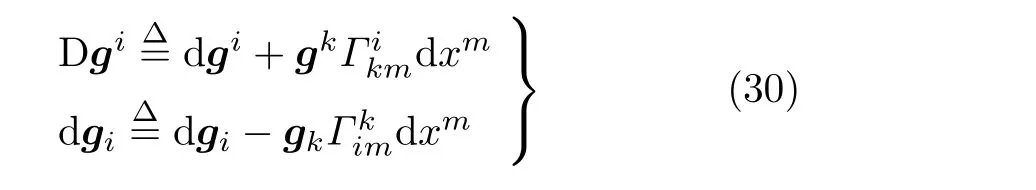
基于上述定义,可以从空间广义协变性的角度,研究空间的性质。立即发现,基矢量的空间广义协变导数和空间广义协变微分均恒为0,即
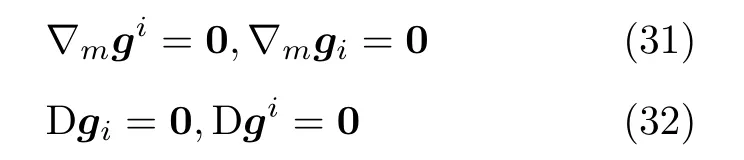
一旦基矢量的空间广义协变导数(微分) 可计算,空间域上的广义协变微分学,就具有了可计算性。
前期的研究中,式(31) 和式(32) 被称为“空间域上的协变微分变换群”。这一变换群下的不变性质,就构成了空间域上广义协变微分学的核心内容。
基矢量的空间广义协变导数(微分) 恒为0,其物理意义,已经在前期的综述论文中得到阐释:融入基矢量的观察者(简称“随基观察者”) 看到的基矢量的空间变化率,就是基矢量的空间广义协变导数。由于观察者随着基矢量的伸长而伸长,随着基矢量的转动而转动,因此,他根本感受不到基矢量的空间变化率,或者说,他感受到基矢量的空间变化率恒为零。
这里引用前辈力学家武际可先生的观点:“基矢量的协变导数恒为零,是随基观察者牵连运动的必然结果。” 笔者将武先生的观点称为“运动的观点”–– 观察者站在基矢量上,随之一起运动,这是牵连运动。由于随基观察者完全融入了基矢量,因此,他看到的相对运动,就恒为零。笔者认为,这是非常漂亮的思想,完美地把数学与力学融成了一体。这是影响广泛的命题。可以推知,由基矢量的乘法运算生成的任何广义分量,其空间广义协变导数和空间广义协变微分均恒为零。下面是满足命题的例子。
度量张量分量的空间广义协变导数和空间广义协变微分均恒为0
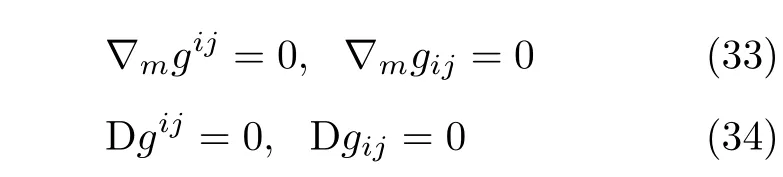
度量张量是空间长度度量的“刻度”。其空间广义协变导数(微分) 为零,正是随基观察者看到的结果。

度量张量的杂交分量[2,15]的空间广义协变导数和空间广义协变微分均恒为0度量张量杂交分量就是坐标变换系数。它不仅是空间长度度量的“刻度”,而且是坐标变换的“担当者”。其空间广义协变导数(微分) 恒为0,正是随基观察者看到的图像。

我们该如何理解空间域上的“0” 结果?作者认为,“0”结果表明,空间具有协变性。可以大胆推断:协变性是空间的本征性质。
没有空间域上的广义协变微分学,我们感知不到空间的协变性。这涉及到一个“诡异” 的问题:空间的协变性,是客观实在,还是人为的塑造?笔者倾向于认为,尽管空间广义协变微分是人造的概念,但由其刻画的空间协变性,是客观的,是不以人的意志为转移的。
特别要指出的是,大量的“0”结果,使得空间域上的广义协变微分学,变得致精致简。
11 时间域上广义协变微分学的可计算性
时间域上,要使广义协变微分学具有可计算性,必须澄清基矢量的时间广义协变导数和时间广义协变微分[7-9]。本节同时关注一个问题:透过广义协变性思想的透镜看时间,能看到什么?
按照公设,拉格朗日基矢量的时间广义协变导数∇tgi,仿照矢量分量ui的时间协变导数∇tui,可定义成
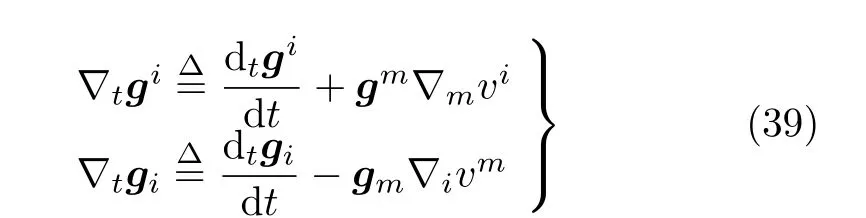
依据公设,仿照矢量分量ui的时间协变微分Dtui,拉格朗日基矢量的时间广义协变微分可定义为

注意到,式(39)、式(40) 与式(29)、式(30) 完全对称。在这样的定义下,就可以从时间广义协变导数(微分)的角度,研究时间的性质。立即发现,基矢量的时间广义协变导数(微分) 恒为0,即
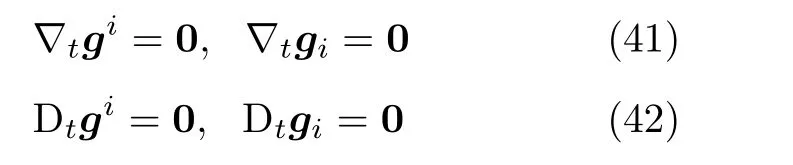
一旦基矢量的时间广义协变导数(微分) 可计算,拉格朗日时间域上的广义协变微分学,就具有了可计算性。式(41)和式(42)被称为时间域上的协变微分变换群。这一变换群下的不变性质,就构成时间域上广义协变微分学的核心内容。
基矢量的时间广义协变导数(微分) 恒为0,其物理意义,可以这样阐释:随基观察者看到的基矢量的时间变化率,就是基矢量的时间广义协变导数(微分)。他随着基矢量的伸长而伸长,随着基矢量的转动而转动,因此,他根本感受不到基矢量的时间变化率,或者说,他感受到了0值。
请读者再次回顾一下武际可先生运动的观点。注意到,式(41)、式(42) 与式(31)、式(32) 完全对称。
如下命题自然成立:基矢量的乘法运算给出的任何广义分量,其时间广义协变导数(微分) 均恒为0。满足命题的案例如下。度量张量分量的时间广义协变导数(微分) 恒为0,即

随基观察者感觉不到度量张量的时间变化率。注意到,式(43)、式(44) 与式(33)、式(34) 完全对称。
作为坐标变换系数,度量张量的杂交分量的时间广义协变导数(微分)[2,15]恒为0,即

我们该如何理解时间域上的“0”结果?“0”结果意味着,时间具有协变性。大胆推测:协变性是时间的本征性质。
没有时间域上的广义协变微分学,我们感知不到时间的协变性。这涉及到一个“诡异” 的问题:时间的协变性,是客观实在,还是人为的塑造?笔者倾向于认为,尽管时间域上的广义协变微分是人造的概念,但由其刻画的时间协变性,是客观的,是不以人的意志为转移的。
特别要指出的是,大量的“0”结果,使得时间域上的广义协变微分学,变得致精致简。
12 时空的协变性
如上所述,空间具有协变性,时间也具有协变性。联合起来,就可以说,时空具有协变性。或者说,协变性是时空的本征特性。
当我们谈及场函数,一般都是指外加在空间域上的函数,例如,应力张量场函数,应变张量场函数,等。实际上,空间域自身也有场函数,例如,基矢量场函数,度量张量场函数,等。空间域自身的场函数,刻画的是空间自身的本征性质,因此,可称之为空间的本征场函数。
协变性思想,虽然是从外加张量场函数引出来的观念,但也适用空间的本征场函数。时空上的“0”结果,正是协变性思想与空间本征场函数相结合的产物。“0” 结果,是本征场函数的空间协变微分不变性质,也是本征场函数的时间协变微分不变性质。也可以说,“0” 结果,是时空的协变不变性质。没有广义协变性思想的透镜,不可能看见如此抽象的不变性质。
时空,是力学研究永恒的参照“背景”。理解时空的本性,是力学探索者永恒的使命。笔者曾经认为,力学发展到今天,对时空的理解,已臻完美无缺。然而,随着协变性思想的拓展,笔者改变了看法:时空仍然是力学中有待深入理解的对象之一。
力学研究物质的运动,而任何运动都发生在特定的时空,都要受到时空的约束。这样的约束,必然体现在刻画运动的自然规律中:因为时空具有协变性,因此,自然规律必然具有协变性。于是,我们有一般性命题:正是时空的协变不变性,决定了自然规律的协变不变性。
由此看来,广义相对论将“协变不变性”提升到至高无上的公理地位,绝对是无与伦比的高明之举。
透过广义协变性思想的透镜,我们看到了美丽、对称、协变的时空!
13 结论
空间域上的协变微分学是先驱们的经典之作,极大地推动了物理学和力学的发展。笔者期待,时间域上的协变微分学,能够像空间域上的协变微分学一样,成为物理学和力学探索者开疆拓土的利器。
对称性贯穿本文始终。空间域上的协变微分学与时间域上的协变微分学,概念是对称的,概念的解析结构是对称的,理论体系是对称的。当然,空间和时间也是对称的。对称性,大都表现为解析结构的相似性,以及代数结构的一致性。
空间域上的协变微分学与时间域上的协变微分学的对称性,是偶然的巧合吗?笔者的答案是否定的。如此精致的对称性,昭示着某种客观性和必然性。当然,要刻画空间域上的广义协变微分学和时间域上的广义协变微分学,人为塑造的概念必不可少。虽然人为塑造的概念是主观意志的产物,但人造概念揭示出的广义协变性和对称性,却是客观实在。

