不同围压下砂岩渗透性规律试验研究

侯宜峰，吴小刚，唐 恺，周玉新

(1.中钢集团马鞍山矿山研究总院股份有限公司，安徽马鞍山243000；2.金属矿山安全与健康国家重点实验室，安徽马鞍山243000)

矿山建设工程中，地质环境复杂(高应力、高渗透水压力等情况)，不仅会造成突发性工程灾害等问题，而且给矿山开采带来严重挑战。当前工程中岩体的渗透率主要通过现场水文地质试验测定，测定方法主要有压水试验和抽水试验等。然而不同深度的岩石处于不同的应力水平和变形阶段，即裂隙发育情况不同，相应的岩体渗透性也不同，仅通过现场试验获取渗透率并不准确[1]。研究渗流-应力耦合作用下岩石渗透率的变化规律，一定程度上可弥补现场试验缺乏针对性的不足。张守良等[2]试验研究了岩石渗透率与应力状态中相关力学参数之间的关系，建立了渗透率与应力状态之间的关系模型；王环玲等[3]通过岩石渗流-应力耦合试验，分析轴向应变和环向应变对渗透率的影响，结果表明岩石的环向变形比轴向变形更能反映岩石渗透性的演化规律；姜振泉等[4]针对软硬岩石在变形过程中渗透率变化的特点，分析了渗透率产生差异的原因，认为岩石在变形破坏过程中的渗透率主要取决于破坏的形式和特征；Hu等[5]试验研究了饱和砂岩的力学和渗透率，得到Biot系数和渗透率随微裂纹扩展的演化规律。

目前，深部开采是矿山开发的发展趋势，深部围岩所处环境异常复杂，岩体在高应力和高渗透水压力的耦合作用下易产生明显的失稳变形。具有高渗透性的砂岩是地下工程中最常见的地质岩体之一[6]。为此，定量分析渗流-应力耦合作用下砂岩渗透率的演化规律，以期为矿山建设提供一定的基础理论与依据。

1 试验原理及方法

1.1 试验岩样

试验岩样为南京砂岩，颗粒组成分布均匀，外观无明显裂隙。经钻孔取芯、切割、打磨，外观均匀细密两端平整，无可见天然裂纹。根据国际岩石力学学会(ISRM)推荐的标准尺寸，将试验岩样制成直径为50 mm，高为100 mm 的圆柱形。试验岩样如图1。

图1 砂岩试验岩样Fig.1 Sandstone test sample

1.2 试验仪器

试验仪器为岩石全自动三轴伺服试验系统，该系统拥有全自动自平衡三轴压力室，具有轴向位移、环向应变、泵流量等传感器以及数据采集储存系统。

1.3 试验原理

为获得砂岩在不同围压下渗透率随压缩破坏的演化规律，采用稳态法测量砂岩的渗透率，并作假定[7-8]：岩体内部初始孔隙和原生裂纹分布均匀，视为孔隙介质；恒压稳定渗流视为连续渗流；渗透水不可压缩；对于渗透率k≥10-19m2的砂岩试样，通过实测流量计算岩石的渗透率。根据达西定律推导出渗透率k的计算公式为

式中：μ 为水的黏滞系数，取μ=1×10-3Pa·s(水温20 ℃)；V 为Δt 时间通过试样的水流体积，m3；L为试样的高度，m；A 为试样的横截面积，m2；Δp 为试样上下两端的渗透压差，Pa；Δt 为记录的间隔时间，s。

1.4 试验步骤

试验前，对岩样抽真空饱和，抽真空时间大于8 h，使孔隙内充满水，达到饱和状态。具体试验步骤如下：

1)将岩样装入橡胶套内，并用箍环密封，确保试验过程中压力室中的油与岩样中的水不连通；

2) 给压力室充油并设置围压为5，10，15，20 MPa，待围压稳定后施加渗透压差3 MPa；

3)以3.0 MPa/min的加载速率施加轴向荷载直至岩样破坏；

4)试验结束取出岩样(图2)，对试验仪器自动存 储的数据进行处理，得到应力-应变曲线，并计算出设定时间内通过岩样的水体积，再通过式(1)计算出某时刻对应的岩样渗透率。

图2 岩样破坏形式Fig.2 Rock-like destruction

2 试验结果与分析

2.1 渗透率与轴向应变关系

不同围压下岩样的偏应力和渗透率与轴向应变曲线如图3，4。由图3，4可知：随着围压的增大，偏应力与渗透率达到峰值时对应的应变越大，岩样的变形由脆性逐渐向延性转化；砂岩渗透率的变化规律与应力-应变有密切关系，不同围压下砂岩渗透率-轴向应变曲线趋势基本一致；在达到峰值强度前的弹性阶段，砂岩渗透率随轴向应变的增大而降低，这是因为随着轴向应变的增大，原生微裂隙被压密使渗透率略微降低；弹塑性阶段后，随着新裂缝的扩展和贯穿，渗透率先缓慢增加，后急剧增大至峰值，渗透率峰值出现在岩样破坏后的残余强度阶段，即岩样强度峰值后。

图3 偏应力与轴向应变关系曲线Fig.3 Relationcurvesbetween deviatorstress and axialstrain

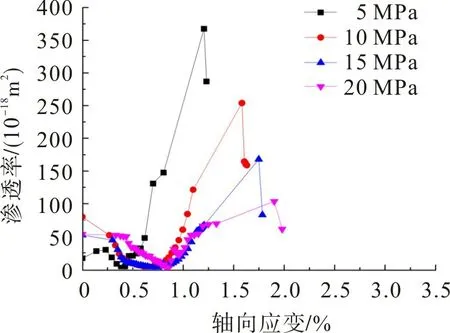
图4 渗透率与轴向应变关系曲线Fig.4 Relation curves between permeability and axial strain

2.2 渗透率与环向应变关系

不同围压下砂岩的偏应力和渗透率与环向应变曲线如图5，6。由图5，6可知：环向应变与渗透率的变化规律类似，弹性阶段，环向应变增长较慢，且增幅较小，对应渗透率略微降低；弹塑性阶段，环向应变增长较快，对应渗透率先略微增大后急剧增大。由图3，5可知，轴向的弹性应变大于环向的弹性应变，环向变形比轴向变形更早地进入弹塑性阶段；弹塑性阶段，环向应变的增长幅度大于轴向应变，先略微上升后急剧上升，与渗透率的发展规律相符，相较而言环向应变比轴向应变更能反映渗透率的发展规律。

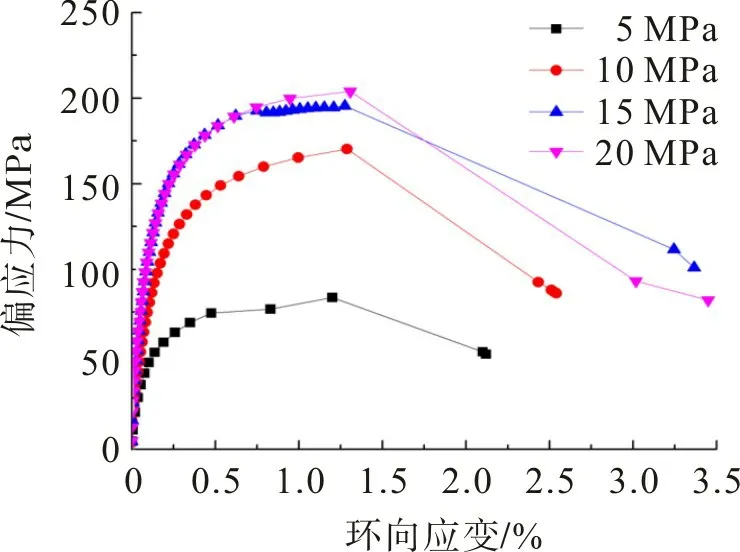
图5 偏应力与环向应变关系曲线Fig.5 Relation curves between deviator stress and annular strain

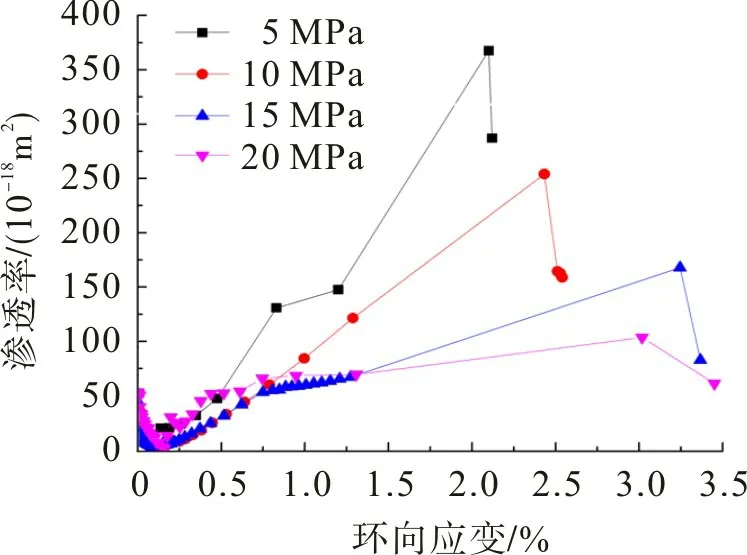
图6 渗透率与环向应变关系曲线Fig.6 Relation curves between permeability and annular strain

由图4，6可知：试验过程中，岩样的轴向应变和环向应变不同阶段的渗透率演化规律基本一致，这是由于弹性阶段岩样原生微裂隙较少，渗流主要发生在岩样孔隙中，随着原生岩石孔隙被压实，渗透率略有下降；弹塑性阶段原生裂缝和新裂缝逐渐连通，渗流开始逐渐通过裂隙发生，渗透率的增长速率逐渐增大；残余强度阶段，岩样发生破坏，并出现贯穿性裂隙，岩样的渗透率急剧上升至峰值，而后由于贯穿性裂隙被围压压密，岩样渗透率开始降低。

2.3 渗透率与体积应变关系

岩样在加载破坏过程中，渗透率与岩体变形关系紧密，体积应变更适用于表达岩石扩容特性与渗透率的演化关系。岩石的体积应变按下式计算

式中：ε1，ε2和ε3分别为岩石的体积应变、轴向应变和环向应变。

不同围压下砂岩的偏应力和渗透率与体积应变关系曲线见图7，8。由图7，8可知，体积应变在变形过程中主要历经压缩和扩容2个阶段。体积压缩阶段，岩样的渗透率随偏应力的增加而降低，在偏应力作用下，岩石的原始孔隙达到最大压实点，岩石渗透率趋于最小值，并非最小值，渗透率最小值出现在体积应变的转折点前[8]；随着偏应力的增加，岩石试样进入扩容阶段，岩石试样的渗透率随偏应力的增加而增加，在屈服阶段达到峰值。

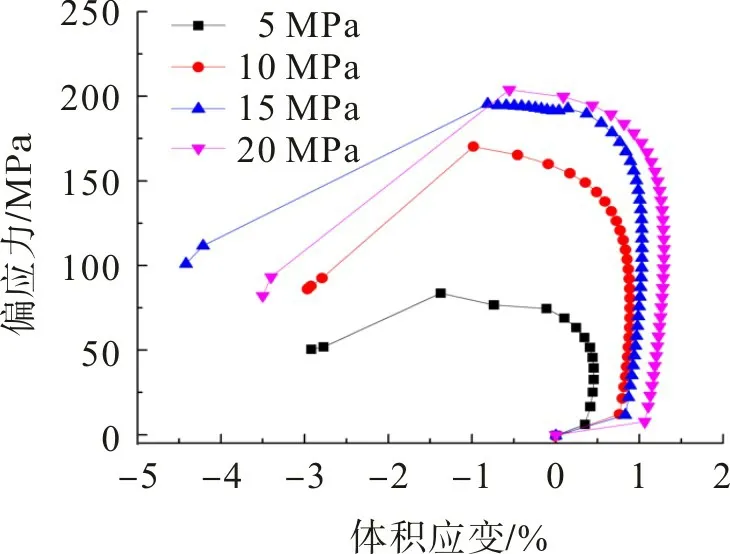
图7 偏应力与体积应变关系曲线Fig.7 Relation curves between deviator stress and volumetric strain

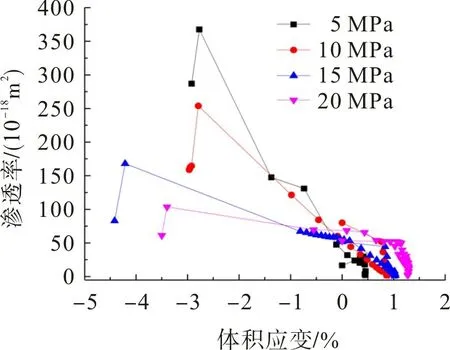
图8 渗透率与体积应变关系曲线Fig.8 Relation curves between permeability and volumetric strain

不同围压下最大压密点与最小渗透率对应的体积应变见表1。由表1 可知：随着围压从5 MPa 增加到20 MPa，岩样的最大压密点对应体积应变分别增长了93.4%，15.7%，25.2%；不同围压作用下，最小渗透率对应的体积应变小于最大压密点，岩样渗透率最小值并非出现在岩样体积的压密最大处，而是出现在最大压密点前；围压为5 MPa时，岩样最小渗透率最大，为围压10，15，20 MPa中最小渗透率最小值的5.5倍。由此可知，围压的增大增加了岩石的延性，阻碍了岩样原生与新生裂隙的扩展，并且影响岩样的最小渗透率。

表1 不同围压下最大压密点与最小渗透率对应的体积应变Tab.1 Volume strain corresponding to the maximum dense point and minimum permeability under different containment pressures

3 结 论

1)偏应力与渗透率达到峰值时对应的应变随着围压的增大而增大，岩样的变形由脆性逐渐向延性转化；轴向应变和环向应变不同阶段的渗透率演化规律基本一致，但环向应变比轴向应变更能反映渗透率的发展规律。

2)砂岩渗透率的变化规律与应力-应变关系密切：弹性阶段，岩样渗透率随应变增大而降低；在弹塑性阶段，渗透率随应变增大先缓慢增加后急剧增大；残余强度阶段，岩样的渗透率急剧上升至峰值，而后开始下降。

3)砂岩的体积应变在变形过程中主要历经压缩和扩容2个阶段：体积压缩阶段，砂岩的渗透率随偏应力的增加而降低；扩容阶段，渗透率随偏应力的增加而增加，在屈服阶段达到峰值。

4)不同围压下，砂岩最小渗透率对应的体积应变小于最大压密点处对应的体积应变，渗透率最小值并非出现在岩样体积的压密最大处，而是出现在最大压密点前，围压的增大阻碍砂岩原生与新生裂隙的扩展，从而影响岩样的最小渗透率。