Colpitts混沌电路的线性反馈控制及自适应反馈控制

张中华，周健博，付景超

(东北电力大学理学院，吉林 吉林 132012)

自洛伦兹提出第一个混沌模型[1]以来，人们对于混沌系统的研究取得了飞速发展，其中混沌系统的研究方向也出现了分支：量子混沌[2-5]、混沌耦合与同步[6-9]、混沌吸引子[10-13]、混沌控制[14-16]等.1983年，蔡少棠教授提出了一种简单的非线性电子电路设计，即著名的蔡氏电路[17].1994年，爱尔兰学者Kennedy教授首次发现了Colpitts电路可以在工作时产生混沌振荡[18]，此后Colpitts混沌电路[19]逐渐被人们关注，并成为一个研究热点.近些年来，已有许多学者对于Colpitts混沌电路的动力学行为进行了深入的研究[20-21].研究表明Colpitts振荡电路在许多领域都有广阔的应用前景，最显著的就是微波频段混沌信号发生器.由于Colpitts混沌电路产生的混沌信号带宽更宽、频率更高，因而更符合超宽带通信与混沌雷达等应用领域的需要[22].同时，对于Colpitts混沌电路的控制方法[23-24]的研究也开始变得引人瞩目.本文通过数值仿真对Colpitts混沌系统[25]的混沌现象的进行了验证，并设计了线性反馈控制器和自适应反馈控制器稳定Colpitts混沌系统，仿真证实了两种反馈控制的有效性.

1 Colpitts振荡电路的动力学分析

典型的Colpitts振荡电路[25]如图1所示.其中，三极管作为电路中唯一的非线性器件，是电路产生混沌振荡的核心.

Colpitts振荡电路无量纲后的数学模型为

(1)

公式中：η(y)=exp(-y)-1是唯一的非线性项.

引理1[25]该混沌电路有且只有一个平衡点S0=(0，0，0)，且该平衡点当k=0.5，Q=1.4158，g=3.162 3时，Colpitts振荡电路会产生混沌振荡.

系统的混沌吸引子如图2所示；系统状态变量随时间变化的时域波形图如图3所示.

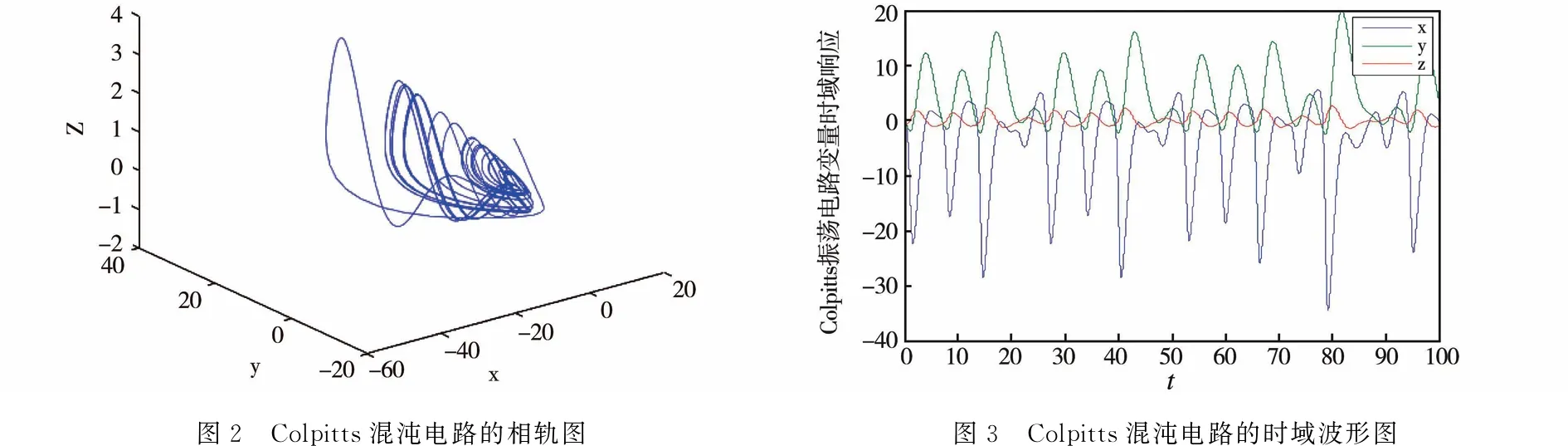
图2 Colpitts混沌电路的相轨图图3 Colpitts混沌电路的时域波形图

(2)

2 Colpitts混沌电路的线性反馈和自适应反馈控制

2.1 线性反馈控制

2.1.1 线性反馈控制器

受控系统(3)如下所示，

(3)

这里U=(u1，u2，u3)T为要设计的控制器.令U=(u1，u2，u3)T=(0，βy1，0)T，其中β是反馈系数.系统(3)变为

(4)

系统(4)在S0(0，0，0)的雅可比矩阵为

特征方程为

Δ(λ)=λ3+A1λ2+A2λ+A3，

A1=d-β，A2=-βd+ac+bc，A3=abc-βac

根据Routh-Hurwitz判据，当

受控系统(3)在平衡点S0(0，0，0)处渐进稳定.

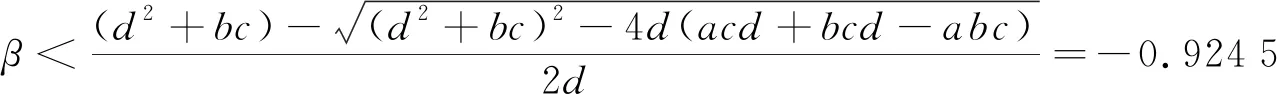
目前，人力资源管理信息化软件产品的规则与质量，在社会市场上的标准还不统一，产品还不规范，销售厂商较为混杂，这些问题都在一定程度上制约着人力资源管理的信息化发展。

2.1.2 数值仿真

k=0.5，Q=1.4158，g=3.1623，取反馈系数β=-1和β=-1.5，受控Colpitts混沌系统的时域波形如图4、图5所示.

图4 β=-1时受控Colpitts混沌系统的时域波形图图5 β=-1.5时受控Colpitts混沌系统的时域波形图

2.2 Colpitts混沌电路的自适应反馈控制

2.2.1 自适应反馈控制器

当k=0.5，Q=1.415 8，g=3.162 3时，受控混沌系统(3)如下

(4)

设控制目标为α1=0，α2=C1e1，α3=C2e1+C3e2，控制误差为e1=x-α1，e2=y-α2，e3=z-α3.将控制误差带入受控系统，可得如下的误差系统

令

u3=cx+(c+dC3)y，

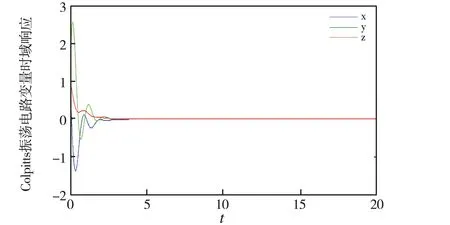
图6 受控Colpitts混沌系统的时域波形图

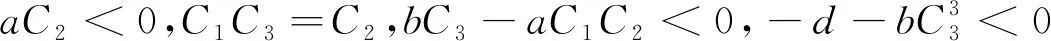
2.2.2 数值仿真

令k=0.5，Q=1.415 8，g=3.162 3，受控Colpitts混沌系统如图6所示，此处C1=0.97，C2=-0.97，C3=-1.

3 结 论

文章研究了Colpitts混沌电路的控制问题.分别设计了线性反馈控制器和自适应反馈控制器，数值仿真验证了两种控制器均可以将混沌系统控制到平衡点，且自适应控制的效果明显好于线性反馈控制的效果.