Scaled Preconditioned Splitting Iterative Methods for Solving a Class of Complex Symmetric Linear Systems
DUAN Yonghong(段永红),WEN Ruiping(温瑞萍),GAO Xiang(高翔)
(1.Department of Mathematics,Taiyuan University,Taiyuan 030600,China;2.Key Laboratory for Engineering & Computing Science,Shanxi Provincial Department of Education,Taiyuan Normal University,Jinzhong 030619,China)
Abstract:This paper constructs two scaled preconditioned splitting iterative methods for solving the system of linear equations when the coefficient matrix is a non-Hermitian but symmetric complex matrix.The formula of the optimal parameters and the spectral radius properties of the iteration matrix for the new methods are discussed in detail.Theoretical analyses show that the new methods are convergent under the reasonable conditions.Finally,the numerical experiments show the new methods to be feasible and effective.
Key words:Complex symmetric matrix;Splitting iterative method;Convergence;Preconditioned
1.Introduction
We consider the iterative solution of the linear systems
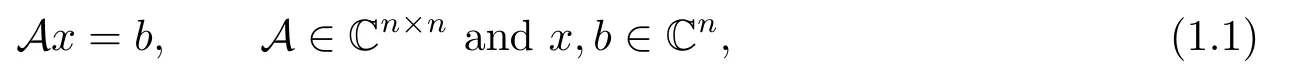
whereA=W+iTis a non-Hermitian but symmetric matrix(=AT)withW,T∈Rn×nare real and symmetric,andWbeing positive definite andTpositive semidefinite.Here and in the sequel,we use i(i2=-1)to denote the imaginary unit.LetA=M-Nbe a splitting of the matrixA∈Cn×n,i.e.,M∈Cn×nis nonsingular andN∈Cn×n.Then a fixed point iterative method induced by this splitting has the form
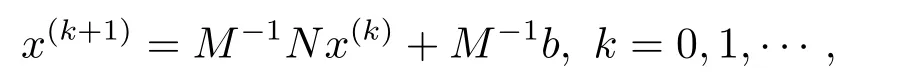
wherex(0)∈Cn×nis a given starting vector.
Such systems(1.1)arise in many important areas in a variety scientific computing and many important engineering applications.We mention just a few:
·diffuse optical tomography[1];
·FFT-based solution of certain time-dependent PDEs[2];
·structural dynamics[3];
·lattice quantum chromodynamics[4];
·molecular scattering[5];
·numerical computations in quantum mechanics[6].
Recently,for solving the systems(1.1)efficiently,Axelsson and Kucherov[7]presented the real valued iterative methods,Benzi and Bertaccini[8]proposed the block preconditioning of real-valued iterative algorithms,BAI et al.[9-11]introduced the modified Hermitian and skew-Hermitian splitting(MHSS)as well as PMHSS iterative methods,ZHAO et al.[12]put forward a single-step MHSS method(SMHSS)and its variants with a flexible-shift(f-SMHSS).WEN et al.[13-14]suggested also some iterative methods and preconditioned iterative methods;Van der Vorst and Melissen[15],Freund[16],Bunse-Gerstner and Stver[17]presented the conjugate gradient-type methods;Clements and Weiland[18]introduced the Krylov-type methods.For details one can refer to[1-19]and the references given therein.
Considering a preconditioned system of(1.1)

wherePis a nonsingular matrix.The corresponding iterative method is given in general by
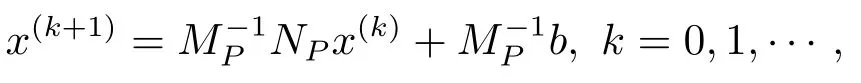
wherePA=MP-NPis a splitting ofPA.
Some techniques of preconditioning which improve the convergent rate of these iterative methods have been developed.For example,ZHENG et al.[19]introduced a double-step scale splitting(DSS)iterative method by using the scaled technique.By multiplying two parameters(α-i)and(1-iα)both sides of the linear systems(1.1),two equivalent systems can be respectively yielded,i.e.,(α-i)Ax=(α-i)band(1-iα)Ax=(1-iα)b,whereαis a real positive number.Then two fixed-point equations can be generated as follows,
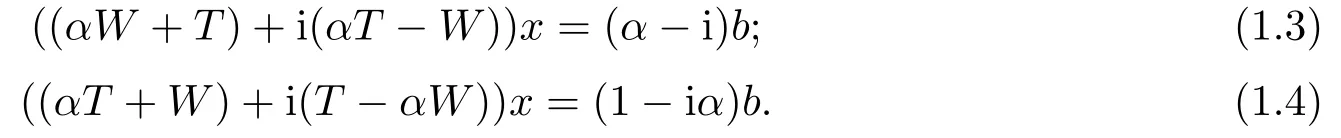
The authors of[19]extended the idea of the PMHSS iterative method[11],and suggested the following iterative scheme alternatively:
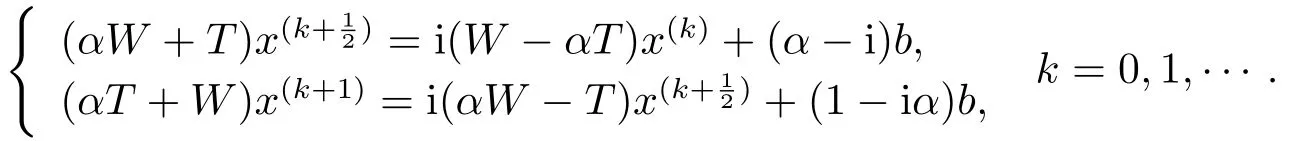
Whereas the systems(1.3)and(1.4)are in fact two preconditioned systems(1.2)whenP=(α-i)IandP=(1-iα)I,that is to say,the preconditioned matrices are both the scalar matrices.The(1.3)and(1.4)are the same whenα=1.Therefore,the alternation of the DSS iterative method was only carried out in twins of two preconditioned systems.
In order to solve a class of the system of linear equations when the coefficient matrix is a non-Hermitian but symmetric complex matrix.We focus on the scaled preconditioned splitting iterative methods generally and consider the systems(1.2)whenP=(α-βi)Iwithα,βare both real numbers in this study.Theoretical analyses show that the new methods are convergent under the reasonable conditions,and the optimal parameters and spectral radius properties of the iteration matrix are discussed.Finally,numerical results are presented to show their feasibility and efficiency.
Here are some essential notations and preliminaries.As usual,we use Cn×nto denote then×ncomplex matrices set and Cnthen-dimensional complex vectors space;Rn×nto stand for then×nreal matrices set and Rnthen-dimensional real vectors space.X*represents the conjugate transpose of a matrix or a vectorX,andXTrepresents the transpose of a matrix or a vectorX.
A matrixA∈Cn×n(A∈Rn×n)is called Hermitian(symmetric)positive definite(or semidefinite),denoted byA≻0(or≽0),if it is Hermitian(symmetric)and for allx∈Cn,x/0,x*Ax>0(x*Ax≥0)holds true.Re(x)and Im(x)represent the real and imaginary parts of a complex numberx,respectively.The spectral radius of a matrixAis denoted byρ(A).Σ(A)represents the spectrum set of a matrixAandκ(A)stands for the condition number of a matrixA.
A=M-Nis called a splitting of a matrixAifM∈Cn×nis nonsingular.This splitting is called a convergent splitting ifρ(M-1N)<1.
The rest of the paper is organized as follows.Two scaled preconditioned splitting iterative methods are proposed in Section 2 and their convergence are discussed.Numerical experiments and comparison to other methods are shown in Section 3.Finally,we end the paper with a concluding remark in Section 4.
2.The Scaled Preconditioned Iterative Methods
First of this section,the new methods were introduced for solving a class of the system of linear equations when the coefficient matrix is a non-Hermitian but symmetric complex matrix,as shown in(1.1).
Letα,βbe both real numbers andαβ>0.Then we consider the preconditioned systems(1.2)whenP=(α-βi)I,that is the form as follows

Method 2.1The scaled preconditioned splitting(SPS)iterative method
LetMP=αW+βT,NP=i(βW-αT).Then the fixed point iterative method for solving the preconditioned system(1.2)can be written as

Alternatively,the system(1.1)can be solved iteratively based on the splittingA=Mα,β-Nα,βwith

And the iteration matrix is
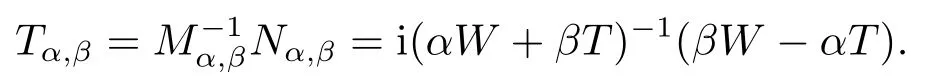
Method 2.2The flexible-scalar preconditioned splitting(f-SPS)iterative method
In Method 2.1,α,βare both real numbers,and are given in advance.To significantly speed up the convergence of the iterative methods,it is desirable to determine or find an accurate approximation to the optimal values ofα,β.So we concentrate on the generalized SPS iterative method with the flexible-parameters.Again motivated by the optimization models[12],the scaled parametersαk,βk,k=1,2,···,are generated by the minimizing the residuals at each step.The method is then designed as follows:
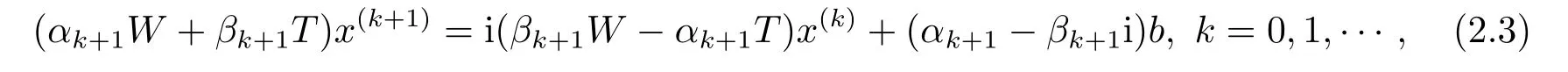
where
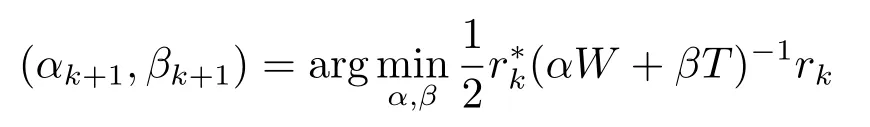
withrk=b-Ax(k),k=0,1,···.
Next,we discuss the optimal parameters and the spectral radius properties of the iteration matrix for the SPS Method,and study the convergence of Methods 2.1-2.2 addressed above.
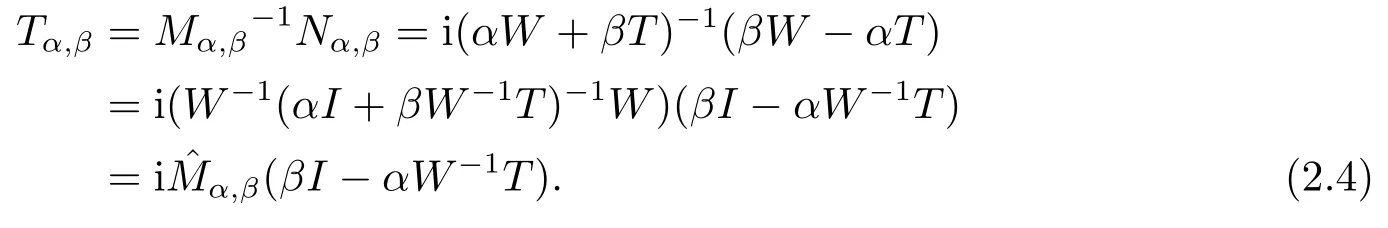
For the sake of simplicity,we can assume thatα,βare both positive real numbers without loss of generality.
Theorem 2.1LetA=W+iT∈Cn×nbe a non-Hermitian but symmetric matrix(=AT)withW,T∈Rn×nare both symmetric,andWbeing positive definite andTpositive definite or semidefinite.Letα,βbe both positive real numbers andλminandλmaxbe the extremal eigenvalues of the matrixW-1T.Then the following statements hold true:
(i)the spectral radiusρ(Tα,β)in the SPS method is not more than

(ii)the sequence{x(k)}generated by Method 2.1 converges to the unique solutionx*of the linear systems(1.1)for any initial guess if
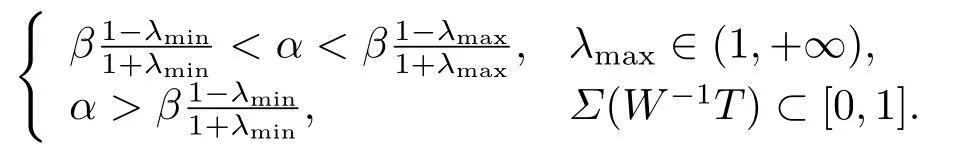
In particular,the iterative scheme(2.1)is convergent ifα>β>0 for the case thatTis a positive semidefinite matrix.
Proof(i)By(2.4)and direct calculations,we have
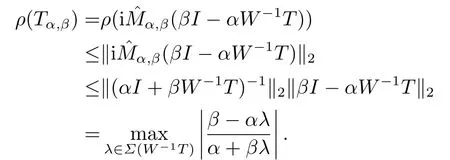
In the last step,the equality holds becauseW-1Tis a symmetric positive definite matrix,and so is(αI+βW-1T)-1.
It is known thatλis nonnegative.By introducing the following function:
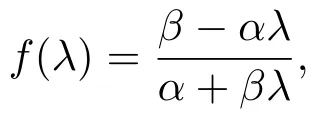
it is obtained thatf(λ)is a decreasing function with respect toλsincef′(λ)=Thus,the upper bound ofρ(Tα,β)given in(2.5)is obtained.
(ii)For the case thatλmax>1,δα<1 is equivalent toby simple calculations.And thenρ(Tα,β)<1,so the sequence{x(k)}generated by Method 2.1converges to the unique solutionx*of the linear systems(1.1).
For the case thatΣ(W-1T)⊂[0,1],thenλmax≤1 at that time.Thus,δα<1 is only equivalent toα>.
It is well-known thatλmin=0 ifTis a positive semidefinite matrix.And thenρ(Tα,β)≤α-1,the iterative scheme(2.1)is convergent ifα>β.
The proof is completed.
Corollary 2.1Assume that the conditions of Theorem 2.1 are satisfied,then the optimal relation between two parametersα,βthat minimizes the upper boundδα,βof the spectral radiusρ(Tα,β)is given by

ProofBy introducingτ=α/β,and
we have

Theng(τ)andh(τ)are respectively decreasing and increasing functions with respect toτ.It is deduced thatδα,βattains its minimum wheng(τ)=h(τ),which is equivalent to
That is to say,(2.6)holds true.
Theorem 2.2LetA=W+iT∈Cn×nbe a non-Hermitian but symmetric matrix(AA*,A=AT)withW,T∈Rn×nbe both symmetric,andWbeing positive definite andTpositive definite or semidefinite.Thenρ(Tα,β)<1 if for allx∈Cn,it holds that.
ProofLetλbe an eigenvalue of the matrixTα,βandxthe corresponding eigenvector,i.e.,=λx,or equivalently,λ(αW+βT)x=i(βW-αT)x.Then we have from the assumptions that

We obtainα>by direct calculations under|λ|<1.The theorem is proved.
RemarkIt is implied that all eigenvalues of the matrixTα,βlie in linearly imaginary axis from Theorem 2.2.
At the last of this section,a property of the matrixcan be given.
Theorem 2.3LetA=W+iT∈Cn×nbe a non-Hermitian but symmetric matrix(A/A*,A=AT)withW,T∈Rn×nbe both symmetric,andWbeing positive definite andTpositive definite or semidefinite.Assume thatλis an eigenvalue of the matrixdefined by(2.2),then Re(λ)=1.
ProofLetλbe an eigenvalue of the matrixandxthe corresponding eigenvector with‖x‖2=1.It is known that
So,
From assumptions,x*Wx>0,x*Tx≥0.Then we have Re(λ)=1.
3.Numerical Experiments
In this section,some test problems are provided to assess the feasibility and effectiveness of Methods 2.1-2.2 in terms of the numbers of iterations(denoted by IT),computing time(in seconds,denoted by CPU),and the residual(denoted by RES).The performance of Methods 2.1-2.2 in comparison with the MHSS,SMHSS and f-SMHSS methods mentioned in Section 1.All our tests are started from zero vector,and terminated when the current iteration satisfied‖RES‖≤10-6.The iteration fails if the iteration number is up to 8000.
Example 3.1The linear systems(1.1)is of the form(W+iT)x=b,with

whereV=tridiag(-1,2,-1)∈Rm×m,Vc=V-e11∈Rm×m,e1=(1,0,···,0)T∈Rm,em=(0,···,0,1)T∈Rm.We take the right-hand side vectorbto beb=(1+i)A1 with 1 being the vector of all entries equal to 1.
Example 3.2The complex linear systems(1.1)is of the form
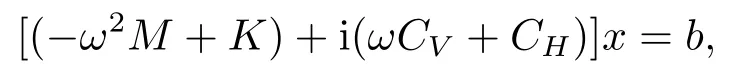
whereωis the driving circular frequency,MandKare the inertia and stiffness matrices,CVandCHare the viscous and the hysteretic damping matrices,respectively.We takeCH=μKwithμa damping coefficient,M=I,CV=10I,K=I⊗Bm+Bm⊗I,withBm=1/h2·tridiag(-1,2,-1)∈Rm×m,and mesh sizeh=Hence,Kis ann×nblocktridiagonal matrix withn=m2.In addition,we setω=π,μ=0.02,and the right-hand vectorbto beb=(1+i)A1 with 1 being the vector of all entries equal to 1.Furthermore,we normalize the system by multiplying both sides throughout byh2.
Example 3.3Consider the two-dimensional convection-diffusion equation

on the unit square(0,1)×(0,1)with constant coefficientηand subject to Dirichlet type boundary condition.By applying the five-point centered finite difference discretization,we get the system of linear equations(1.1)with the coefficient matrix
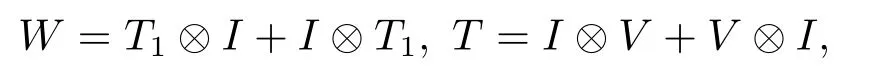
where the matricesT1,Vare given by
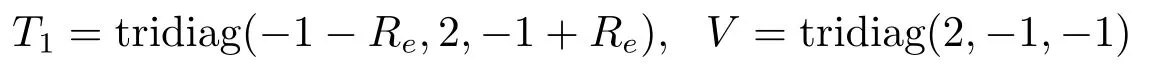
with
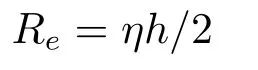
being the mesh Reynolds number,andh=1/(m+1)being the equidistant step-size.⊗denotes the Kronecker product.Moreover,the right-hand side vectorbis taken to beb=Ax*withx*=(1,1,...,1)T∈Rnbeing the exact solution.
In these experiments,we test matrices,with sizes up to almost 270,000(n=m2=512×512=262,144).Our numerical comparisons are reported in Tables 1-3.What we can see here is that Methods 2.1-2.2 work rather well.Among them,Method 2.2 needs the fewest numbers of iterations while Method 2.1 requires the fewest computing time.How to give consideration to both and so get a better method?This will be one of the subjects of our future research.
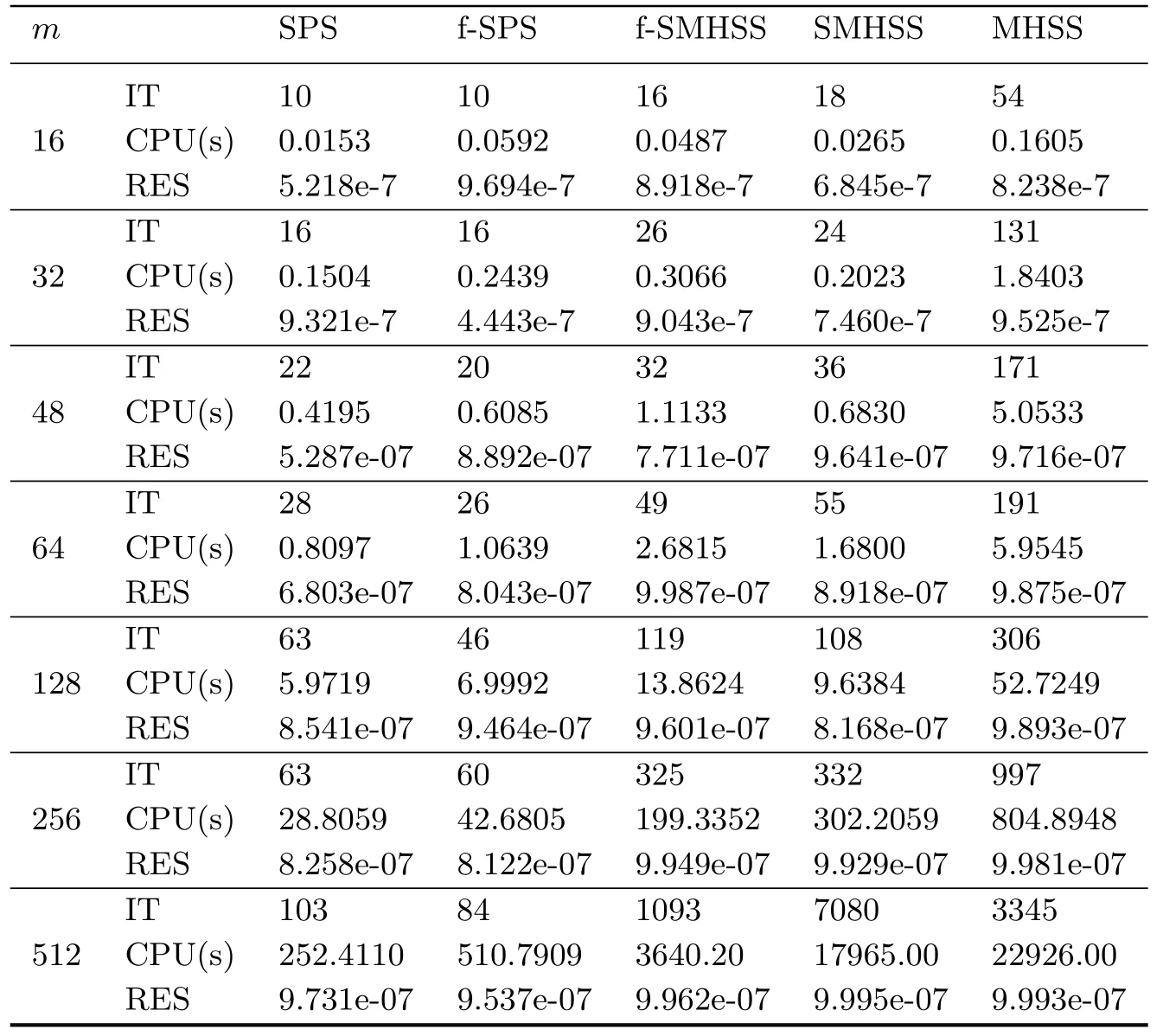
Table 3.1 The numerical results of these methods for Example 3.1

Table 3.2 The numerical results of these methods for Example 3.2

Table 3.3 The numerical results of these methods for Example 3.3
4.Concluding Remark
In this paper,we presented the scaled preconditioned splitting iterative methods generally for solving a class of complex symmetric linear systems,and studied the preconditioned systems when the preconditioned matrixP=(α-βi)I.Theoretical analyses show that the new methods are convergent under the reasonable conditions,and the formula between the optimal parametersα,βand the spectral radius properties of the iteration matrix are revealed in detail.Finally,we compared our algorithms against three existing ones from[10,12].Overall,numerical results are reported to show that Methods 2.1-2.2 are feasibility and efficiency comparably.
AcknowledgmentsThe authors gratefully acknowledge the anonymous referees for their helpful comments and suggestions which greatly improved the original manuscript of this paper.

