Hlder Estimates for a Class of Elliptic Equations Degenerate on the Boundary

SONG Qiaozhen(宋巧珍)，HUANG Yongpan(黄勇攀)

(1.School of Mathematical Sciences，Luoyang Normal University，Luoyang 471934，China;2.School of Science，Xi’an Polytechnic University，Xi’an 710048，China)

Abstract:The present paper investigates the Dirichlet problem for a class of elliptic equations degenerate on part of the boundary.By the construction of the barrier functions and the approximation by the polynomials we establish the pointwise Hlder type estimates for the solutions.

Key words:Boundary degenerate;Hlder Estimate;Barrier function

1.Introduction

It has been widely studied since sixties of last century.The interior estimates of the solutions to(1.1)were studied when Hmander’s finite rank condition holds for the smooth vector fields[1－6].After that the estimates for the non-smooth vector fields were studied[7－10].For instance，WANG[10]considered the interior estimate of the following equation

whereσis an arbitrary positive real number.In this case the vector fieldsX={∂x，|x|σ∂y}are Hlder continuous and do not satisfy Hmander’s condition.

In addition to these results，the boundary degenerate elliptic operators arise in mathematical finance，the porus media，the mathematical biology and so on[11－14].The global regularities to the Dirichlet boundary value problem defined by a class of boundary degenerate elliptic operator were studied[13－14].Furthermore，HONG and WANG[15]studied the regularity of a class of degenerate elliptic Monge-Amp`ere equation

inΩ⊂R2withu=0 on∂Ω.By Legendre transformation the equation can be rewritten as a degenerate elliptic equation which can be simplified to

wherem＞1 is an integer，=R+×R，and R+=(0，∞).

In this paper we consider a general form of(1.3).LetΩbe a slab domain in，i.e.，Ω=(0，κ)×R.We study the regularity of the boundary value problem，

Hereσandlare nonnegative numbers，b1，b2，care constants andc≥0.One can see that(1.3)is a special case of(1.4)by taking that 2σis a positive integer andl=2σ-1.Lis in the form of(1.1)whenl=σ.The operatorLis degenerate on the boundary{x=0}whenσ＞0.

We will start with the special case that is the equation(1.4)without lower order terms，i.e.，b1=b2=c=0.This means that we are concerned with(1.2)in the half space{x＞0}.It is also the transonic flow on the elliptic side whenIn this case we have the following theorem.

Theorem 1.1Supposeusatisfiesuxx+x2σuyy=finΩandu(0，y)=φ(y)，u(κ，y)=φ(y)，then the following holds.

1)Let 0＜α＜1 whenk=0，1.Iff(x，y)∈L∞(Ω)，φ(y)∈andψ(y)∈Ck，α(R)，thenuMoreover，

whereCis a constant depending onα，k，κ;

2)Let 0＜α＜min{1，2σ}.Iff(x，y)∈andψ(y)∈C2，α(R)，thenu∈Moreover，

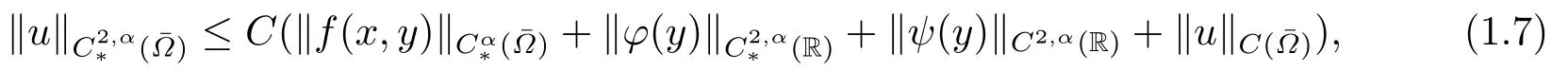
whereCis a constant depending onα，σ，κ.

After that the general form ofLu=fis considered whenl＞σ-1.By some modifications of the proof of Theorem 1.1 we have the similar result.

Theorem 1.2SupposeLu=finΩ=(0，κ)×R andu(0，y)=φ(y)，u(κ，y)=φ(y)，then(1.6)holds for 0＜α＜1 whenk=1 and(1.7)holds for 0＜α＜min{1，2σ，l}whenk=2，whereCis a constant depending onα，σ，l，k，b1，b2，c，κ.

The paper is organized as follows.In Section 2，we review the definition of the metric related to the vector fieldsX={∂x，|x|σ∂y}and the construction of the spaces such asIn Section 3，we derive the regularity of the special form to obtain Theorem 1.1.In Section 4，the regularity of the general equation is considered and the result of Theorem 1.2 is established by some modifications of the methods in Section 3.

2.Preliminaries

In this section，we review the function spaces and the results associated to the vector fieldsX={∂x，xσ∂y}[10].

Let us first recall the definition of the metric by

for any two pointsP1=(x1，y1)andP2=(x2，y2)in.There exists a constantγdepending onσsuch that

Define the ball with the center pointPby

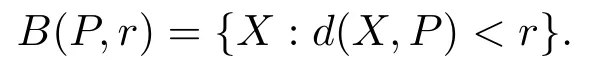
Next some useful function spaces related to the vector fields are provided.

For any 0＜α＜1，we define the Hlder space with respect to the distance defined in(2.1)as

Then we define the following quantities:

We also need the higher-order weighted Hlder spaces.

Definition 2.1We sayuis inifu，ux，xσuyare all inuis inifu，ux，xσuy，uxx，xσuxy，x2σuyyare all in(Ω).

To obtain the pointwise estimates we need the Campanato type spaces.As we know that Campanato space is embedding into the usual Hder space for the Euclidean metric[16].Then the similar embedding theorems have been obtain for vector fields of Hmander’s type or the doubling metric measure space[17－19].Here we need the following one.

Thekth order polynomial atX0=(x0，y0)is defined by

and

We remark that if we consider the point on the degenerate line，i.e.，Y0=(0，y0)，then some terms of thekth order polynomials atY0may disappear.More specifically，ifthena02=0 and ifσ＞αthena02=a11=0.Although some terms disappear，we still denote the second order polynomial as.

Definition 2.2We sayu∈atX0if for anyr＞0，there is a polynomialP(x，y)of orderksuch that

and we denote

wherePis taking over the set of polynomials atX0of orderk.

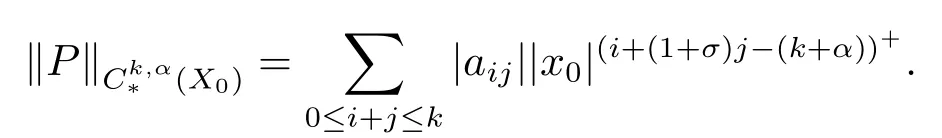
For a one-dimensional functionφ(y)，we use the distance function that is reduced by the function defined by(2.1)，i.e.，

We sayφ(y)isaty0if

To obtain the estimates we need the following scaling form.Let

So we define the intrinsic cube by

3.The Estimates for the Special Case

We start with the pointwise estimates on the boundary{x=0}.Since the equation is translation invariant inydirection，we only need to consider the original point.

Before we come to the proof of the theorems we give some lemmas.First we give the maximum principle for(1.4).

Lemma 3.1SupposeΩis a bounded domain in，andLu≤0 inΩ，u≥0 on∂Ω，thenu≥0 inΩ.

It is easily seen by applying the usual methods for the elliptic equations，so we omit the proof.

By calculating directly，we have the following lemma.

Lemma 3.2LetQ=(0，1)×(-2，2).Suppose

withu(0，y)=0，and|u|≤1，(x，y)∈∂Q，then

ProofBy Lemma 3.1 we know

We consider the function

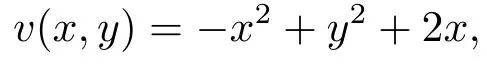
then

andv(0，y)≥0，v≥1 on=0.

Applying Lemma 3.1 to±u+vinwe have

especially，

Since the equation is translation invariant inydirection，we have

Lemma 3.3Let

andu(0，y)=φ(y)，y∈(-1，1).There exist constantsandδsmall such that if

and

then

ProofLetv(x，y)satisfy

Then we have|v|≤1，(x，y)

Let

then

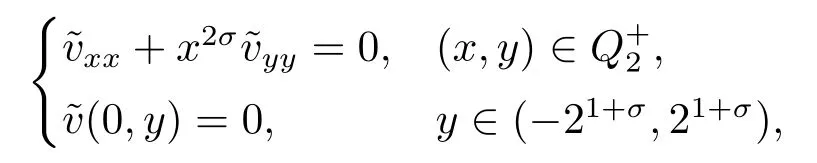
So

Letw=u-v.Thenwsatisfies

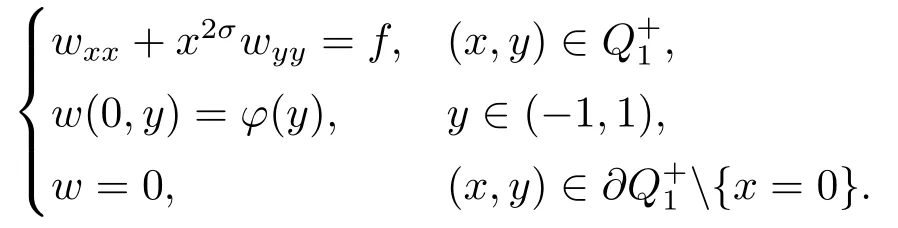
Leth(x，y)=Applying Lemma 3.1 to±w+h，we have

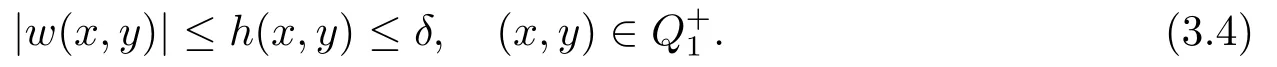
By(3.3)and(3.4)，we have

(3.2)can be obtained by takingsmall such thatand then takingThis completes the proof.

By Lemma 3.3 it is enough to prove the followingestimate at the original point.

Theorem 3.1Let 0＜α＜1，φ(y)beaty=0.Supposeuxx+x2σuyy=finandu(0，y)=φ(y)，thenuisat(0，0)and

whereCis a constant depending only onα.

The theorem can be proved by an inductive argument.

ProofWithout lose of generality we may assumeφ(0)=0，[φ]Cα*(0)≤δ，|f|≤δand|u|≤1.Otherwise one can consider

Thenu(x，y)satisfies the conditions in Lemma 3.3.So we have

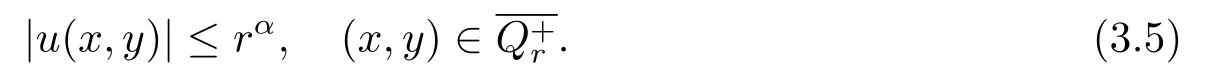
For every nonnegativek，we claim that

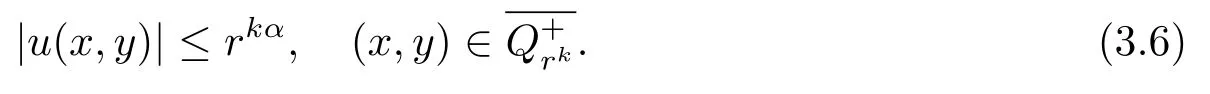
It is obvious that the claim holds fork=0，1.Assume(3.6)holds fork，then we prove the casek+1.Let

and

we have

Substituted byu(x，y)，it is easily seen that the claim holds fork+1.

For every point(x，y)there exists a nonnegative integerksuch that(x，y)∈Thus we have

so

In order to improve the estimates，we need the following Lemma.

Lemma 3.4Supposeuis a weak solution of

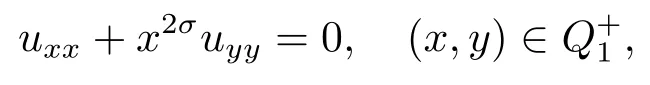
with the boundary condition

and|u(x，y)|≤1，(x，y)ThenuisC2，2σinand

This lemma can be proved by the odd extension and Lemma 2 in[10].

The following approximation lemma is the basic step to obtain the regularity on the boundary{x=0}.

Lemma 3.5Suppose

andu(0，y)=φ(y)，|u|≤1，(x，y)Then，for any 0＜α＜1，there exist constants 0＜r＜1 andδsmall enough such that if|φ(y)|≤δ，|f(x，y)|≤δ，then

and|a|≤C1.

ProofLetv(x，y)satisfy

Then we have|v|≤1.By the similar estimate as in Lemma 3.3，we have

and|a|+|b|+|c|≤C1.Sincev(0，y)=0，we knowb=c=0.By(3.8)and(3.9)，we have

by takingrsmall such thatand then takingδsmall such that.

By Lemma 3.5，we haveestimate ofuat(0，0).

Theorem 3.2Let 0＜α＜1，φ(y)beaty=0.Suppose

Thenuisat(0，0).Moreover，

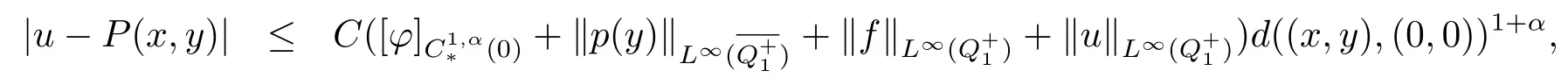
whereCis a constant depending only onα，P(x，y)is a first order polynomial at(0，0)andp(y)is a first order polynomial aty=0.

Notice thatφ(y)isaty=0.So we have

One can consider

then the proof is similar to Theorem 3.1，so we omit it.

By the similar proof of Lemma 3.5，we have the following lemma.

Lemma 3.6Suppose

and|u|≤1，(x，y)Then，for any 0＜α＜min{1，2σ}，there exist constants 0＜r＜1 andδsmall enough such that if|φ(y)|≤δ，|f(x，y)|≤δ，then there exists aP(x，y)such that

By this lemma，similarly，we obtain the following theorem.

Theorem 3.3Let 0＜α＜min{1，2σ}，φ(y)beat 0 andf(x，y)beat(0，0).Letusatisfy

Thenuisat(0，0)and

whereCis a constant depending onαandσ，P(x，y)is a second order polynomial at(0，0).

Right nowestimates at the original point are given.Next we give the proof of Theorem 1.1.

Proof of Theorem 1.1We assumeκ≥2，otherwise one can consider

By multiplying a small number，we can also assume

whenk=0，1，or

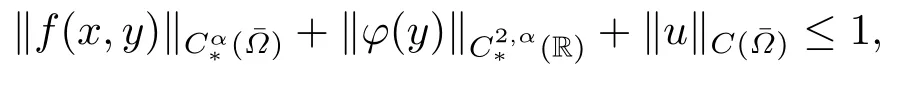
whenk=2.

Since the equation is translation invariant inydirection，we have the pointwise estimates of the point on the boundary{x=0}by Theorems 3.1，3.2 and 3.3.Now we give the estimate near the boundary{x=0}.

wherePY0(x，y)is akth order polynomial atY0and

Then

andv(x，y)satisfies

whenk=0，1，or

whenk=2.

By(3.14)，the equation is uniformly elliptic.The metric we defined is equivalent to the Euclidean metric inQ，we have

ThusvisCk+αand consequentlyvisat(1，0).So there exists akth order polynomialP1(x，y)such that

Substitutingvbyu，we have

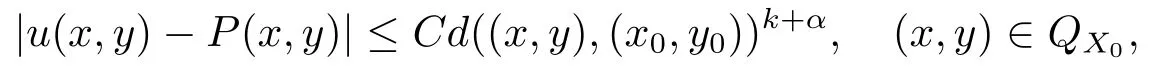
where

and it is easily to verify thatP(x，y)is akth order polynomial at(x0，y0).

Now let(x，y)∈ΩQX0.Thend((0，y0)，(x0，y0))≤d((x，y)，(x0，y0)).So

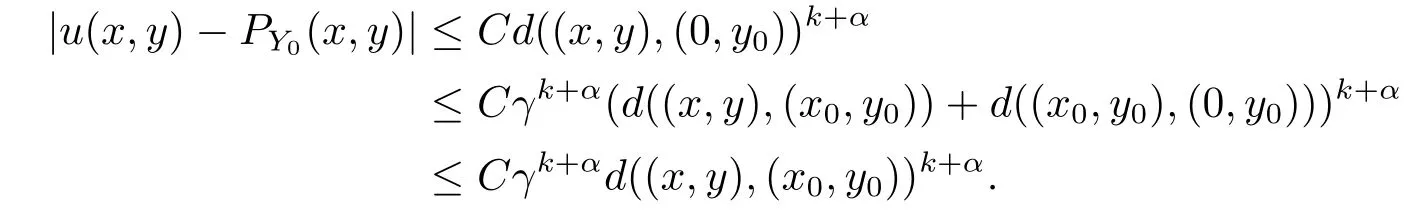
Thus we haveuisat point(x0，y0)forx0≤1.The estimate at any point(x0，y0)forx0＞1 can be obtained by the estimate of the uniformly elliptic equations.

4.The Estimates for the General Case

First of all we give the pointwise estimates of the point on the boundary{x=0}with some modifications of the lemmas and the theorems in Section 3.

Lemma 4.1LetA≥0 and 0＜δ≤1.Suppose

with

and

Then

provided that

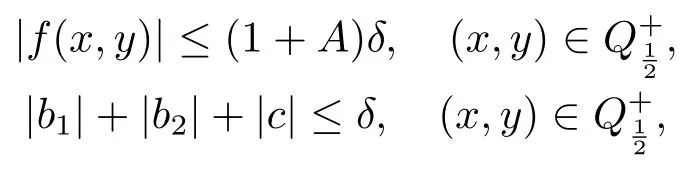
and

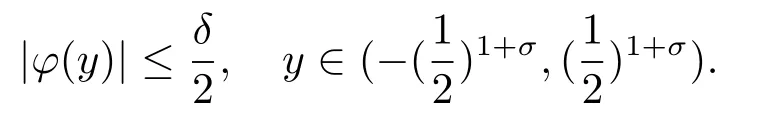
ProofLet

Then we have

and

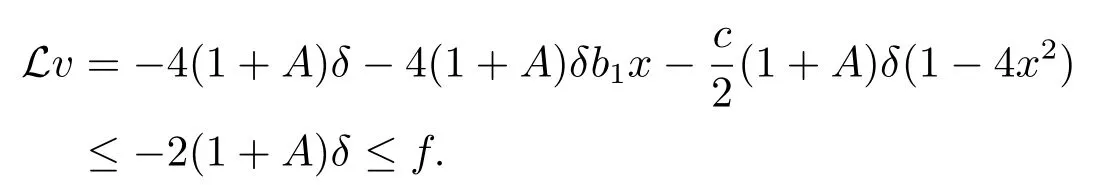
Applying Lemma 3.1，we have

The proof is finished.

With the aid of this lemma we have the following lemma which is similar to Lemma 3.5.

Lemma 4.2Suppose

withu(0，y)=φ(y)，and|u|≤1，(x，y)∈Then，for any 0＜α＜1，there exist constantsand 0＜δ＜1 small enough such that if

and

then

and|a|≤C1.

ProofLetv(x，y)satisfy

Then we have|v|≤1.Letw(x，y)=u-v，thenwsatisfies

By Lemma 4.1 we have

We also have

Sincev(0，y)=0，we knowb=c=0，and|a|≤C1.By(4.1)and(4.2)we have

by takingrsmall such thatand then takingδsmall such that

Applying Lemma 4.2 and an inductive argument we have the following theorem.

Theorem 4.1Letl＞σ-1，0＜α＜1，φ(y)beaty=0.Suppose

wherer0is a small positive number such that

Thenuisat(0，0)and

ProofWe will modify the proof of Theorem 3.1 to obtain this theorem.Sinceφ(y)isaty=0，we have

wherep(y)=a0+a1y.

Let

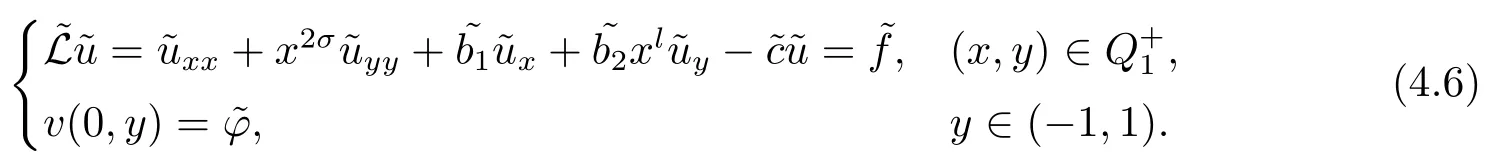
Here

and

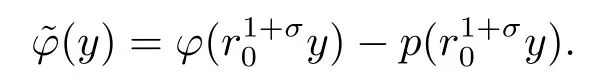
For our convenience we still denoteasLand so on.So we can assumer0=1 and

in(4.4).

By multiply a small constant we can also assumeandδ.Applying Lemma 4.2 we have

and|a1|≤C1.

We claim that

and

To prove this inductive step，we consider the function

Then

where

and

and|a|≤C1

Now substitutingˆubyu，we have

andak+1=ak+arkα.Then the claim holds.

Define

We have

So

Scaling back we have(4.5).The proof is finished.

Theorem 4.2Letl＞σ-1，0＜α＜min{1，2σ，l}，φ(y)beaty=0 andf(x，y)beat(0，0).Suppose

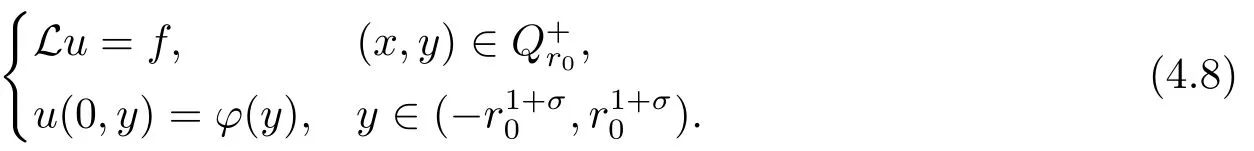
Thenuisat(0，0)and

Theorem 1.2 can be obtained by Theorem 4.1，4.2 and the similar argument of Theorem 1.1，so we omit the proof.