立足核心素养，提高“数列”教学实效性

江苏省盱眙中学 晋万里

一、教师适当引导，自主抽象出概念和规律

透过事物的物理属性，抽象出数学的概念和规律，这一思维过程便称为数学抽象。在高中数学“数列”教学中，教师应加强引导，让学生自主抽象出数列的相关概念，以促进学生数学抽象核心素养的形成。

例如，在学习“等差数列”一课时，笔者先根据闰年年份、鞋厂运动鞋码数、某列座位号顺序这三个情境写出三组数列：

（1）1880，1884，1888，1892，1896……

（2）35，36，37，38，39……

（3）30，27，24，21，18……

然后，笔者让学生认真观察以上数列，说出它们的共同特征。经过一番观察、计算和讨论，学生总结道：“这些数列的相邻两项都存在加法或减法的关系。比如，第一个数列中，每一项加上‘4’就等于下一项；第三个数列中，每一项加上‘-3’就等于下一项。”笔者表示赞许，并引出“等差数列”这一名词，接着提问道：“这样的数列被称为‘等差数列’，那么你能归纳这些数列的共性，并从中抽象出‘等差数列’的概念吗？”在问题的驱动下，学生开始给“等差数列”下定义，并反复斟酌字句，最终学生得出：“一个数列中的每一项减去它的前一项所得的结果一样，那么这个数列就是‘等差数列’。”学生的总结自然有些疏漏，于是，笔者再让学生对照课本上等差数列的定义进行补充和完善。通过这种方式，可以使学生更透彻地认识“等差数列”的内涵，并有效锻炼数学抽象思维。

二、创设推理情境，提高探究效率

所谓逻辑推理，就是从已有的事实出发，遵循一定的规则推导出新的结论。具备这一思维能力，有助于学生在探究新问题时得到更多启发，并能引导学生自主构建数学体系。所以，在高中数学“数列”教学中，教师可以通过设疑、留白、渗透类比思想等手段为学生创设推理情境，以加强对学生推理能力的锻炼，并让学生掌握数学探究的方法，提高学习效率。

三、引入实际问题，锻炼建模能力

以数学语言概括实际问题，以数学的知识和方法建立模型，进而解决问题，这一过程便是数学建模。所以说，数学建模是数学与现实生活相沟通的媒介，它体现了数学研究的价值。在高中数学“数列”教学中，教师可以适当构建真实的生活图景，引导学生利用数列解决实际问题，从而有效提高学生的数学建模核心素养。

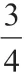
在审题过程中学生发现，从第2年到第6年，机器价值的变化呈等差数列；从第7年开始，机器价值的变化呈等比数列。于是，学生按照如下步骤构建模型、解析问题：设机器价值为an。

（1）当n≤6时，数列{an}是首项为100，公差为-10的等差数列，所以an=100-10（n-1）=110-10n；

最终，学生将以上结果进行综合整理，给该工厂负责人提供了机器价值的计算方法。之后，笔者再补充与本题相关的更新机器等情境，引导学生进一步探索和实践。通过以上方式，可以引导学生将数列与现实生活相结合，使其在认识数列价值的同时体会到数学应用的乐趣，最终促进学生数学实践能力的提升。

四、加强变式训练，提高运算素养

数列研究的是数的排列，所以在解决相关问题时，往往需要涉及大量的计算。虽然高中生具备一定的计算经验，但是数列习题变化多端，且公式繁杂，容易混淆，所以学生在计算过程中极易出错。因此，在高中数学“数列”教学中，教师不妨采取变式训练法，也就是变化问题中的非本质因素，引导学生不断转换思考和解题方法，借此强化学生思维的灵活性，提高学生的运算素养。

例如，在“数列”的基础性训练中，遇到这样一道例题：一个等比数列，Sn=48，S2n=60，则该数列前3n项的和是多少？

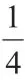
待学生完成解题后，笔者将该例题进行如下变式：一个等差数列，Sn=48，S2n=60，则该数列前3n项的和是多少？

这时，学生便需要转换思维，思考等差数列中Sn、S2n、S3n之间的关系，并通过推理、计算加以验证，然后再类比以上步骤进行解题。通过这种训练方式，可以有效提高学生的思维品质，并让学生在不断的推理、计算过程中熟练掌握数列的规律，最终提高解决数列问题的能力。

总之，在高中数学“数列”教学中，教师要根据数列的特点以及学生的实际需求适当融合核心素养，借此加强对学生数学相关的各方面能力的训练，从而提高数列教学的实效性。