以形助数，化难为易——“数形结合”在初中数学教学中的运用

江苏省海门中南东洲国际学校 王 姗

进入初中以后，数学学科愈发凸显“抽象”的特点，并在原有的认知基础上增加了较多的思维逻辑内容，逐渐提高了对学生的能力要求，促进学生学科思维的发展。在这一过程中，教师可借助“数形结合”，将原本抽象的知识变得生动形象，帮助学生更好地掌握与理解。本文将结合实例，从概念、代数及函数方面具体阐述“数形结合”在教学中的运用。

一、概念问题——把握要点，深化理解

在初中阶段，学生了解到的许多解题方法都是从基本概念衍生出来的。因此，在设计教学时，教师要关注学生对概念的理解，借助“数形结合”帮助学生明晰思路，使其在遇到相关问题时能灵活解决，以此提高解题效率，增强学生的数学学习信心。

在教学“平行线与相交线”一课时，课标要求学生掌握垂线的性质，即“直线外一点与直线上各点连接的所有线段之中，垂线段最短”。对于这一基本性质，在具体讲解时，教师可引导学生联系生活，寻找一些常见的垂线，由此作为切入点启发思考，在这一基础上进行建构，将熟悉的日常图形简化为数学线段，围绕概念展开细致的讲解。这样一来，学生在图形的帮助下就能清楚知道：垂直是两条直线的特殊位置关系，当两条直线相交所成的四个角中有一个角是直角时，即两条直线互相垂直，其中一条直线叫作另一直线的垂线，交点叫垂足，垂线段最短。

由此，教师能将教学内容生动形象地展现给学生，让学生在图的“支架”下巩固要点，并在后续练习中更灵活地思考，解决问题。

二、代数问题——明晰思路，提高效率

代数问题是初中数学学习的重难点，学生在练习及考试中不可避免地会遇到复杂的代数问题，经常要投入大量时间和精力分析，还未必能完全解决问题。对此，教师要在日常教学中渗透“数形结合”思想，帮助学生明晰思路，尝试将复杂问题简化，轻松得出答案。

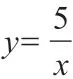
借助“数形结合”解决代数问题，不仅能缩短解题时间，给学生赢得更多机会，还能促进学生思考，在探索中发散思维，逐步获得发现。

三、函数问题——挖掘条件，发散思维

进入初中以后，学生开始接触函数问题，大部分学生对于问题中隐含条件的挖掘不到位，导致在解题时效率不高。对此，教师可引导学生运用“数形结合”的思想，为惯性思考提供助力，使学生在图形“支架”下对数学问题形成更全面的了解。

以“二次函数”的教学为例，很多学生在学习时就遇到了各种问题，分析这一现象，主要原因就在于其无法联系已有知识充分挖掘，以至于对问题的根本认识不到位，在解题时不全面，出现种种漏洞。针对这一问题，教师要借助“数形结合”改善。以这一题为例：二次函数y=x2+bx+c的图像与x轴相交于A、B两点，点A在原点左边，点B在原点右边，点P（1，m）（m＞0）在抛物线上，AB=2，tan∠PAB=1，求m的值以及二次函数解析式。在解决这一题时，教师可先带领学生分析题意，对每个条件进行理解，随后综合运用知识解决。在这一环节，教师可先尝试让学生独立思考，随后开展小组交流，让学生在合作学习中畅所欲言，积极表达自身想法，同时，教师要在教室巡视，认真倾听每个学生的想法，找准时机渗透“数形结合”思想，由此找到突破口，寻找最佳的解题方法。在这一基础上，教师可邀请小组代表发言，用自己的语言将解题思路表述出来，由此促进思维发散，让所有学生都清楚解题的步骤与方法。

借助这一过程，在一定程度上帮助学生简化函数问题，让其运用“数形结合”这个“秘密武器”赶走函数问题中的“拦路虎”。需要注意的是，大部分函数问题综合性比较高，难度较大，教师要适当强化对学生的引导，让学生在理解的基础上高效解题。

总之，“数形结合”是一种十分重要的数学思想，将其运用到各类问题中都能达到灵活、高效解题的目的。因此，在日常教学中，教师要潜移默化地渗透，促使学生掌握，在不断运用中提高把握能力，由此实现思维与能力的同步提升。