关于“角平分线的性质和判定”专题复习的研究

肖延举

摘  要：文章是对角平分线的性质和判定进行的综合应用研究，通过对角平分线知识的整体架构，引导学生发现问题、提出问题并解决问题。由对一个问题的思考角度和解决过程，总结出一类问题的解决策略，让学生真正学会思考、学会学习，进而提高解决问题的能力。教学中，要注意培养学生养成反思总结的习惯，使学生在反思中成长，不断进行自我完善。

关键词：角平分线的性质;角平分线的判定;对称性

本节课是继“角平分线的性质和判定”学习后的一节专题复习课，意在让学生体会角平分线的作用，感受角平分线的性质定理可以用来证明边相等，角平分线的判定定理可以用来证明角相等，根据角平分线的对称性，可以找到构造三角形全等的途径，从而解决证明线段和角相等的问题。通过本节课的学习，可以让学生积累添加辅助线解决问题的经验，为后续研究等腰三角形和四边形等相关内容做铺垫。

一、教学目标

（1）掌握角平分线的性质定理和判定定理，能利用角平分线的性质定理和判定定理解决问题。

（2）会利用角平分线的对称性构造全等三角形解决问题。

二、教学重、难点

教学重点：根据角平分线的性质定理、判定定理及对称性，探索构造全等三角形解决问题的方法。

教学难点：根据角平分线的性质定理和判定定理，添加辅助线来构造全等三角形，从而解决问题。

三、教學过程设计

1. 复习角平分线的性质和判定

（1）在△ABC中，∠C = 90°，AD是∠BAC的平分线，交边BC于点D，若CD = 5，则点D到AB的距离为_______。

（2）在△ABC中，∠C = 90°，∠BAC = 30°，点D为边BC上一点，过点D作DE⊥AB于点E，若CD = DE，则∠EAD的度数为_______。

【评析】通过这两道题目考查学生对角平分线的性质定理和判定定理的掌握情况，让学生体会定理的运用离不开作垂线段，为本节课探究典例做铺垫。

总结：角平分线的作用[ 性质→边相等; 判定→角相等; 一边一角→构造全等。]

2. 课堂探究

题目1  如图1，在四边形ABCD中，∠A = ∠B = 90°，DE平分∠ADC，且AE = BE，求证：CE平分∠BCD。

思路1：如图2，过点E作EF⊥CD于点F，利用角平分线的性质定理和判定定理解决问题。

当几何问题的条件中含有角平分线时，由角平分线的性质定理，可以想到向角的两边作垂线段来寻求线索，这是解决这类问题的常见策略。除此之外，此题还可以从全等的角度考虑解决。

思路2：如图3，在线段CD上截取DF = DA，连接EF，易证△ADE ≌ △FDE，再证Rt△EFC ≌ Rt△EBC即可。

思路3：如图4，延长DA至点F，使得DF = DC，连接FE，可证得△DEF ≌ △DEC。然后证明Rt△AFE ≌Rt△BCE即可。

【评析】思路2和思路3的本质是相同的，但是与思路1的思考角度截然不同。思路2和思路3是根据角平分线的对称性构造全等三角形，因为题目中给定了一个角平分线的条件，为三角形全等提供了一条公共边和一个相等的角，所以只需要再构造一条相等的边即可。构造与△ADE全等的三角形时，可将△ADE沿着DE翻折;构造与△DCE全等的三角形时，可将△DCE沿着DE翻折。

针对思路3，学生会发现FE和CE是共线的，善于思考的学生会猜想如果将辅助线的作法改为“延长CE和DA交于点F”，是否依然可以完成证明？答案是肯定的。同理，延长DE和CB交于点F，也是可以完成证明的。但是以上两种证明方法涉及等腰三角形的的相关知识，因此这里不做过多讨论，点到即可。

接下来，利用几何画板软件演示：对图1进行变换，令直线AB绕点E旋转，并且使∠A和∠B从90°的特殊角变换到一般情况，保证条件AD∥BC，思考上述结论是否依然成立？

变式：如图5，已知AD∥BC，DE平分∠ADC，且AE = BE，求证：CE平分∠BCD。

【评析】此题能激发学生进一步思考。学生需要意识到虽然图形发生变化，但是解题方法可能与题目1有共通之处，然后进一步创造条件解决问题，使学生感受数学问题中的规律性和解题策略的多变性。

思路1：如图6，过点E分别作EM⊥AD于点M，EN⊥DC于点N，EP⊥CB交CB的延长线于点P，再根据角平分线的性质定理和判定定理即可完成证明。

此题的条件中依然有角平分线，证明的结论依然是角相等，学生很容易想到利用角平分线的性质定理和判定定理来解决问题。因此，向角的两边作垂线段是多数学生的选择。除此之外，此题还有其他解法吗？学生会受题目1的启发，根据角平分线的对称性，通过截取边相等或者利用角相等构造一组三角形全等，若要证明角相等，只需要再证明另一组三角形全等即可。

思路2：如图7，在DC上截取DF = DA，连接EF，易证△ADE ≌ △FDE。通过观察图形，发现如果证明△CFE ≌ △CBE，即可解决问题。

目前这一组三角形满足的条件是“SSA”，不具备全等的条件，该如何解决呢？通过教师点拨，学生相互交流，共同找到如下的解决办法。

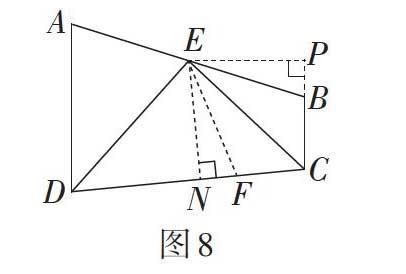
如图8，过点E分别作EN⊥CD于点N，EP⊥CB交CB的延长线于点P。易证△ENF ≌ △EPB。所以EN = EP。再利用角平分线的判定定理或者证明Rt△CNE ≌ Rt△CPE，即可证明结论。当然，证明△CFE ≌ △CBE也可以得到结论。

【评析】类比题目1，除了作垂直，学生易想到构造全等的方法，通过观察图形猜测两个三角形全等。但是给出的条件不够，这时教师抛出问题让学生自己去探索，发挥想象，更能激发学生的探究乐趣。

接下来，教师对变式题进行升华：把变式中的条件和结论提取为如下四个命题，选取其中的三个作为条件，一个作为结论，有几种选择？组成的命题是否成立？

（1）DA∥CB;

（2）DE平分∠ADC;

（3）AE = BE;

（4）CE平分∠BCD。

问题由封闭变为开放，使学生的思维更开阔、更灵活。共组成四个命题，两个同类型的已完成证明，再选取一个进行证明。

题目2  如图9，在四边形ABCD中，DA∥CB，DE平分∠ADC，CE平分∠BCD，求证：AE = BE。

通过上述题目1及变式，我们发现在涉及角平分线的题目中，可以充分利用角平分线的性质定理和判定定理向角的两边作垂线段，也可以利用角平分线的对称性构造全等三角形，常用的作辅助线的方法有截长、补短、作垂直、作延长线等。

3. 课堂检测

如图10，在△ABC中，∠ACB = 90°，∠B = 60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F。

（1）试探究FE和FD的数量关系。

（2）若∠ACB不是直角，其余条件不变，上述结论是否依然成立？若成立，给出证明;若不成立，说明理由。

四、教学反思

1. 题组设计由特殊到一般，由闭合到开放

本节课主要是针对“角平分线的性质和判定”进行的专题研究，专题研究就是从某一重要的数学知识、技能或数学方法加以展开、纵向深入，对知识和技能的内在联系及数学思想和方法进行较为深入的剖析，围绕某个典型例题对学生进行集中训练，从而让学生掌握这类问题的解决策略。

本节专题研究课由一道典型例题引入，其具备一定的特殊性，即有两个角是90°，对这道题目的探究，学生提出了多种多样的解法，教师要对学生的想法加以鼓励，培养学生勇于探究的精神，随后对题目1进行变式，即將原来的特殊角改为一般角，但是结论依然成立，让学生体会由特殊到一般的数学思想方法。最后，对本节专题进行升华设计，把题目及变式中的题设和结论全部提取出来，自由组合成新的命题，让学生对新命题是否成立进行猜想和验证。这种设计使问题由闭合到开放，能够有效培养学生敢于猜测、质疑的精神，让学生体会问题的多变和方法的不变性，更能激发学生探索的乐趣，最终总结出一类问题的解决策略，使学生认识到数学的本质。

2. 关注学习过程，注重数学思维的培养

一堂课的好坏，不是看教师教了多少，而是看学生学到了多少。因此，教学时，教师不只要教会学生解决问题的方法，更重要的是培养学生的思维能力。本节专题复习课设计的题目，首先考查学生对角平分线的性质定理和判定定理的掌握情况，但是学生的思维不能被固化，要了解见到角平分线不仅有向角两边作垂线段这一种解决问题的方案，还可以利用角平分线的对称性构造全等三角形来解决问题，使学生的思维更加开阔。在对方法进行探究时，教师不能急于求成，要留给学生充足的时间和空间，鼓励学生去大胆猜测和验证，注重学习过程，进而培养学生发现问题和解决问题的能力。

参考文献：

[1]王春春.“分式”（第1课时）教学设计及说明[J].中国数学教育（初中版），2017（7 / 8）.