核心素养下高中数学问题解决策略探微

山东省北镇中学 李 响

数学是一门理论结合实际的学科，对学生的思维意识、学习能力、学习技巧等都有较高的要求。高中生有很多想法，就会有很多解题思路，只有引导他们正确的学习方向，才能保证课堂教学的有效开展。

一、把握核心素养内涵，培养学生的问题解决意识

在培养学生的核心素养之前，教师要明白以下几个问题：“核心素养有哪些内涵？应该怎样培养学生的学习技能？当学生核心意识缺乏时，教师应该做什么？”只有从本质上出发，了解学生的真实诉求，才能制订有价值的课堂教学方案，为学生核心素养的形成保驾护航。

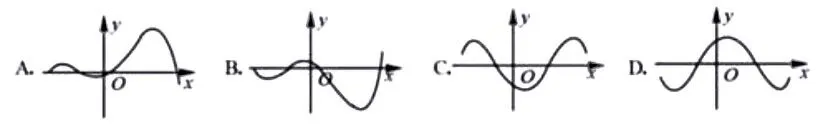
比如，上图中的四个函数图像，每个图像都有各自的特点和走向趋势，教师可以向学生提出问题，引发他们的思考，提高每个学生对数学知识的理解和运用能力。通过观察，我们可以看出，A图中的函数图像呈现先增后减，再增再减的趋势，而且函数图像与x轴有4个交点，即当y=0时，x有4个不同的值。对于每个图像的理解，不同的学生可能有不一样的看法，教师要多和学生沟通交流，明白他们的思想误区，引导他们走向正确的解题方向。

二、强化宏观学习过程，提升学生的问题解决能力

数学是一门基础性的学科，学生在小学和初中已经掌握了基本的理论和定理，只是缺乏实际的解题经验。教师的作用在于帮助学生解决问题，带领学生发现问题，在问题解决过程中形成能力，产生一个良性的学习循环圈。这种教学模式是合乎逻辑的，同时也能促进学生自主学习习惯的养成，优化课堂的教学进程。

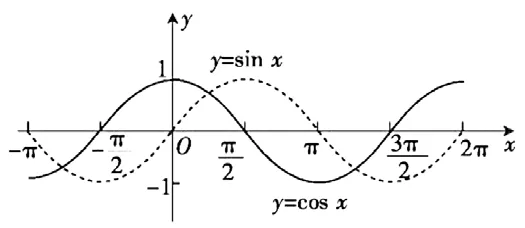
比如，在教学函数图像的过程中，教师可以把正弦函数和余弦函数的图像结合起来，这样更能吸引学生的学习兴趣，满足学生的求知欲望。无论是正弦函数还是余弦函数，它们的图像都与x轴有几个不同的交点。几何思路是一个重要的思路，不仅能扩展教学内容，还能促进学生对数学知识的理解和吸收，对于学习能力较强的同学，教师还可以应用数形结合的教学模式，引导学生发现问题、解决问题，培养学生的数学核心素养。

三、凸显例题课堂价值，保证学生的问题解决素养

例题是数学学习的灵魂，但很多教师认为数学教学就是“换汤不换药”，只要给学生一定的例题练习，就能提升他们的核心思维能力，这种想法是不对的。例题不单要在模式上创新，还要在素材上创新，这样才能引导学生建立全面的理解，学会根据不同的数学例题整理不同的学习思路，自主提升数学素养。从更为学术的角度来看，每个学生的学习环境不同，所面临的学习挑战也不同，教师不能只给他们提供单一的数学例题，而是要从多角度出发，让数学课堂的内涵变得更加丰富，让学生的学习生活变得更加多彩。

在“向量”这一模块的教学中，很多学生不理解向量的本质概念，我们就可以应用实际例题引导学生思考，用几何图形解释向量的产生过程，尤其是涉及“三角形法则、平行四边形法则”等的运用时，向量就是一个重要的数学工具， 能帮助学生理解图形中的线条性质，找到重要的解答思路。教师要指导学生正确区分“向量”和“线段”的区别。线段没有方向，只有两个端点和线，而向量是矢量，是有方向的射线。对于等边三角形来说，三条线段彼此所形成的夹角都是60°，类似的图形还有等腰三角形、等腰梯形等，它们两个底角所形成的向量角都是一样大的。

从素质到素养，很多人都以为只是一字之差，实则不然。对学生核心素养的培养，需要经历一个循序渐进的过程，并非一件轻而易举的事情。特别是高中数学课堂中，教师要多和学生沟通交流，通过有效的途径来培养学生的核心素养，发挥有价值的教学优势。当学生意识到核心素养的重要性时，便能积极配合教师的课堂教学，转变自己的学习模式，从本质上提升数学学习能力。