基于薄层单元模型的弹体与引信系统螺纹连接参数确定方法
鄢阿敏,皮爱国,王健,黄风雷,王晓锋
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.北京系统工程研究所,北京 100034)
0 引言
螺纹连接具有强度高、连接可靠、拆卸方便等优点,是组合结构里一种广泛应用的连接形式,侵彻弹体与引信的连接形式一般为螺纹连接。在硬目标侵彻过程中,弹体与引信螺纹连接的状态直接影响着引信体过载响应情况。对于组合系统动态响应的研究,有限元仿真技术作为一种快捷、有效的手段,可以为试验提供准确的指导,已被科研工作者广泛的应用。因此,探索出一种有效的仿真手段来准确、合理模拟螺纹连接,对于分析弹体与引信系统振动响应特性意义重大。
针对螺纹连接有限元模拟方法,大量学者开展了相关方面的工作。Chaaban等[1]运用有限元建模方法对螺纹连接进行参数化分析,研究第1活跃螺纹牙处应力集中对整个螺纹连接疲劳寿命的影响。Zhang等[2]通过建立实体螺纹的方式研究弹体与引信螺纹连接界面的碰撞过程,获得螺纹连接的碰撞频率。Zheng等[3]通过建立实体螺纹研究螺纹组合结构在冲击条件下的松动行为。上述针对螺纹连接的研究均是基于螺纹接触界面非线性接触算法进行分析的。
此外,有限元软件进行模态分析时,难以处理螺纹接触引入的非线性特征,导致非线性接触算法在模态分析中难以适用。早期研究就如何准确表征连接界面这一问题进行大量探索,尤其集中在薄层单元法应用上。Desai等[4]1984年首次提出薄层单元建模概念,通过赋予薄层单元法向接触刚度与剪切刚度来表征岩石与土壤接触界面。随后一些学者将其应用于模拟螺栓[5-6]与螺纹[7]连接界面,使仿真计算精度有了显著提高。然而在薄层单元建模过程中,准确确定薄层单元的参数是关键,现有研究中对薄层单元材料参数的确定均是依赖试验,给薄层单元法的推广带来了不便。
Gaul等[8]通过试验获取薄层单元相关材料参数,并将薄层单元应用于发电机双盘转子收缩接头有限元模型中,获得与试验一致的响应特性。Bograd等[9]采用薄层单元模拟多螺栓连接,并设计试验获得螺栓连接的阻尼参数与刚度参数,将其应用到薄层单元模型中,取得了显著的效果。Schmidt等[10]通过一般试验推导出薄层单元材料参数,应用于研究钢组合结构的振动与阻尼特性,数值模态分析结果与试验模态结果吻合较好。以上研究是直接利用试验来确定薄层单元材料参数。还有一些研究是基于模态试验结果对薄层单元的参数进行优化识别,获得薄层单元材料参数。如Adel等[11]提出双薄层单元模型模拟混合结构中螺栓连接界面的方法,通过模态试验的结果对上、下两层薄层单元的材料参数进行识别,使模型可以准确预测试验结果。Alamdari等[12]将薄层单元引入通过螺母接口连接螺纹管的有限元分析中,通过模态试验获得的频响曲线对薄层单元的材料参数进行优化识别,该方法显著减少连接建模中的不确定性。Zhao等[13]采用薄层单元模拟螺栓连接接触刚度,并利用螺纹连接组件不同预紧力下的模态频率对薄层单元的接触刚度进行识别。综上所述,采用薄层单元模拟组合结构的接触界面,薄层单元材料参数一般通过试验直接获得,或者基于试验结果对薄层单元的材料参数优化更新获得,这两种方式存在明显的缺点:均依赖于试验,从而使薄层单元的应用变得复杂。鉴于此,本文基于理论推导提出薄层单元材料参数的确定方法,并将薄层单元建模的方式应用于模拟弹体与引信螺纹接触,使螺纹连接薄层单元的参数确定不再高度依赖于试验,提高薄层单元仿真计算的效率。
本文基于螺纹连接弹性模型探索螺纹连接刚度的计算方法,推导出薄层单元弹性模量与剪切模量的计算公式,并将所获得材料参数应用到仿真模型中;通过模态试验验证薄层单元参数的准确性,并对相关变量开展深入研究,取得了预期效果,旨在为类似的研究工作提供一定的指导作用。
1 螺纹连接刚度的研究
1.1 螺纹连接轴向刚度的确定
图1为螺纹连接示意图,分为螺母、螺栓、螺纹3个部分,螺纹是连接螺栓与螺母的重要环节,螺栓与螺母的相互作用通过螺纹来传递。图1中Fa为螺纹连接所受的轴向力,FB为第1扣螺纹牙的轴向力,l为螺纹连接旋合长度。在螺纹承载分析的解析法中,Sopwith法[14]与Yamatoto法[15]两种解析方法得到了较为广泛的认可,两种方法类似,都将螺纹看成悬臂梁,并且以螺纹轴向载荷分布反映螺纹承载的分布。Zhang等[16]在此基础上,考虑螺纹连接加载分布,提出一种更为准确的螺纹连接刚度计算方式,并取得良好的结果,本研究也是基于此理论来开展的,具体表达式为
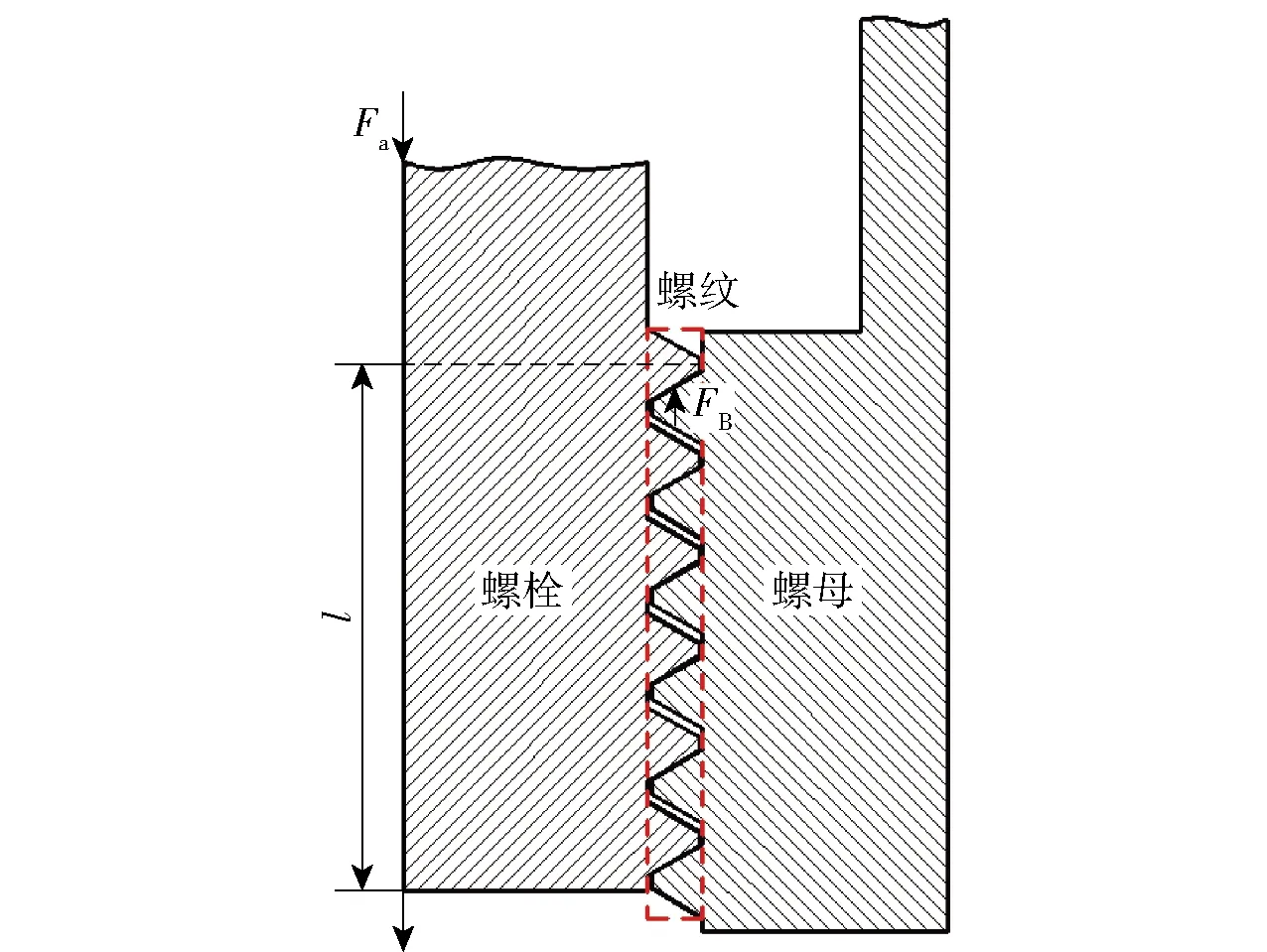
图1 螺纹连接示意图
(1)
式中:Eb和En分别为螺栓与螺母的弹性模量;Sb和Sn分别为螺栓与螺母的横截面积;λ为自定义的变量,
(2)
kba和kna分别为螺栓与螺母上螺纹单位长度的轴向刚度,
(3)
δba、δna分别为螺栓与螺母轴向总变形,β为螺纹的导角。Zhang等[16]推导出不考虑螺纹牙接触摩擦力情况下δba与δna的计算方法;Lu等[17]提出考虑螺纹牙连接摩擦力δba与δna的计算方法。
(1)式是计算轴向刚度的关键理论部分,可知轴向刚度的大小取决于螺距、旋合长度、螺纹材料、螺纹牙接触摩擦系数等多种因素。在试件设计过程中,螺距与旋合长度更易于精确控制与对比,因此选择螺距、旋合长度两个重要变量进行相应仿真与试验研究。轴向刚度的精确计算为后续薄层单元剪切模量的确定提供了理论支撑。
1.2 螺纹连接径向刚度的确定
文献[16]中给出螺纹连接轴向载荷力分布,其表达式为
(4)
螺纹连接第1扣螺纹所受的力最大,然后逐渐减小。螺纹通过互相接触传力,所以径向力的分布规律与轴向力的分布规律一致。根据径向变形与轴向变形之间的关系可得,螺栓与螺母径向总变形分别为
(5)
式中:α等于1/2的螺纹牙顶角。
螺栓与螺母单位长度的径向刚度表达式分别为
(6)
代入(1)式和(2)式即可得出螺纹连接的径向刚度Kr.
2 薄层单元基本原理
2.1 薄层单元表征方式理论分析
采用薄层单元模拟螺纹连接接触面。薄层单元尺寸l×s×t,其中s为薄层单元圆周长度,t为薄层单元的厚度。根据虚位移原理得
δW=∭V{σ}T{δε}dV=δ{u}TK{u},
(7)
式中:V为薄层单元在局部坐标系下的体积;σ为单元的应力;ε为单元的应变;{u}为节点位移;K为单元刚度矩阵。
图2为薄层单元等参变换,通过等参变换计算薄层单元刚度矩阵K:
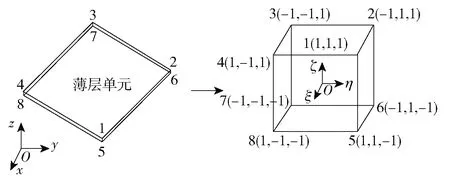
图2 薄层单元等参变换
(8)
式中:B为变换矩阵;D为本构矩阵;ξ、η、ζ为自然坐标;J为雅克比矩阵,表征局部坐标与自然坐标的偏微分关系,在自然坐标系下,数值积分形式更简便,可以将雅克比矩阵J进一步简化为
(9)
(9)式代入(8)式,可得到薄层单元刚度矩阵K的数值计算表达式:
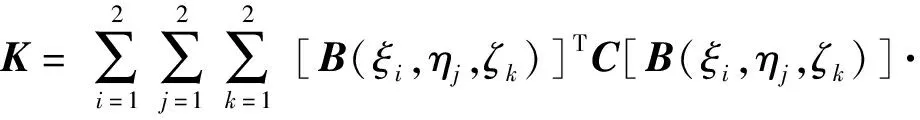
det([J(ξi,ηj,ζk)])wζ,iwη,jwξ,k,
(10)
式中:C为本构矩阵;wζ,i、wη,j、wξ,k为高斯积分权函数[18-19]。
对于薄层单元,薄层单元的厚度t远远小于另两个方向的特征尺寸l和s,根据Desai等[4]的描述,假设采用泊松比为0的材料本构关系时,薄层单元法向刚度与切向刚度将会解耦,单元的面内应变分量(εx,εy,γxy)和应力分量(σx,σy,τxy)将被忽略。若接触的法向{e}n和两个切向{e}t分别定义为薄层单元局部坐标系的z轴、x轴、y轴方向,根据上述分析,连接界面法向与切向接触性能相互独立,两个切向的接触性能具有良好的一致性,表征界面接触性能的薄层单元本构方程为
(11)
式中:σn为法向应力;τtx、τty分别为x轴、y轴方向的切向应力;Esn、Gst分别是薄层单元的法向弹性模量和切向剪切模量;εn为法向应变;γtx、γty分别为x轴、y轴方向的切向应变。
在有限元计算中,若采用各向同性材料模拟薄层单元,各向同性材料仅有弹性模量Es和剪切模量Gs两个独立的材料参数。根据薄层单元的基本理论,εx=εy=εxy≈0,材料的本构方程为
(12)
2.2 薄层单元材料参数确定
2.2.1 薄层单元轴向刚度分析
图3(a)为薄层单元受轴向力变形示意图,其中τ为受轴力后产生的剪切应力,可知
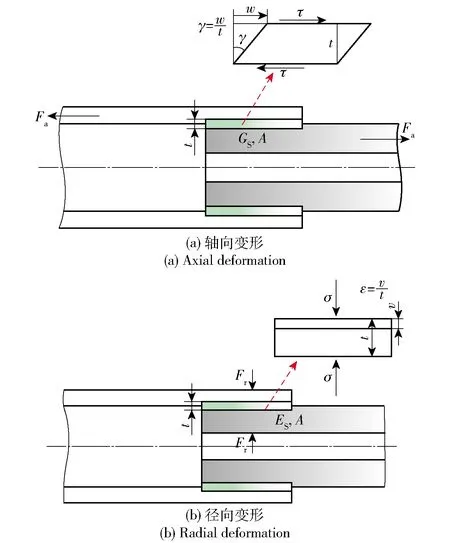
图3 螺纹连接薄层单元变形示意图
(13)
式中:γ为剪切角;A为接触面积;w为轴向位移。
对(13)式进行变换,可得
(14)
式中:Ka为螺纹连接的轴向刚度。
根据(14)式与(1)式薄层单元的剪切模量Gs可以表示为
(15)
式中:λa为自定义变量,由(2)式计算可得。
2.2.2 薄层单元径向刚度分析
如图3(b)为薄层单元受径向力变形示意图,Fr为螺纹所受的径向力,径向力作用下产生的法向应力可以表示为
(16)
式中:v为法向位移。
对(16)式进行变换,可得
(17)
由(17)式与(1)式,薄层单元的弹性模量可以表示为
(18)
式中:λr为自定义变量,由(2)式计算可得。
综上可得,薄层单元模拟螺纹连接的关键是要准确确定薄层单元的材料参数。首先由(1)式计算出螺纹连接的轴向连接刚度Ka与径向连接刚度Kr,然后利用(15)式与(18)式计算得出薄层单元的剪切模量Gs与弹性模量Es.
3 模态试验研究
3.1 螺纹管组合件模态试验
为验证所确定薄层单元材料参数的准确性,开展了螺纹管连接件的模态试验。试件由两段空心圆柱管通过螺纹连接组成,相关尺寸如图4(a)所示,共设计5组螺纹试件,如表1所示。此外,设计同尺寸无螺纹试件同组进行试验,如图4(b)所示。
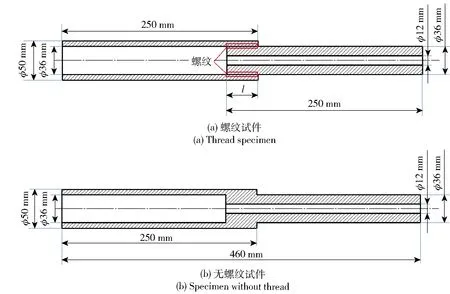
图4 试验试件
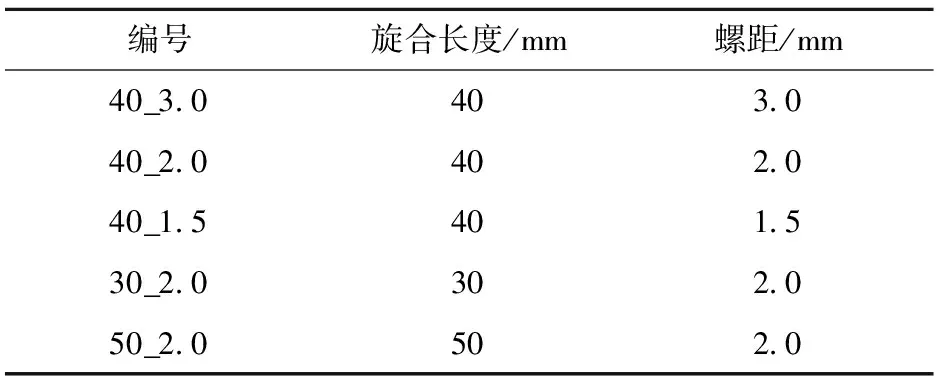
表1 螺纹试件几何尺寸
田晶等[20]采用多种悬挂方式与弹性支撑方式进行自由模态试验,表明采用弹性绳悬挂的方式最接近自由边界状态,参考其方法,本文采用弹性绳悬挂来模拟自由边界条件。利用电磁激振器对试件进行激励,图5为激励点与测量点位置示意图,激励点选择在Z1位置处,2个美国PCB公司三向加速度传感器分别粘贴在试件的A1与A2位置。利用比利时LMS公司的模态分析软件进行辅助测量与分析,1个16通道的模态分析仪用于接收和处理信号,采样频率设置为20.48 kHz.模态分析仪产生的扫频信号经过运算放大后输入电磁激振器,激振器接收信号产生激振力,激振器连接杆端部安装有力传感器,采集激振力输入模态分析仪中,形成对激振力的反馈回路控制,使激振力保持在稳定的激励水平。
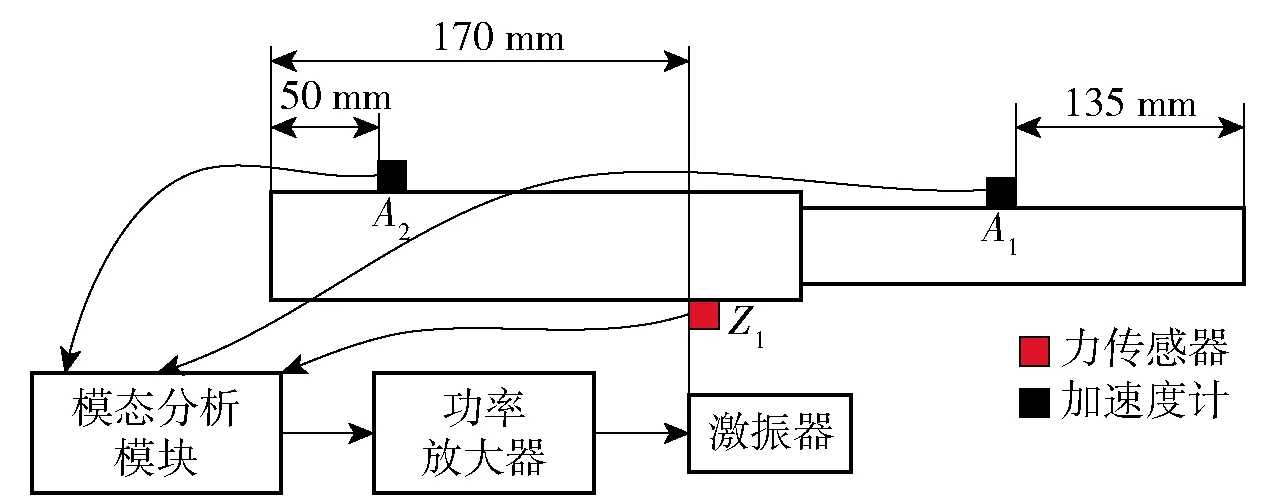
图5 激振器与传感器分布示意图
试验中选择正弦扫频信号为激励信号,该类正弦扫频信号可以保证测试的重复性,能够很方便地测出模态频率与频响曲线。扫频范围为100~5 000 Hz,保证扫频范围能够覆盖结构前3阶模态频率,扫频速度为5 Hz/s,激励力的幅值为0.1 N.试验测得的旋合长度40 mm无螺纹试件前3阶固有频率,如表2所示。此外,为与试验结果进行对比,对旋合长度40 mm无螺纹试件进行仿真计算,结果如表3中L40行所列。对螺纹试件的测量采用分段扫频激励,激励频率分别为500~1 000 Hz、2 000~3 000 Hz、3 500~4 500 Hz,扫频速度为5 Hz/s,激励力的幅值为0.1 N,测量结果如表2所示。表2中40_3.0、40_2.0、40_1.5分别表示旋合长度40 mm,螺距3.0 mm、2.0 mm、1.5 mm的螺纹,30_2.0、40_2.0、50_2.0分别为旋合长度30 mm、40 mm、50 mm,螺距为2.0 mm的螺纹。
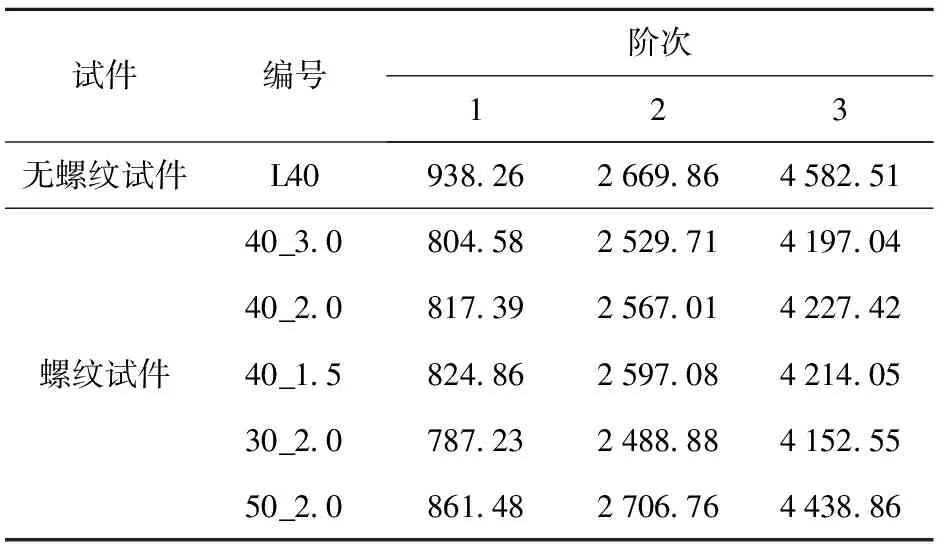
表2 螺纹试件与无螺纹试件模态试验获得的前3阶固有频率
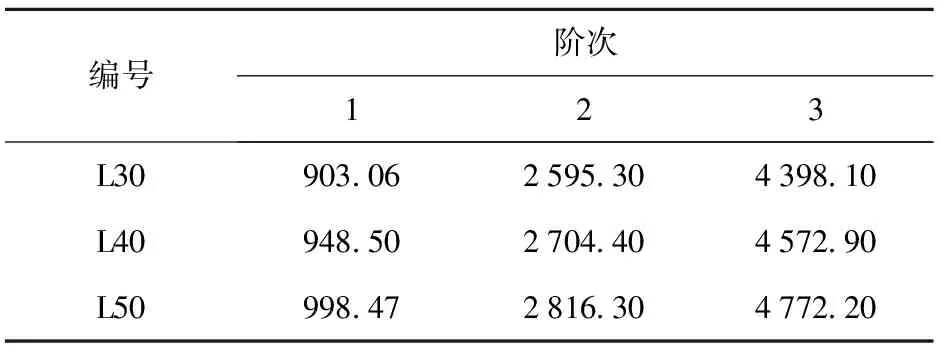
表3 无螺纹试件仿真计算获得的前3阶固有频率
由于未对旋合长度为30 mm与50 mm无螺纹试件进行模态测试,因此采用仿真结果进行代替,如表3中L30与L50两行数据所示。比较螺纹试件与无螺纹试件各阶模态频率可知,相比无螺纹结构,螺纹连接各阶模态频率均出现明显的下降,分析原因由于螺纹连接引入接触刚度与摩擦阻尼等非线性因素,相比较无螺纹结构,整体刚度降低,导致各阶模态频率下降,此外,摩擦阻尼的存在也会造成各阶模态频率下降。比较40_3.0、40_2.0、40_1.5模态试验结果可得,螺距变化对各阶模态频率影响不大,随着螺距减小,各阶模态频率增加,但增加幅度很小。比较30_2.0、40_2.0、50_2.0模态试验结果可得,随着旋合长度的增加,螺纹连接刚度增大,各阶模态频率均有明显的提高。
3.2 弹体与引信系统螺纹连接模态试验
弹体与引信螺纹连接主要由两部分组成:弹体和引信体。如图6所示,弹体与引信体、引信体的前后端盖与引信外壳的连接均采用螺纹连接。所测弹体与引信组合系统的模态频率较大,超出了激振器激励的范围,因此采用锤激法进行测量。为对弹体的材料参数进行验证,首先开展了弹体结构(不含引信)的模态试验。
采用弹性绳对试件进行悬挂模拟自由边界条件,1个美国PCB公司产三向加速度传感器粘贴在距弹尾100 mm的位置,传感器x轴、y轴和z轴方向的灵敏度分别为104.4 mV/g、102.3 mV/g和97.8 mV/g.利用比利时LMS公司的模态分析软件进行辅助测量与分析,1个16通道的模态分析仪用于接收和处理信号,采样频率设置为40.96 kHz.采用力锤对试件进行激励,选择x轴、y轴、z轴方向上试件任一个位置作为锤击的激励点,每一激励点处的测量结果可以相互补充,测量获得弹体以及弹体与引信组合系统的前3阶模态频率,如表4所示。
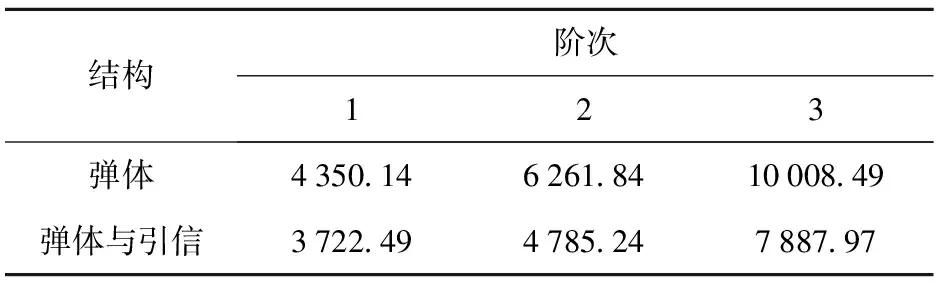
表4 模态测试结果
4 螺纹管薄层单元仿真研究
4.1 薄层单元厚度分析
Shokrollahi等[21]在研究中,将组合结构接触表面分别向两边法向方向进行扩展定义为接触影响区域,参考其研究成果,本文根据实际螺纹齿高分别向法向延伸t/2作为螺纹接触影响区域。采用厚度t的薄层单元模拟螺纹接触影响区域,薄层单元的长度为内外螺纹结合面长度。薄层单元厚度的选择对计算结果的影响较大,对薄层单元厚度定义比例系数[22]为
(19)
如文献[4]所描述,当R取值为10~100时能获得较准确的结果。
为了给薄层单元厚度选择提供依据,研究薄层单元厚度变化对仿真精度的影响。定义薄层单元厚度t与螺纹连接公称直径D比值为无量纲厚度t/D.当t/D取值变化时,对螺纹型号为M36×2-6H/6g-40的螺纹管进行建模分析。薄层单元的材料参数由(15)式与(18)式进行计算,螺纹管材料参数如表5所示,均采用线弹性材料模型进行模拟。表5中E为弹性模量,ν为泊松比,ρ为密度。

表5 材料参数
图7为t/D变化时前3阶模态频率f1、f2、f3的散点图。对离散点进行3次曲线拟合,拟合函数如图7中所示。由图7中拟合曲线可知,当t/D处在区间[0.08,0.18]时,各阶模态频率曲线出现一个稳定平台,当t/D在稳定平台区间取值时,模态频率基本不变。考虑薄层单元力学特性,同时为了便于几何建模,选择平台区最小值即薄层单元厚度为3 mm作为后续建模参考。
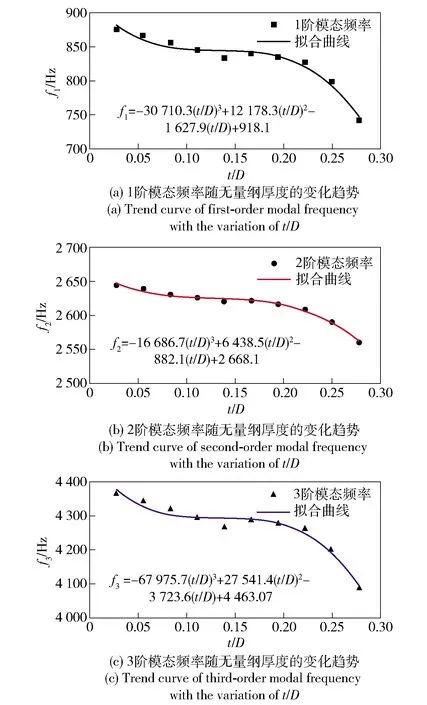
图7 各阶模态频率随薄层单元厚度的变化规律
4.2 薄层单元材料参数研究
螺纹连接薄层单元模型由3个部分组成:内螺纹管、外螺纹管、薄层单元。其中,薄层单元外径为39 mm,内径为33 mm,长度为40 mm.有限元模型如图8所示。内、外螺纹管与薄层单元均进行六面体网格划分,网格单元总数为57 250个。薄层单元表面与内、外螺纹管表面节点进行节点融合处理。
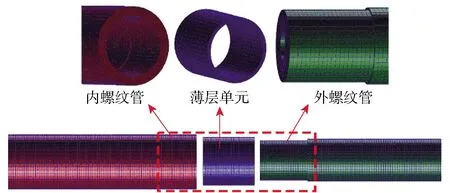
图8 内、外螺纹管与薄层单元有限元模型
在正式计算前,对材料参数与材料模型进行验证,采用Nastran有限元软件对无螺纹试件进行模态分析,材料参数和材料模型与4.1节一致。计算结果如表6所示,前3阶模态频率相比试验值误差分别为1.09%、1.29%、-0.21%,表明材料参数与模型是合理的。
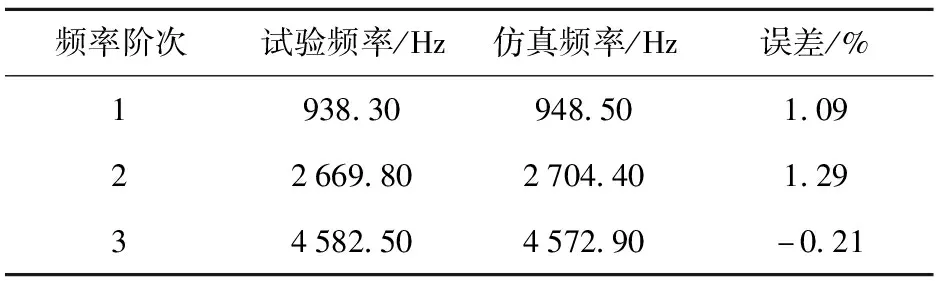
表6 仿真与试验结果对比
为了进一步探索薄层单元材料参数变化对仿真精度的影响,基于薄层单元的弹性模量与剪切模量变化研究模态频率的变化规律。为了便于分析,薄层单元此处采用正交各向异性材料模型进行表征[8]。定义薄层单元的弹性模量与螺纹弹性模量的比值为无量纲弹性模量Es/E,剪切模量与螺纹剪切模量比值为无量纲剪切模量Gs/G.取Es/E=1与Gs/G=1时(无螺纹试件)模态频率f作为基准,对不同Gs或Es下计算得到的模态频率fs进行归一化处理,结果如图9与图10所示。
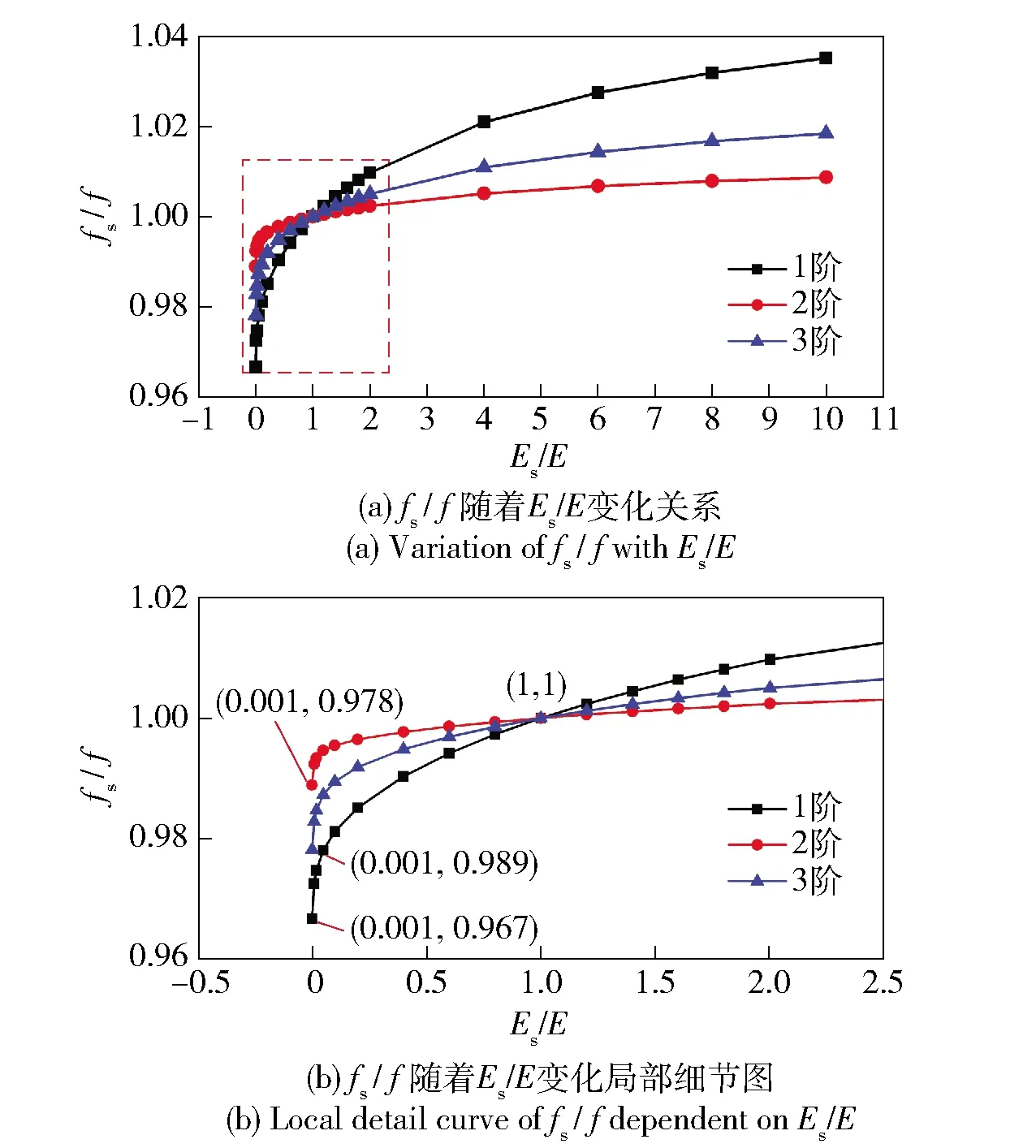
图9 模态频率与无量纲弹性模量变化关系
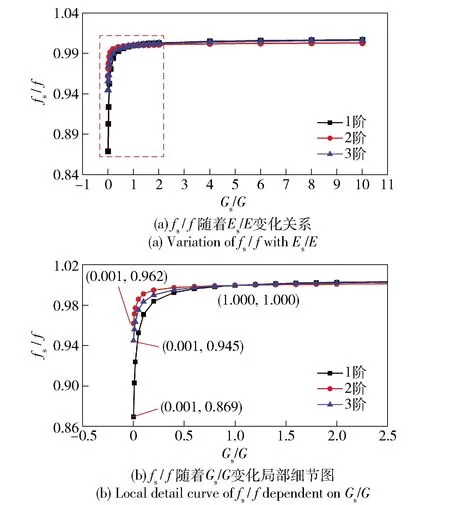
图10 无量纲剪切模量与模态频率变化关系。
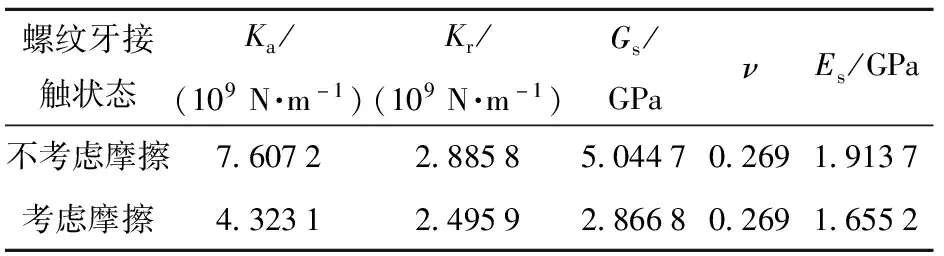
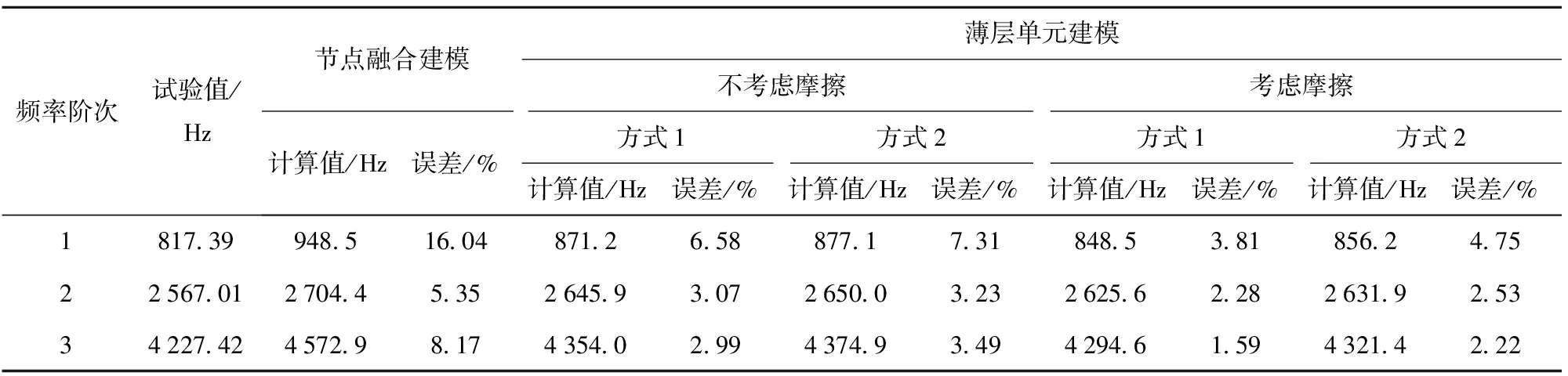
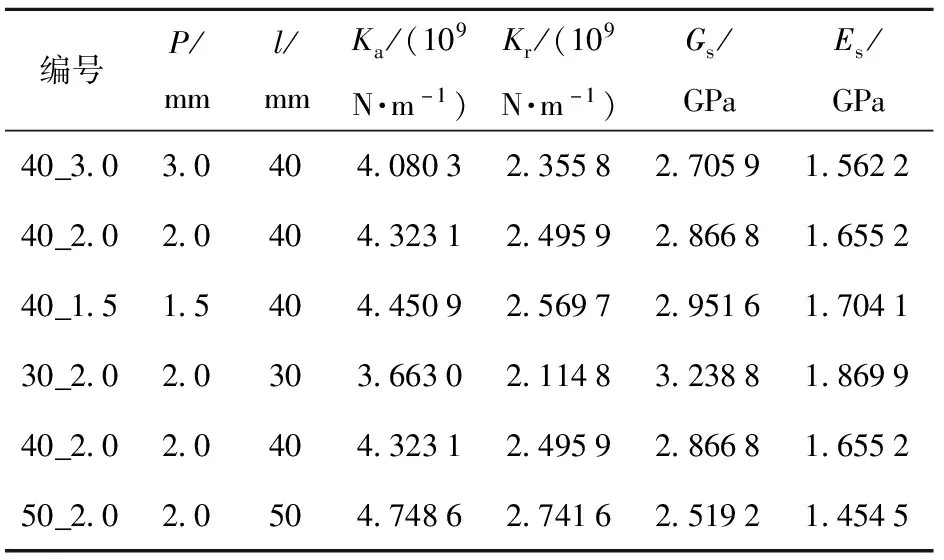
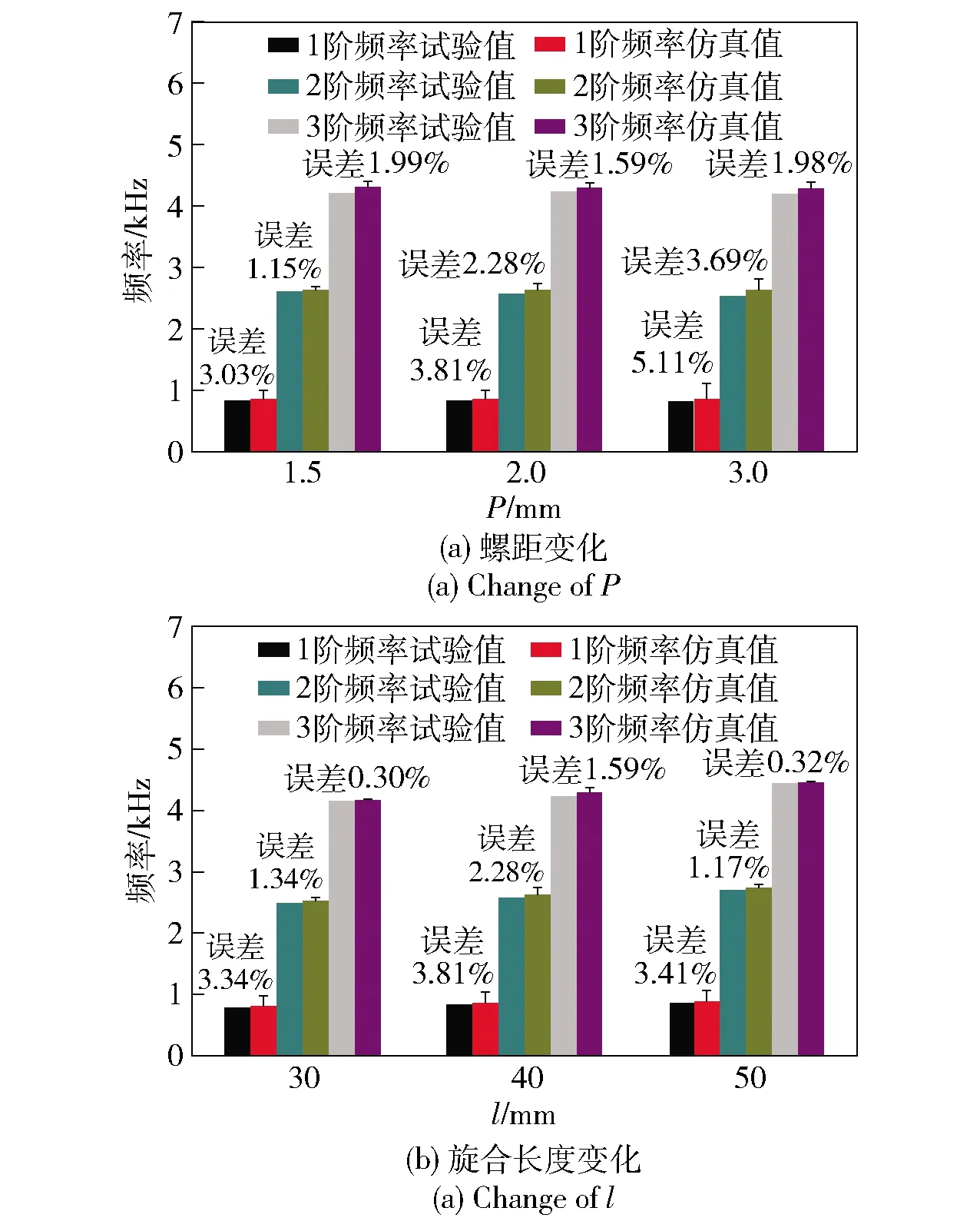
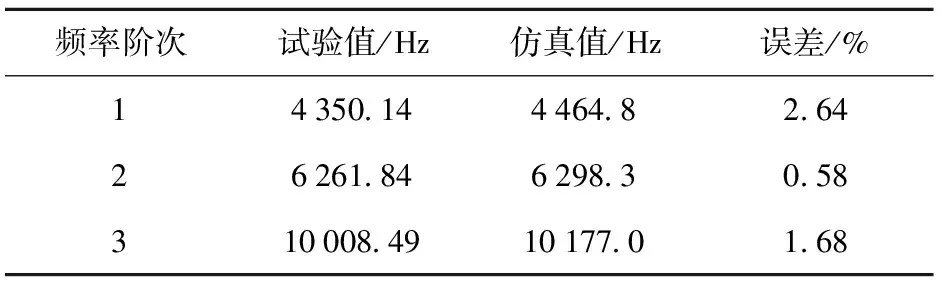
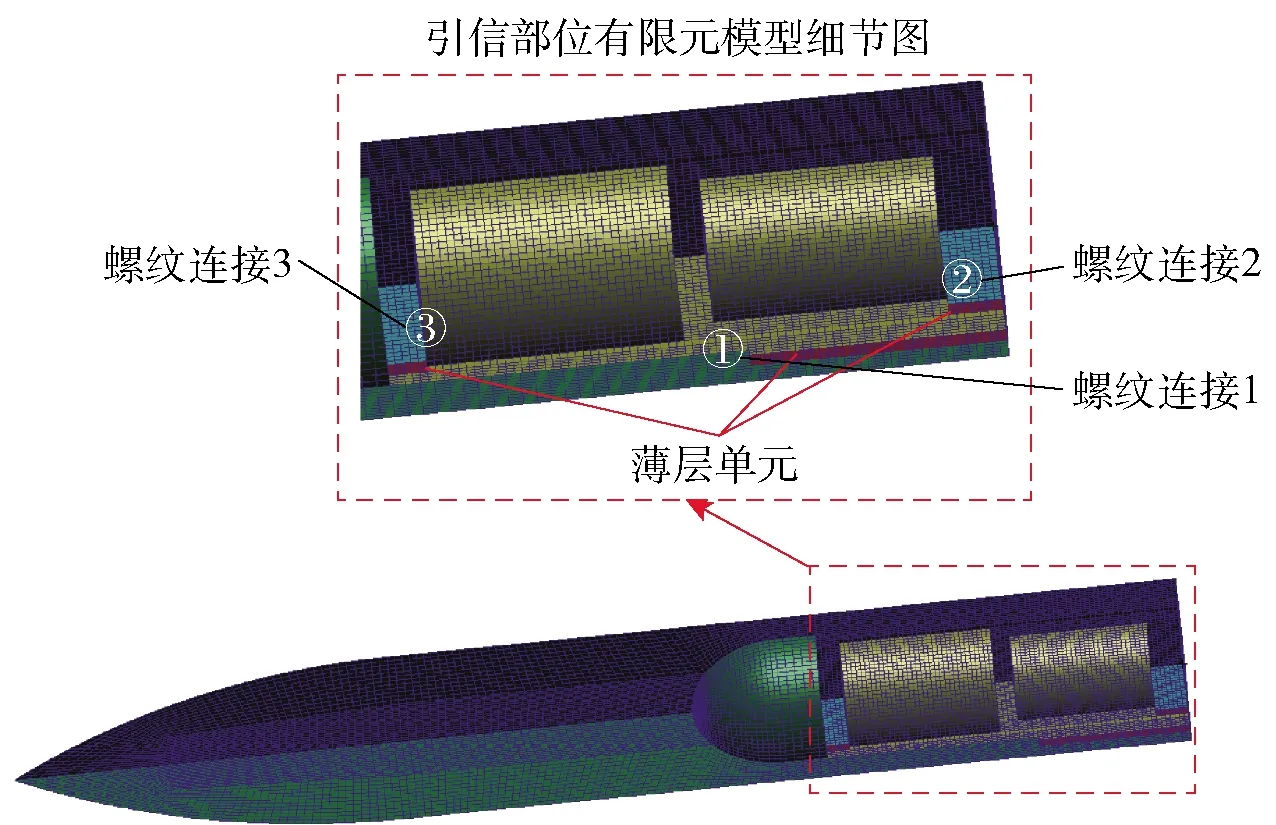
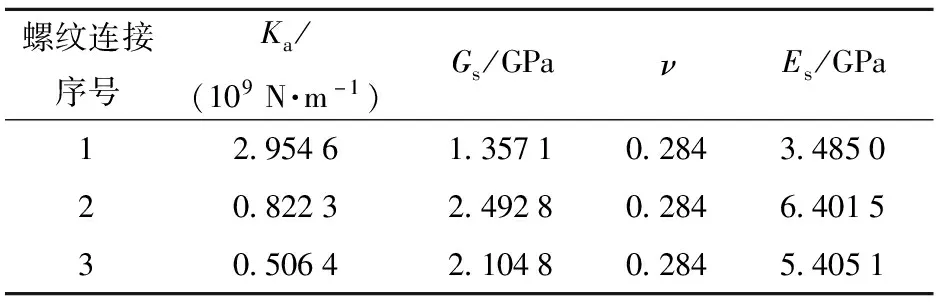
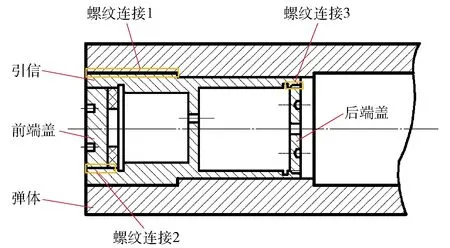
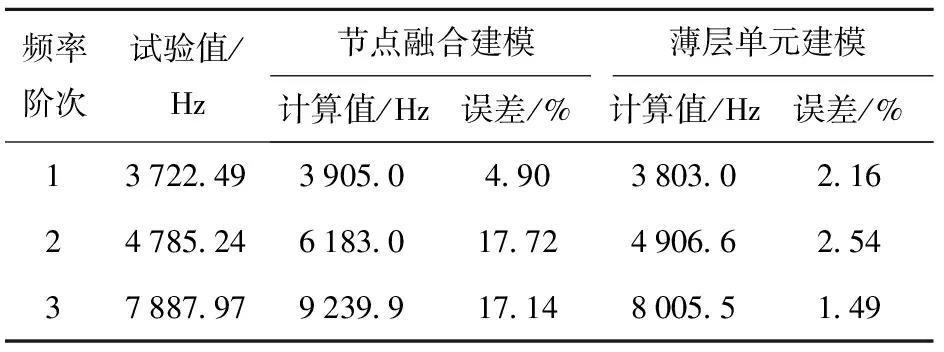
由图9可知:当0 薄层单元弹性模量与剪切模量的取值范围为0 图11 1阶归一化模态频率相对于无量纲剪切模量(或弹性模量)的斜率曲线 针对螺纹接触的处理,现有方法将螺纹接触面处的节点融合,这样的处理方式忽略了螺纹连接之间的接触情况,造成仿真结果误差偏大。采用薄层单元表征螺纹连接之间的接触状态,依据(15)式和(18)式分别在考虑与不考虑螺纹牙接触摩擦力两种情况计算得出薄层单元的材料参数,如表7所示。此外,表7中对薄层单元材料参数考虑两种计算方式:1)分别计算轴向刚度与径向刚度,然后得到Gs与Es,简称方式1;2)首先计算出剪切刚度Gs,然后利用简化计算方式Es=2(1+ν)Gs得到Es,在材料模型中输入Gs与ν即可,简称方式2. 计算结果如表8所示。 表7 薄层单元材料参数 表8 螺纹管模态频率试验结果与仿真结果对比 由表8中计算结果分析可得,与试验值比较,节点融合建模方式得出的前3阶模态频率误差分别为16.04%、5.35%、8.17%,1阶模态频率误差过大的原因可能是激励过程中螺纹出现松动,1阶模态对非线性因素更敏感所致。采用薄层单元进行建模之后,计算精度均有显著的提高,对于不考虑摩擦力的情况,比较两种材料输入方式,方式1计算精度要高,误差分别为6.58%、3.07%、2.99%;考虑摩擦力的情况,方式1计算误差分别为3.81%、2.28%、1.59%.综上所述,考虑螺纹牙之间的接触摩擦获得的薄层单元材料参数更加准确,仿真计算精度更高;同时发现,材料参数计算方式1的计算精度稍好于方式2,但精度差别不大。 在螺纹螺距P、旋合长度l变化时,分别对薄层单元模型的仿真精度进行了研究:1)P变化,l不变(40_3.0、40_2.0、40_1.5);2)l变化,P不变(30_2.0、40_2.0、50_2.0)。所有螺纹的加工精度与配合精度保持不变。考虑摩擦的计算结果更符合实际情况,因此基于考虑螺纹牙摩擦前提下,采用方式1确定薄层单元的材料参数,结果如表9所示。 表9 不同的螺距与旋合长度的螺纹,薄层单元材料参数计算结果 采用薄层单元对各种工况的螺纹进行建模分析,仿真与试验结果对比如图12所示。由图12可知,与试验值比较,薄层单元建模方式误差最大为5.11%,误差最小为0.3%,满足精度要求。综上所述,对于不同P与不同l螺纹连接型号,理论计算获得的薄层单元材料参数均是合理的。 图12 不同工况下薄层单元建模仿真结果与试验结果对比 在开展弹体与引信螺纹连接仿真计算之前,基于弹体(不含引信)有限元模态分析,对仿真材料参数与材料模型进行验证。弹体材料为高强合金钢(30CrMnSiNi2A),E=220 GPa,ν=0.284,ρ=7 800 kg/m3,采用线弹性材料模型进行表征,计算得到前3阶模态频率如表10所示。与试验值相比,1阶、2阶及3阶模态频率计算误差分别为2.64%、0.58%、1.68%,表明材料参数与材料模型是合理的。 表10 弹体模态频率试验结果与仿真计算结果对比 图13为弹体与引信螺纹连接示意图,螺纹连接共3处:1)弹体与引信壳体;2)引信壳体与前端盖;3)引信壳体与后端盖。依据螺纹连接的实际尺寸,在考虑螺纹牙摩擦前提下采用方式2计算薄层单元材料参数,结果如表11所示。引信体材料与弹体选择一致,不考虑引信体材料与弹体不同的情况,选择薄层单元的厚度为3 mm进行建模,在不影响计算精度的前提下对退刀槽、倒角等进行简化处理,弹体与引信系统1/4有限元模型如图14所示,计算中采用全模型进行处理。划分网格时,螺纹连接处网格适当加密,所有网格均采用六面体网格进行划分,网格总数量为245 940个。 图14 弹体与引信系统薄层单元1/4模型 表11 弹体与引信系统薄层单元模型的材料参数 图13 弹体与引信螺纹连接示意图 薄层单元内、外表面与弹体、引信体之间的网格节点进行融合处理。采用MD/Nastran模态分析模块进行求解,最终计算结果如表12所示。由表12可知,相比模态试验结果,节点融合的计算误差分别为4.90%、17.72%、17.14%,采用薄层单元进行建模计算之后,误差下降到2.16%、2.54%、1.49%,表明薄层单元建模方式可以有效地模拟螺纹连接,显著提高仿真计算的精度。 表12 弹体与引信系统模态频率试验结果与仿真结果对比 本文提出用薄层单元来模拟弹体与引信系统螺纹连接,并结合螺纹连接的弹性模型与薄层单元理论,建立了一种薄层单元材料参数的确定方法。通过螺纹管结构和弹体与引信螺纹连接结构模态试验结果对薄层单元模型的准确性进行了验证。得出以下主要结论: 1)基于螺纹弹性模型与薄层单元模型,从理论上建立了一种有效的薄层单元材料参数计算方法,考虑螺纹牙摩擦确定薄层单元材料参数更准确,计算精度更高。 2)薄层单元剪切模量准确确定对仿真计算精度有重要的影响,当无量纲剪切模量取值在(0, 0.2),剪切模量对结果影响占主导,相比弹性模量需优先进行考虑。 3)薄层单元建模方法模拟不同螺距与不同旋合长度的典型螺纹连接结构,最大误差为5.11%,表明薄层单元建模方式可以有效地表征不同状态的螺纹接触状态。 4)将薄层单元建模方式应用于弹体与引信螺纹连接仿真计算中,与传统节点融合的建模方式进行比较,采用薄层单元进行仿真计算后,精度分别由4.9%、17.72%、17.14%提高到2.16%、2.54%、1.49%,表明薄层单元建模方式的有效性,同时也表明本文中所建立薄层单元材料参数确定方式的准确性与合理性。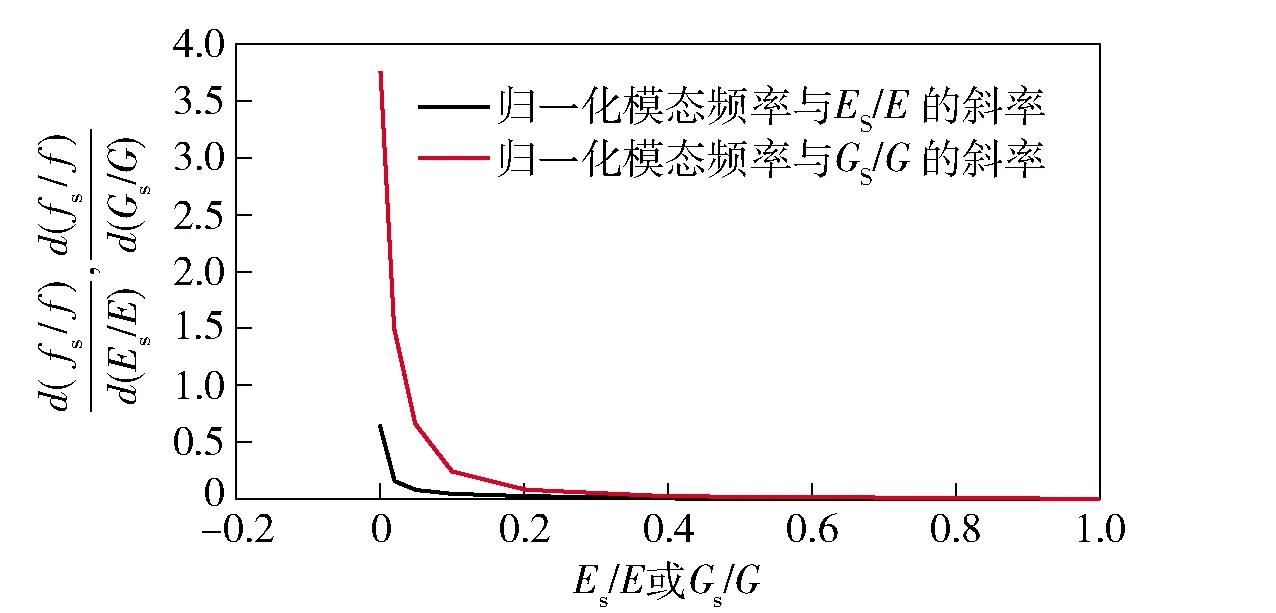
4.3 基于螺纹管薄层单元仿真建模研究
4.4 不同螺距与旋合长度的螺纹薄层单元建模适用性研究
5 基于弹体与引信螺纹连接组合结构薄层单元仿真研究与应用
6 结论

