基于遗传算法优化和模糊控制动态优化的自动变速器换挡规律设计

高子茵，杜明刚，李慎龙，李晋

(中国北方车辆研究所 车辆传动重点实验室, 北京 100072)

0 引言

轻型越野战术车辆作为我国陆军发展装备的核心之一，正在向信息化、高机动等方向发展。车辆换挡规律制定的优劣对整车的动力性、经济性、舒适性等性能带来很大的影响，是车辆变速器控制系统的重要组成部分。

换挡规律的优化研究目前为止已经很成熟，参数的选取由通用的双参数换挡规律过渡到3参数、4参数等[1]，研究方法由传统的理论计算换挡规律改进为智能化换挡规律，主要有模糊控制方法、神经网络方法以及多智能算法融合控制方法[2]。针对越野车辆，晋磊[3]主要针对车辆的动力性能，制定了基于钝化的油门开度、车速和广义道路阻力系数的3参数换挡规律。对于军用履带车辆，一些学者在传统换挡规律基础上进行了优化研究。路红山等[4]在双参数的基础上引入加速度，制定了3参数的换挡规律，考虑了车辆的动态过程。鲁文波[5]设计的多参数多挡位的履带车辆模糊控制算法，更加全面地考虑换挡过程中的一些因素，但同时扩大了控制系统的不稳定性，容易出现一些换挡循环等驾驶员不期望的现象，所以对于参数的选取仍需进一步研究。魏巍等[6]针对液力机械传动履带车辆提出一种换挡点优化的方法，通过运用优化软件iSight进行仿真模型的调用和换挡点的优化，得到优化后的换挡规律，能够有效提升车辆的动力性和平顺性。

综上所述，不同的车辆对于车辆性能的侧重点均不同。本文的研究对象为轻型越野战术车辆，换挡策略为传统的基于车速和油门开度的双参数换挡，通过对换挡点的标定来适应于不同工况。由于轻型战术车辆工作环境复杂多变，对于不同工况的换挡规律要求准则也不相同，而且车辆自动变速存在结构复杂、非线性程度高、控制精度要求高等问题，仅依靠单一的控制方式无法满足控制要求，因此需要集成的智能控制策略来解决复杂的问题，弥补单一控制策略的不足，这也是智能控制研究发展的趋势。

针对上述问题，轻型越野战术车辆主要工作在特殊路面，在工作中要求动力性强，能够快速地投入到作战准备中，换挡策略应该根据车辆所处的复杂环境、运行状态和驾驶员意图进行相应的调整。因此，需要对轻型越野战术车辆当前的换挡规律进行改进和优化。主要应用的方法是改变换挡点以及增加控制参数，具体的技术路线图如图1所示。

图1 技术路线图

1 整车动力系统建模及仿真验证

建立准确的数学模型是研究换挡规律的前提，也是进行验证的理论基础。根据设计要求，利用某战术车的整车参数，如表1所示。

表1 整车参数

运用MATLAB/Simulink软件搭建传动系统的动力学模型。模型主要包括：发动机模块、液压系统模块、机械系统模块、挡位选择模块、整车动力学模块等。整体思路为发动机模块输出扭矩输入机械系统模块，带动行星排旋转，在控制器的作用下，由液压系统模块输出压力作用于机械系统模块内的离合器上，产生相应的构件运动连接关系，最终机械系统的输出轴模块将扭矩传递至整车动力学模型中进行计算，得到车辆的动力学特性。图2为基于变速器的整车多自由度动力学模型。

图2 基于变速器的整车多自由度动力学模型

1.1 发动机模块

发动机作为车辆动力的来源采用查表的方法来获取各个油门开度下的转速转矩值，并综合考虑了泵轮扭矩和负载扭矩对发动机输出扭矩的影响，发动机数学模型为

Te,O=Te-(Tp+Te,l+Ti+Tf)，

(1)

式中：Te,O为发动机输出扭矩(N·m)；Te为在满油门工况时各转速对应的扭矩(N·m)；Tp为变矩器泵轮扭矩(N·m)；Te,l为发动机负载扭矩(N·m)，负载包含1个冷却油泵、1个机油泵和1个燃油泵等，在此模型中当且仅当油门开度为0时作用；Ti在为怠速扭矩(N·m)，仅在发动机转速小于空转限制转速时发挥作用；Tf为摩擦扭矩(N·m)。

1.2 机械系统模块

机械系统模块输入参数为发动机输出转速、离合器各个压力以及变速器输出轴扭矩，输出参数为泵轮转矩、涡轮转速以及变速器输出转速。该模块下主要包括变速器液力变矩器模块、行星变速模块和离合器模块等。

1.2.1 液力变矩器模块

液力变矩器模块根据发动机转速和涡轮转速得到泵轮的转矩以及变矩器工作产生的热流量，并根据液力变矩器原始特性进行建模，数学模型为

(2)

1.2.2 行星变速模块

行星变速模块输入参数为液力变矩器输出的涡轮扭矩参数、离合器压力以及变速器输出扭矩，输出参数为变速器输入轴和输出轴的角速度。具体划分为行星排模块和离合器模块，两个模块连接关系构架如图3所示。图3中：TO为离合器输出轴扭矩(N·m)；ωO为离合器输出轴角速度(rad/s)；θ为离合器输出轴角度(rad)；g(TO)为TO和ωO的函数关系；f(θ,ωO)为θ、ωO与TO的函数关系。

图3 行星变速机构模块建模框架图

1.2.3 离合器与制动器模块

液力变矩器的闭锁离合器以及换挡离合器与制动器工作原理相同，主要包括离心油压计算、离合器扭矩容量计算、离合器滑摩计算和离合器热模块4个部分。该模块的建立同样适用于换挡离合器的模块。

1)离合器油压计算数学模型为

(3)

式中：Fc为离心油压作用在活塞上的作用力(N)；ρo为油液密度(kg/m3)；ω为离合器旋转角速度(rad/s)；do和di分别为活塞外径和内径(m)。

2)离合器扭矩容量计算数学模型为

Tc=FnμffrN，

(4)

式中：Tc为离合器扭矩容量(N·m)；Fn为作用在摩擦片上的压力(N)；μ为摩擦因数，是摩滑速差的函数；ff为摩擦衰减因子，是摩擦副数量的函数；r为摩擦片等效半径(m)；N为摩擦副的数量。

3)离合器传递扭矩计算模型为

(5)

式中：Ts为离合器滑摩扭矩(N·m)；ks为离合器摩滑刚度系数(N·m/(rad/s))；ωs为摩擦片速差(r/min)，

ωs=ωi-ωo，

(6)

ωi、ωo分别为内、外摩擦片的转速(r/min)；T′s为离合器传递扭矩(N·m)。

4)离合器热模型。离合器热模型主要包括离合器温升和油温计算模型。离合器温升计算数学模型为

(7)

热流量计算数学模型为

(8)

1.3 简化传动轴模块

简化输出轴模块输入参数为变速器输出轴转速和车轮转速，输出参数为转矩，作用于车辆动力模块，数学模型为

TS=k(θO-θw)+c(ωO-ωw)，

(9)

式中：TS为传动轴输出扭矩(N·m)；k、c分别为传动轴上的刚度系数(N/m)和阻尼系数(N·m/s)；θO、ωO为输出轴的旋转角度(rad)和角速度(r/min)；θw、ωw分别为车轮的旋转角度(r)和角速度(r/min)。

1.4 车辆阻力模块

车辆阻力模块主要考虑车辆在直线行驶时所受的外力，包括滚动阻力、坡道阻力、空气阻力以及加速阻力，输出的车速作用于挡位选择模块，车辆行驶总阻力为

Ftot=Fr+Fs+Fw+Fa=

(10)

式中：Ftot为车辆总阻力(N)；Fr、Fs、Fw、Fa分别为车辆的滚动阻力、坡道阻力、控制阻力和加速阻力(N)；m为整车质量(kg)；g为重力加速度(m/s2)；f为滚动阻力系数；θs为坡道角度(rad)；ρa为空气密度(kg/m3)；Cd为空气阻力系数；A为车辆迎风面积(m2)；v为车辆行驶速度(km/h)；IF为车辆转动惯量(kg·m2)；Iw、nw分别为车轮的转动惯量(kg·m2)和转速(r/min)；R车轮半径(m)；a为车辆加速度(m/s2)。

1.5 挡位选择模块

挡位选择模块通过不同的离合器闭锁和分离实现6个前进挡以及1个倒退挡，根据闭解锁策略实现液力和机械工况的交替。并且以车速和油门开度作为换挡规律和闭解锁规律的2个参数，具体设计框架图如图4所示。

图4 换挡规律设计框图

本文采用东风康明斯发动机有限公司产ISDe240发动机和美国艾里逊变速箱公司产循环圆直径为310 mm的TC310型液力变矩器，发动机特性参数和变矩器原始特性参数分别如表2和表3所示。

表2 发动机特性参数

表3 液力变矩器原始特性参数

发动机采用全程调速方法得到部分特性曲线，液力变矩器采用原始特性，制定发动机与液力变矩器共同工作的输入输出特性曲线，从而计算液力工况下的换挡点，液力变矩器闭锁后计算机械工况下的换挡点。基于换挡规律主要针对车辆动力性的目标，本文侧重研究动力性换挡规律，具体的设计流程如图5所示。

图5 动力性换挡规律设计流程

通过MATLAB软件的m文件编写计算出基于油门开度和车速的双参数动力性换挡点，如表4所示。引入收敛系数K来定义降挡速差，如(11)式所示：

表4 动力性升挡点

K=(vn,u-vn+1,d)/vn,u，

(11)

式中：vn,u为从n挡升入n+1挡的升挡车速；vn+1,d为一定油门开度时从n+1挡降至n挡的降挡车速。

换挡曲线如图6所示。

图6 动力性升降挡曲线

动力性升降挡点确定之后，用Simulink/Stateflow软件搭建挡位选择模块，采用查表的方法根据不同的车速和油门开度来确定目标挡位。挡位选择模块绘制的流程如图7所示。图7中：gear为挡位；lock为闭解锁状态，1为闭锁，0为解锁；flag为判断标志位。

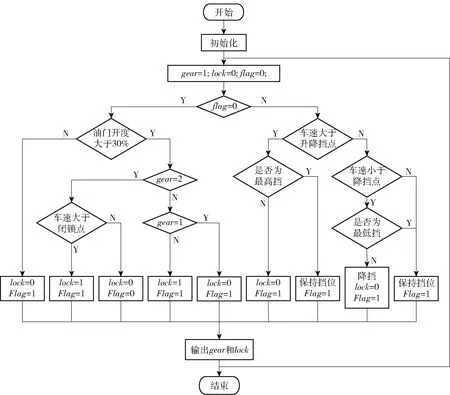
图7 挡位选择模块绘制流程

根据制定的控制策略，以车辆的加速性能为依据进行仿真，得到的车速和挡位如图8所示。

图8 加速性下的车速和挡位

2 遗传算法对换挡规律的优化

在计算理论换挡规律的过程中，采用了大量的近似值，如发动机的转速转矩特性曲线、同一油门开度下相邻两挡车速曲线交点存在误差，通过动力性升降挡曲线可以看出在油门开度变化大的情况下易出现循环换挡现象，导致所求换挡规律在实际应用中并不是最合适的。所以需要对整车的换挡规律进行进一步优化，从而提高车辆的动力性。

2.1 基于遗传算法的换挡点优化问题描述

换挡曲线的制定直接决定了车辆动力性好坏，理论计算出来的换挡点在实车应用中并不是最优结果，为了提升车辆的动力性能需要不断在实车中调试换挡点。根据文献[7-10]了解到遗传算法能够同时优化多个变量，通过制定优化目标能够获得各个油门开度下的最优换挡点。遗传算法的制定流程如图9所示。

图9 遗传算法流程图

依据遗传算法的制定流程，首先进行初始化设置，以各个油门开度下的各挡位升降挡点作为优化变量，目标函数为0～80 km/h的加速时间，如(12)式所示，约束条件为各个换挡点的取值范围：

(12)

式中：ta为加速时间(s)；a1、a2、a3、a4、a5、a6分别为各个挡位的加速度(m/s2)；v1、v2、v3、v4、v5分别为各个挡位的换挡点车速(m/s)。

2.2 遗传算法换挡点优化的实现

遗传算法换挡点优化的实现首先要设定一系列的参数，主要有种群染色体个数、染色体节点数、迭代次数、突变概率以及交叉概率等，参数值设定如表5所示。然后初始化种群，对染色体进行随机赋值，用车速范围将个体限制在规定区间之内。

表5 各个参数设定值

适应度值是评价个体的好坏程度，越大说明个体越好，所以遗传算法要求适应度值非负。但本文的目标函数加速时间需要求最小值，所以将最小的目标根据适应度非负原则转化为求最大值的形式，将适应度函数转化为求解最大的加速度值。转化后的公式如(13)式所示：

(13)

式中：amax为最大加速度(m/s2)。

根据加速度公式：

a=

(14)

式中：Ad和Bd分别为滚动阻力系数与车速函数关系的常数项和一次项；Fb为制动阻力(N)；Ai、Bi、Ci分别为加速度和车速函数关系的二次项系数、一次项系数和常数项。

最终得到适应度函数：

(15)

式中：Ai1、Bi1、Ci1分别为1挡内的加速度和车速函数关系的二次项系数、一次项系数和常数项；Ai2、Bi2、Ci2分别为2挡内的加速度和车速函数关系的二次项系数、一次项系数和常数项；Ai5、Bi5、Ci5分别为5挡内的加速度和车速函数关系的二次项系数、一次项系数和常数项；Ai6、Bi6、Ci6分别为6挡内的加速度和车速函数关系的二次项系数、一次项系数和常数项；

随着染色体的交叉变异，每一代的最大适应度值所对应的染色体均不同，所以输出每一代的最优染色体，从而遵循优胜劣汰的原则，整体迭代流程如图10所示。

图10 遗传算法迭代流程

2.3 仿真验证及结果分析

根据图10中算法流程，利用MATLAB软件的m文件编写程序，为了避免循环换挡现象，10%～50%油门开度时采用基于车速的单参数换挡规律，则优化后各个油门开度的换挡点如图11所示。将优化后的换挡点写进模型挡位选择模块中，进行加速性能仿真验证。表6为100%油门开度下优化前后换挡点，将换挡点作为模型输入，同样采用查表法，对换挡规律优化前后进行加速特性仿真分析，如图12所示。

图12 加速性下优化前后结果对比

表6 100%油门开度下各挡换挡点

图11 优化后的换挡规律曲线

通过分析0～80 km/h的加速时间来验证优化后的换挡规律是否提升车辆的动力性，优化前加速时间为19.12 s，优化后的加速时间为18.35 s，可见，换挡点的优化对车辆的动力性能有所改善。

3 基于模糊控制的动态换挡规律优化

遗传算法修正的换挡规律是基于发动机稳态模型的双参数换挡策略，但文献[11]研究结果表明，发动机在工作中，有66%～80%的时间是处于动态工况的，动态工况下的发动机转速、油门开度、进气管气流运动等参数同时发生变化，会使得发动机的动力性等指标相对于稳态工况发生变化。文献[12]中研究结果表明动态与静态的换挡点速差最大高达13%，显示两参数控制不符合实际，不能保证车辆始终处于最佳挡位行驶，影响整车最佳性能发挥，所以在实车换挡策略制定中，需要考虑实际动态工况。加速度参数能够很好地反映车辆纵向状态以及对发动机转矩有重要影响，所以引入加速度对双参数换挡规律进行优化。轻型越野战术车辆的自动变速系统是极其复杂的非线性系统，而模糊控制理论对数学模型的精确度要求不高，正适应于此系统[13-14]。将模糊控制应用在该轮式车辆上，对换挡规律进行修正，其修正流程如图13所示。

图13 换挡规律模糊修正流程

3.1 模糊控制算法问题概述

模糊控制的整体思路为对精确的控制变量和输出变量进行模糊化处理，制定控制变量与输出变量的变化规则，经过模糊推理，得到输出变量的模糊值，最后进行解模糊处理，得到修正量，输出到被控对象系统中[15-17]。本文模糊控制器的设计步骤如图14所示。

图14 模糊控制基本原理

3.1.1 选择模糊控制器的输入量和输出量

针对变速器换挡系统的特点，采用多输入单输出结构的模糊控制器，以车速、油门开度、加速度作为模糊控制器的输入量，换挡点的修正量为输出量。

3.1.2 论域变化

将车速、油门开度和加速度的实际论域变换到内部论域分别为{0，1，2，3，…，29，30}、{0，1，2，3，4，…，10}、{-3，-2，-1，0，1，2，3}、{-2，-1，0，1，2}。根据车辆的实际行驶情况，各个输入参数的变化范围：车速为[0 km/h,150 km/h]；油门开度为[0,1]；加速度为[-6 m/s2，6 m/s2]；车速变化量为[-10 km/h，10 km/h]。可得车速、油门开度、加速度和车速变化量的量化因子分别为0.2、10、0.5、5.

3.1.3 模糊化

将精确的输入量转化为模糊量。车速v划分为5个模糊集合，包括大(VB)、大(B)、中(M)、小(S)、极小(VS)，确定模糊子集为{VS S M B VB}。油门开度划分为5个模糊集合，包括大(VB)、中大(MB)、中(M)、中小(MS)、小(VS)，确定模糊子集为{VS MS M MB VB}。加速度划分为7个模糊集合，包括正大(ZB)、正中(ZM)、正小(ZS)、零(Z)、负小(FS)、负中(FM)、负大(FB)，确定模糊子集为{FB FM FS Z ZS ZM ZB}。输出换挡点修正量划分为7个模糊集合，包括正大(PB)、正中(PM)、正小(PS)、零(Z)、负大(NB)、负中(NM)、负小(NS)，确定模糊子集为{NB NS NZ Z PZ PS PB}。

3.1.4 模糊量的隶属函数

隶属函数必须覆盖整个取值范围，一般情况下，是在整个范围内均匀分布，密级程度根据参数是否敏感，若敏感可以取得密集一些。并且，隶属度函数之间应该有重叠区域，通常为20%～55%，来提高鲁棒性。MATLAB软件中内嵌的模糊控制器隶属度函数有三角型、梯型和正态分布型等。为了使结果更加符合实际情况，输入变量的隶属度函数都采用正态分布型；同时对于输出参数，采用梯形方式，有利于输出值的判别，图15为车速、油门开度、加速度以及输出换挡点修正的隶属度函数曲线。

图15 各个参数模糊集隶属度函数曲线

3.1.5 模糊控制规则。

本文采用的是3输入变量和1输出变量，3个输入变量分别赋予了5、5、7个语言值，采用Madani推理法，依据输入参数模糊集合数，得到控制规则数共5×5×7=175条。以提升动力性为目标确定输入输出参数之间的关系，以加速度为参考依据：加速度绝对值越大，换挡点修正量也越大。若加速度为正时,此时驾驶员意图为增速，修正量为负，有利于快速升到高挡；加速度为负时，驾驶员意图为减速，修正量为正，有利于车辆快速降到低挡位。

按照以上输入输出的关系，制定模糊规则。以车速VS集合为例，得到加速度、油门开度和换挡点修正量的模糊推理表，如表7所示。

表7 车速集合为VS时的模糊推理表

3.1.6 去模糊化

根据制定的模糊规则，采用重心法进行去模糊化，得到仿真平台可以识别的精确换挡点。图16为加速度、油门开度与修正量的关系曲面，图17为加速度、车速与修正量的关系曲面。

图16 加速度、油门开度和修正量的关系曲面

图17 加速度、车速与修正量的关系曲面

3.2 仿真验证及结果分析

将模糊控制器模块引入换挡选择模块，对换挡点进行修正，验证车辆的加速性能，将遗传算法优化后换挡规律以及经过模糊控制修正后换挡规律的仿真结果进行分析对比，如图18所示。

图18 加速性下优化前后车速对比

综上3种方法对0～80 km/h的加速时间进行分析，理论计算换挡规律0～80 km/h的加速时间为19.12 s，通过遗传算法优化后的换挡规律加速时间降低到18.35 s，再通过模糊控制器的修正后加速时间为15.38 s.加速时间减少了19.56%，动力性得到明显提升。

4 换挡规律实车验证

4.1 实车试验平台

基于轻型越野战术车辆的装车试验平台，对设计的换挡规律进行实车验证。将设计的换挡规律编写成实车可识别的C语言代码，通过CAN总线接口进行动力传动状态信息实时采集存储，包括发动机转速、发动机转矩、油门开度、变速器输出轴转速和挡位等一系列参数，为后续数据处理和分析提供依据。

4.2 换挡规律的实车验证

将理论计算换挡规律、遗传算法优化后换挡规律以及经过模糊控制修正后换挡规律分别通过实车验证，驾驶员通过给定100%油门开度来进行试验。分析处理得到的各组数据，将3组车速和挡位进行分析对比，如图19所示。

图19 100%油门开度下优化前后结果对比图

综上3种方法得到0～60 km/h、0～70 km/h、0～80 km/h的加速时间，如表8所示。

表8 加速时间对比

由图19和表8可以看出：优化后加速时间明显减少。以0～80 km/h加速时间为例，理论计算换挡规律所用时间为18.96 s，利用遗传算法对换挡点优化后加速时间减少为16.84 s；之后引入加速度参数制定3参数的模糊控制器，将加速时间缩短到15.08 s，0～80 km/h的加速时间减少了20.46%，车辆的加速性能明显提高。

以3种换挡规律100%油门开度下行驶到80 km/h这一时间段的挡位信息和发动机转速转矩信息为依据，分别绘制发动机转速转矩散点图和挡位占比柱状图，如图20～图22所示。

图20 原始换挡规律实车使用工况

图21 遗传算法优化换挡规律实车使用工况

图22 模糊修正换挡规律实车使用工况

根据发动机的实际使用工况，可以明显看出转速转矩点越来越趋向于大功率范围，说明模糊控制修正后换挡规律有助于提升车辆的动力性。根据各个挡位占比图可以看出：在各种换挡规律下，0～80 km/h加速工况下1～3挡所占时间也不同。在理论计算换挡规律下，工作在1～3挡的时间百分比为52.61%；遗传算法优化后换挡规律下，工作在1～3挡的时间百分比为61.14%；模糊控制修正后换挡规律下，工作在1～3挡的时间百分比为64.1%.由此可以看出，模糊控制修正后换挡规律可有效提升低挡位工作时间比例，进而提升整车的加速性能。

5 结论

以轻型越野战术车辆为研究背景，通过数学模型分析、仿真模型搭建以及试验验证等方法研究不同的换挡规律对车辆的动力性的影响。得出以下主要结论：

1)基于理论计算得到的双参数换挡规律在实际应用中误差较大的特点，采用遗传算法对换挡点进行优化研究，通过仿真模型验证修正后0～80 km/h的加速时间有效减少了4.03%，动力性得到改善。

2)引入加速度参数对换挡规律进行动态优化，制定了3参数的模糊控制器，通过仿真模型验证优化后0～80 km/h的加速时间有效减少了19.56%，动力性得到了明显提升。

3)基于轻型越野战术车辆的装车试验平台进行换挡规律优化前后的实车验证，分别从0～60 km/h、0～70 km/h、0～80 km/h的加速时间、发动机使用工况和各个挡位占比三方面进行试验数据分析，得到优化后的换挡规律明显提升了车辆的动力性能，达到了本研究目的。