真教真学:公开课应当追求的教研品质
——以“不等式的解集”公开课为例
王小林 (江苏省苏州工业园区东延路实验学校 215021)
1 从一节“不等式的解集”公开课说起
最近,笔者在“一师一优课”晒课平台上观摩学习了一节公开课“不等式的解集”,该课教学流畅、设计精致,教师有问学生即齐答,一顺到底,把一节数学新授课上成了班团活动课,表演的成份多了一点,真教、真学的味道淡了一点.以下先概述该课教学流程与观课所见,再跟进评课意见.
教学活动1 复习旧知
教师结合PPT上呈现并提问:数轴的三要素是什么?数轴上的点所表示的数有什么大小特点?什么叫不等式的解?方程x+2=5的解是什么?不等式x+2>5,x=3是它的解吗?x=4呢?x=5.5呢?你们还能举出这个不等式的其他解吗?
观课记录与随感:教师提问旧知,目的是引出新知,是有积极意义的,学生多是齐答,符合学情.
教学活动2 引出新知
教师:从不等式x+2>5有很多解来看,我们是列举不尽的,但它们可以组成一个集合,称为不等式x+2>5的——(学生齐答“解集”).
接着教师板书课题“不等式的解集”,但没有板书它的概念.然后结合PPT演示不等式的解集在数轴上的直观表示方法(图1,图2).
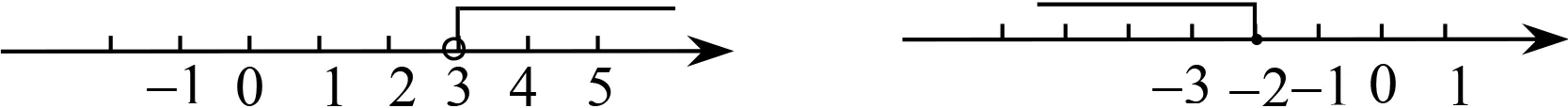
图1 图2
组织学生讨论表示解集的折线所指方向有什么不同?它们有什么规律?数轴上空心圆圈与实心圆点的意义是什么?(教师每问一句,学生多是立即齐答,而且都是正确的)比如根据不等号的类型,大于向右画,小于向左画,还有空心圈与实心点的区别.
观课记录与随感:这个环节是新授内容,学生如果没有提前预习或学习,是不可能教师一问学生立即齐答的.从这个环节开始,这节课就有点“变了味”,让人怀疑这不是一节新授课,而是一节复习课.
教学活动3 运用新知
教师借助PPT分别出示了6组习题,其中第1组是判断题(共8个小题),分别让学生辨析方程的解、不等式的解与解集这些概念;第2组题是选了5个不等式的解集,让学生在数轴上表示出来,其中最后一个解集是-3 图3 图4 图5 观课记录与随感:第5题教师准备了PPT进行动画演示,直接讲评并与学生核对答案;第6题在新授课中出现是很有挑战的,但是学生直接就说出答案,教师可能也觉得这是本课的难点,先肯定了学生的答案,然后借助于电脑上准备好的动画来演示,解释为何是3 教学活动4 课堂小结 教师准备了小结问题:这节课你学了哪些内容?你有何收获或感受?还有哪些需要老师和同学们帮助你解决的问题吗?你还有什么新的见解? 观课记录与随感:学生在这些小结问题的引领下进行小结发言后,教师布置作业,然后下课,时间也正好.这是一节非常“精致”的公开课,在这节晒课的网页下面的“跟帖”中一片“点赞”“叫好”.然而笔者总感觉缺了一点什么?那就是少了一些真教与真学的味道. 上文关注的公开课是一节数学新授课,从观课所见,可以确定的是学生课前进行过充分的预习,新授课中表演成份太多,真教、真学的味道偏淡了,以下再围绕新授课如何真教真学,提出一些思考. (1)很多数学新授课不宜让学生提前预习 很多数学概念或性质在引入时,需要学生有一定的陌生感,而不是提前预习后“被剧透”.比如勾股定理、三角形中位线性质、一元二次方程的根与系数关系、函数图象,等等,这些数学知识如果学生提前预习,则教师所设定的数学情境往往会失效.因为学生已知晓本课要学习的主要内容,失去了这些情境驱动下的探究、发现的味道,不利于培养学生发现和研究新数学对象的能力,抽象、建模、推理等数学核心素养的培养也就成了一句空话. 以上文关注的新授课为例,这节课内容简单,根本不必提前让学生预习.当开课阶段从方程的解引出不等式的“很多解”之后,教师可以在板书(图6)上渐次写出“不等式x+2>5的解x=4,x=5.5,x=11,…”我们把这些符合不等式“x+2>5”的所有解组成的集合简称该不等式的“解集”. 图6 这样的概念不需要学生提前预习,课堂上教师进行形象生动的讲解、归纳、概括,引入新知,有利于学生将来自己研究、归纳和概括一个新的数学对象. (2)数学新授课中的概念、性质需要板书 章建跃博士曾指出一些数学新授课存在“一个定义,三项注意,大量练习”的现象.这种教学现象主要表现为数学概念出现太快,缺少必要的情境创设以及去情境化的抽象过程,然后就是误以为新概念太简单,不值得、不需要板书,只要写出关键词,然后梳理几个注意事项,这些注意事项更多是针对接下来要讲解的练习服务的.我们认为:当一个新的数学概念引出之后,不要急于推出练习或小结注意事项,而应该在黑板上书写出这个概念的完整内容.比如不等式的解集经过上面图6的归纳之后,还应该在主板区书写“不等式的解集:一个含有未知数的不等式的所有的解,组成这个不等式的解集.”接着指出“解不等式:求不等式的解集的过程,叫做解不等式.”事实上,新授课教学时,板书新知虽然会用去一些教学时间,但这些时间可以成为更多学生理解新知识的必要时间,因为多数学生接受一个新知识是需要内化、理解的时间的,不能用PPT一闪而过,误以为学生都能像拍照片一样将新知全部存储在大脑中. (3)数学新授课习题训练要注意内容效度 我国著名教育心理学家林崇德先生曾指出,发展学生的思维关键是训练学生的概括能力.数学新授课的教学重点应在知识生成、归纳与概括上,而不是像复习课那样“过电影”.这就要求我们不能被“一个定义、三项注意、大量练习”挤占新知生成的教学时间.以上文课例来说,所选题组太多,达到6个,而且有些题组所含小题量也偏大,而且第6题已明显超出新授课的教学要求,拔高、超标要求,让一些教辅资料上的拓展热点习题提前进入了新授课的课堂.这里,涉及新授课选题的内容效度的问题,所谓内容效度,就是围绕课时教学目标选题时,要想清入选的例习题的训练重点是否贴近教学目标、训练主线,而不是难点集中在分类讨论、构图分析等非本课时重点内容上.我们见到很多新授课在选编例习题时,喜欢增设一个“链接中考”的教学环节,这种应试教学的追求让学生学习全程都在“备考”,增加了紧张、功利的氛围,而且有些中考试题的考查目标是针对整个初中学段而设计的,简单地把一些中考题、地区期末考题、中考模考题“链接”在新授课中是不合适的,往往会出现内容效度不高的问题. 各级教研活动都会开设示范课、公开课、研讨课,承担这些上课任务的教师都会精心准备、反复打磨,以便在这些公开课上精彩亮相,所以很多公开课往往比常态课更加精致,特别是学生在学习或练习过程中一些出错现象会被掩盖,使得课堂教学失真.想来,追求真教、真学也应该是公开课教学活动中“真研”的一种表征吧.


2 公开课应追求真教真学的教研品质
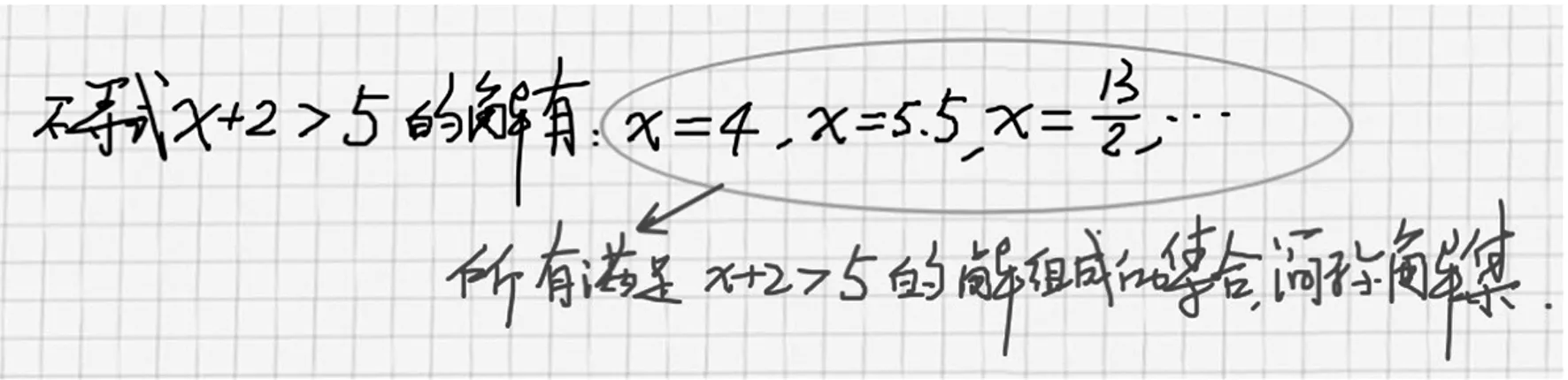
3 结束语

