考虑曲面接触斑的轮轨滚动接触行为分析

陈 雨，王攀杰，孙耀亮，安博洋，张 岷，王 平

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.中铁第一勘察设计院集团有限公司，陕西 西安 710043)

由于铁路运营速度的提高和轴重的增加，轮轨接触条件恶化，轮轨间磨耗加剧，这不仅会增加运营成本，甚至还会危及行车安全。国内外学者针对轮轨磨耗进行了大量理论与试验研究，轮轨滚动接触模型作为其中重要的一环被应用于轮轨磨耗仿真分析中。杨光等[1]采用Hertz接触理论结合Fastsim算法研究了高速列车曲线通过时的轮轨磨耗情况；王璞等[2]研究了重载线路不同地段钢轨磨耗的发展规律；安博洋等[3]采用基于虚拟渗透的非Hertz接触简化算法分别结合Fastsim和FaStrip预测了接触斑内轮轨磨耗深度的分布；李霞等[4]采用Kalker三维非赫兹接触模型预测了朔黄重载线路曲线部分的钢轨磨耗，并与实测结果对比发现基本吻合，但是高轨的轨距角部分磨耗相差较大；孙宇等[5]采用Kalker三维非赫兹接触模型预测钢轨沿纵向和横向磨耗的演变形态。以上均是对区间线路的分析，道岔区的接触更加复杂。徐井芒等[6]采用半Hertz接触算法结合FaStrip分析了轨道参数对道岔区钢轨磨耗的影响；马晓川等[7]对比分析了不同非赫兹滚动接触算法求解道岔区滚动接触行为时的计算精度和效率，建议道岔区采用Schani模型。

目前用于轮轨接触分析的模型大都基于平面假设，但当车辆经过道岔或者小半径曲线地段时，磨耗的轮缘与轨距角易发生共形接触，此时的接触斑是曲面形式，因此需要考虑更精确的模型计算轮轨接触力，进而分析轮轨磨耗和疲劳损伤等问题。

基于计算机和有限元模型的发展，不少学者利用有限元方法计算轮缘与轨距角发生共形接触时的接触应力。金学松等[8]基于Kalker的三维弹性体非赫兹滚动接触理论，考虑曲面接触斑，利用有限元法推导力与位移之间的关系，建立了任意曲面接触斑状态下的接触余能表达式；李自力[9]利用有限元法计算准四分之一空间的影响因子，替代Kalker三维滚动接触理论中的基于平面半空间假设的影响因子，可求解轮缘与轨距角的共形接触问题；竺春海等[10]采用有限元参数二次规划法求解轮轨共形接触问题，得到了轮缘贴靠钢轨轨距角的过程中接触力的变化规律；Edwin等[11]基于李自力的研究，利用有限元得到轮缘与轨距角发生共形接触时的影响因子，并与CONTACT数值程序结合，研究了共形接触程度对接触应力分布的影响；杨新文等[12]利用有限元法计算轮轨法向接触影响系数，对Kalker的三维非赫兹滚动接触理论中的法向应力计算部分进行修正，研究了重载铁路曲线超高对钢轨磨耗的影响。以上研究均利用有限元法得到轮轨间的影响因子进而分析共形接触问题，虽然提高了精度，但计算效率低，不适合大规模的计算。Blanco等[13]在Bossinesq-Cerruti半空间影响因子的基础上进行了修改，提出了一种求解任意空间影响因子的近似方法，并与有限元方法得到的影响因子进行对比，结果基本吻合且效率得到了极大的提高；许玉德等[14]参考Blanco提出的影响因子，提出了最小余能方程中影响系数的修正公式，用于求解非平面接触应力。

现有文献中未详细对比分析基于平面假设的CONTACT数值程序与曲面算法的差异性，未指出在轮缘与轨距角发生共形接触时，采用曲面算法的必要性。本文基于Kalker的三维非赫兹弹性体滚动接触理论(又称“精确理论”)对其中的法向间隙、刚性蠕滑率和影响因子进行修正，使其可考虑轮轨间曲面接触斑，并对比分析了曲面算法和CONTACT在不同接触情况下计算得到的接触面积和接触应力等，研究了2种算法的一致性和差异性。本文的计算分析可为轮轨磨耗和疲劳损伤研究选择适当的轮轨滚动接触模型提供参考。

1 考虑曲面接触斑的轮轨滚动接触算法

车辆运行过程中，会遇到小半径曲线，这种地段轮缘与轨距角磨损通常较为严重，可能发生“共形接触”。这种情况下，基于平面假设的Kalker精确理论只能得到近似解，基于此，本文对CONTACT的输入参数进行修改，使其适合求解共形接触这种曲面形式的接触斑问题。

1.1 基于平面假设的Kalker精确理论

Kalker精确理论通过将轮轨的潜在接触区域离散化，基于弹性半空间假设，利用Boussinesq-Cerruti公式，得到三维弹性体非赫兹滚动接触最小余能的表达式[15-16]为

(1)

式中：AC为接触斑区域；h为两接触体未变形前的法向间隙；δp为渗透量；un和uτ为接触体在法向和切向的弹性位移差；pn和pτ为相应方向的接触应力；u′τ表示前一时刻的切向弹性位移差；g=μpn为切向接触边界，μ为恒定摩擦系数；Wτ为切向刚性滑动量；dx为接触斑单元的纵向宽度；dy为接触斑单元的横向宽度。

弹性变形差u可以通过Boussinesq-Cerruti的力-位移方程求解

(2)

式中：上标(1)、(2)分别为车轮和钢轨；AIiJj为影响因子，表示当单元J承受沿j方向的单位荷载时单元I处产生的沿i方向的弹性位移；AInJn为单元J承受沿法向的单位力时单元I处产生的沿法向的弹性位移；AIτJτ单元J承受沿切向的单位力时单元I产生的沿切向的弹性位移；Bij为j方向单位力引起车轮和钢轨沿i方向的弹性位移差，其具体表达式可参考文献[15]。

由于Kalker精确理论基于平面假设，适用于求解平面形式的接触斑[16]，本文为了叙述方便，将其简称为“平面算法”。

1.2 曲面算法

曲面算法与平面算法的主要区别在于考虑其接触斑为曲面，接触斑内沿横向分布的各点与接触点的法向不再相同，这会影响接触斑内未变形前的法向间隙、刚性蠕滑率和影响因子的计算，而这些是计算轮轨法向和切向应力的基本输入参量，因此本文主要对CONTACT的这3个参量进行修改。

1.2.1 法向间隙

轮轨潜在接触区域的法向间隙是计算轮轨法向接触问题的基本几何输入变量。首先定义全局坐标系OXYZ，原点O位于无位移时的轮对质心处，X轴指向轮对前进方向，Z轴垂直于轨道平面向上，Y轴水平向右，全局坐标系固定不变。平面算法的接触点坐标系为Ocxyz，原点Oc位于轮轨接触点，x轴指向车轮前进方向，y轴指向Oc处的切线方向，z轴指向Oc处法线方向，接触斑内沿横向y轴各点法向与接触点的法向z一致；曲面算法的接触点坐标系为Ocxsn，x轴指向车轮前进方向，s轴指向曲面接触斑横向，n轴指向接触斑各点局部坐标系法向，接触斑沿横向各点法向随接触面的几何发生变化，见图1。

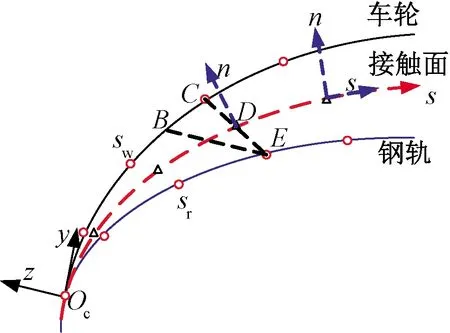
图1 2种算法的法向间隙示意图

轮轨接触斑内质点对产生接触的条件是接触质点对到接触点的弧长相等。以接触斑内E点为例说明2种算法计算法向间隙的区别，见图1，BE与接触点处法向Ocz平行，平面算法中考虑BE段的距离即为轮轨间法向间隙，这在接触点附近轮轨曲率半径很大时可以满足；但是在轮缘与轨距角形成曲面接触的情况下，BOc与EOc距离并不相等，即此时B、E并未产生接触，因此平面算法会高估真实的法向间隙。

曲面算法求解法向间隙的思想在文献[11，13]中有提及，但是未给出数学表达式，本文采用一种近似方法。根据切平面坐标系Ocxyz和曲面坐标系Ocxsn可建立起(y，z，s)之间的对应关系，OcE和OcC弧长坐标sw和sr相等，那么接触斑内D点对应的法向间隙ds为

(3)

式中：θ为EC间距离与D点的局部法向n间的夹角。

分别采用平面算法和曲面算法得到轮轨二维法向间隙f(y)后，假设沿纵向x方向仍遵循Hertz椭圆分布，可得三维的法向间隙

h=Ax2+f(y)

(4)

式中：x为接触斑内纵坐标；A=1/(2R)，平面接触算法中R=R0恒为接触点的滚动圆半径，曲面接触算法中R是接触曲面沿s轴各点的滚动圆半径。

1.2.2 刚性蠕滑率

轮轨潜在接触区域内的刚性蠕滑率是产生轮轨切应力的主要因素。根据蠕滑率定义，刚性蠕滑率为

式中：wY为车轮绕Y轴旋转的角速度；δ为接触斑各点的接触角，见图2；v0为轮轨接触界面的平均速度，钢轨静止不动，可假设v0=wYR0；εx,εy分别为接触点处的纵、横向蠕滑率。

图2 局部坐标系

参考文献[9]，基于平面假设，接触斑内各点接触角恒等于接触点处接触角，则R0-R=ysinδ0，xsinδ=xsinδ0，平面算法的刚性滑移率为

(7)

曲面算法中，由于接触斑是曲面，接触角并不恒等于δ0，因此各点的刚性蠕滑率为

(8)

在曲面接触算法中，取接触斑内沿横向各点的接触角δ=δ0时，则可得到平面算法刚性蠕滑率公式。

1.2.3 弹性位移差

轮轨潜在接触区域内的影响因子是求解法向和切向接触问题的基本输入参量。在以往的研究[9,11]中，通常采用有限元方法获得任意曲面空间下的弹性位移差，但这会显著地增加计算成本，难以应用于工程计算。为了提高计算效率，本文采用Blanco等[13]提出的可考虑任意曲面的弹性位移差计算方法(该方法的有效性已通过与有限元方法的对比得到了验证)。曲面接触算法求解弹性位移差的示意图图3，α为接触斑内I点与J点的切向角之差。在平面算法中，接触斑内各点的法向与接触点的法向一致，α=0；在曲面算法中，考虑整个接触斑内法向沿接触曲面不断变化，α≠0。

图3 曲面算法弹性位移差的示意

曲面接触的弹性位移差为

(9)

式中：Bij、Bij_c分别为平面算法、曲面算法的弹性位移差，其中,i,j分别为切平面坐标系中的x、y、z方向、曲面坐标系中的x、s、n方向。在平面算法中，对于同种材料，法向与切向互不影响，即Byn、Bxn、Bnx、Bny均为0；在曲面算法中，考虑了法向与切向的耦合。

2 考虑曲面接触斑的轮轨接触行为分析

为了对比平面算法与曲面算法研究轮轨接触行为的不同，本文以中国S1002CN车轮踏面和CHN60钢轨型面为例进行计算。车轮名义滚动圆半径为460 mm，轨距为1 435 mm，轨底坡为1/40。轮轨接触特性的计算参数：轮轨垂向力为83.3 kN，轮轨摩擦系数为0.3，泊松比为0.28，剪切模量为82 GPa。轮轨间接触位置大致可以分为3种：车轮踏面与轨顶接触、车轮轮缘与轨距角共形接触和车轮轮缘与轨距角凸面接触，本文主要选取了3个不同的轮对横移量，分别为-6、7.77、9.5 mm代表这3种接触位置。下面主要对这3种典型的轮轨接触情况进行详细分析。

2.1 轮轨法向接触行为分析

分别采用平面算法和曲面算法研究轮轨法向接触行为，计算内容包括轮轨法向间隙、接触斑面积以及法向接触应力分布。

2.1.1 轮轨法向间隙分布

轮轨间的法向间隙会直接影响到接触斑面积和接触应力，分别采用平面算法和曲面算法计算3种接触情况下的轮轨法向间隙，得到的结果见图4，左图为轮轨接触点在全局坐标系下的位置，右图为轮轨法向间隙在接触点坐标系下沿横向的分布。由图4可见，当轮对横移量为-6 mm时，车轮踏面与轨顶接触，轮轨型面在接触点附近的曲率半径与接触斑几何尺寸相比很大，2种算法得到的法向间隙几乎没有差异；当轮轨横移量为7.77 mm时，轮缘与轨距角发生共形接触，轮轨在接触点附近曲率半径均较小且曲率中心在同侧，这种情况下平面算法得到的法向间隙明显比曲面算法大。这是由于曲面算法考虑轮轨接触斑的真实法向，而平面算法考虑接触斑内法向均与接触点处的法向相同；在轮缘与轨距角发生共形接触时，接触斑内法向差异较大，因此平面算法会高估其真实的法向间隙；当轮对横移量为9.5 mm时，轮缘与轨距角发生凸面接触，这种情况虽然轮轨型面在接触点附近曲率半径小且接近，但是曲率中心不在同一侧，可以将轮轨接触面近似看成平面，2种算法得到的法向间隙也几乎没有差异。

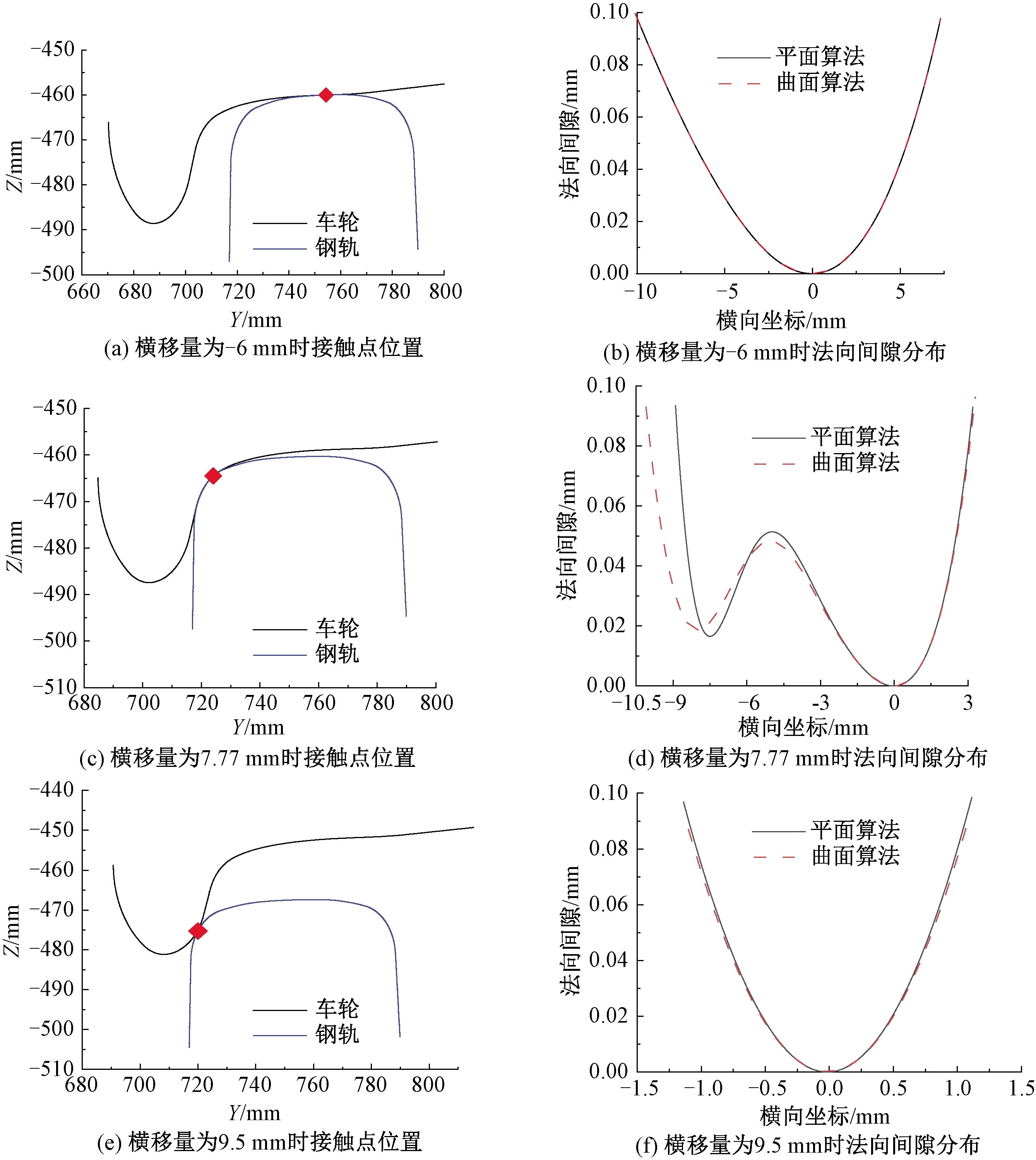
图4 不同横移量下的轮轨接触点位置和接触点坐标系中法向间隙沿横向分布

2.1.2 轮轨接触斑面积和法向应力分布

由于轮对横移量为7.77 mm时2种算法在接触点坐标系内得到的法向间隙差别很大，因此本节分别采用平面算法和曲面算法进一步计算这种接触情况下的接触斑和法向应力分布，结果见图5。由图5(a)可知，曲面算法得到的左接触斑面积明显大于平面算法，其接触斑面积约为84 mm2，平面算法约为76 mm2，比曲面算法的结果小9.5%。原因是平面算法得到的法向间隙更大，因此在相同的法向力作用下其接触面积更小。由图5(b)可见，左接触斑内，曲面算法得到的最大法向应力约为1 732 MPa，平面算法约为2 328 MPa，比曲面算法的结果大34.4%。说明当轮缘与轨距角发生共形接触时，平面算法会高估真实情况下的法向应力。

图5 横移量为7.77 mm时在接触点坐标系下的接触斑和法向应力

2.2 轮轨切向接触行为分析

研究轮轨切向接触行为的主要目的是确定轮轨切应力分布，以下将分别采用平面算法和曲面算法分析轮轨切向接触行为。

2.2.1 轮轨接触斑内接触角变化

轮轨接触斑内的接触角会影响自旋，从而导致纵横向刚性蠕滑率变化。平面算法考虑接触斑内的接触角恒等于接触点处的接触角，但实际上，接触斑内接触角会随着轮轨型面发生变化，尤其是轮缘与轨距角发生曲面接触时。分析轮对横移量分别为-6、7.77、9.5 mm 3种接触情况的接触角在接触斑内的变化情况，见图6。

图6 不同横移量下的接触角

由图6可知，轮对横移量为-6 mm时，接触斑宽度约为11.2 mm，接触斑内接触角变化幅度约为1.24°；轮对横移量为9.5 mm时，接触斑宽度约为0.85 mm，此时接触斑沿纵轴呈狭长状，接触斑内接触角变化幅度约为0.04°。踏面与轨顶发生接触或者轮缘与轨距角呈凸面接触时，变化幅度均较小，此时平面算法将接触斑内的接触角假设为与接触点处的接触角一致，不会产生较大误差。而轮对横移量为7.77 mm时,接触斑宽度约为11.1 mm，接触斑内接触角变化幅度达到了22.68°。根据图2和式(7)、式(8)知，接触角变化会影响接触斑内自旋，曲面算法考虑了真实接触角的变化，在轮缘与轨距角发生共形接触时，其纵横向蠕滑率会与平面算法相差较大，进而影响到切向力的大小和分布。

2.2.2 轮轨影响因子

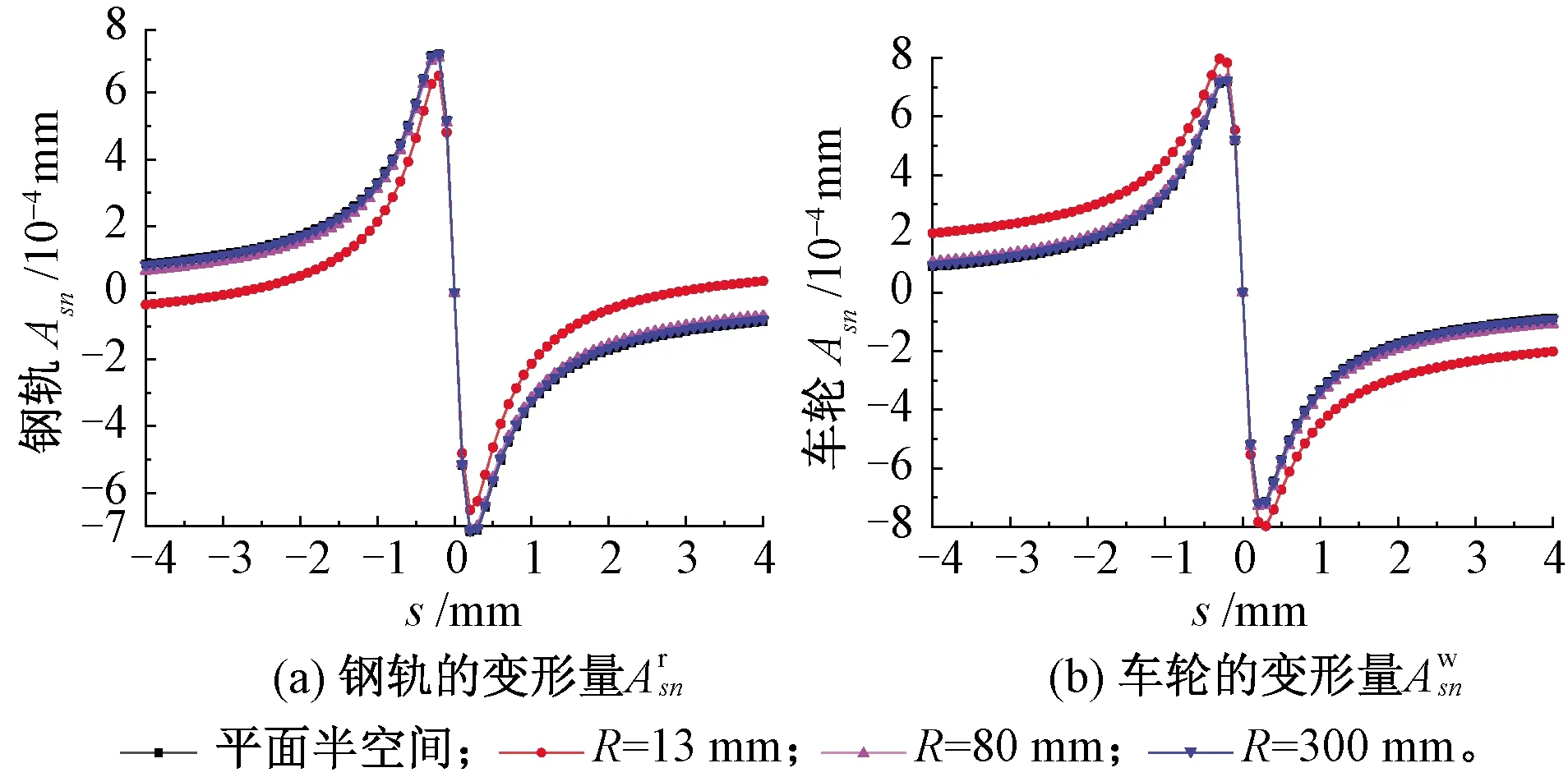
图7 不同曲率下钢轨和车轮的影响因子

由图7可知，车轮和钢轨曲率半径为300 mm时，曲面算法得到的车轮和钢轨变形量Asn几乎与平面算法完全一致；半径为80 mm时有轻微差别；然而半径为13 mm时差别较明显。原因是半径为300 mm时，接触点附近接触型面法向差异不大，即式(9)中α角小，导致曲面算法得到的影响因子与平面算法差异较小；当半径为13 mm时，α角大，从而导致2种算法得到的影响因子差异较大。此外，在相同的法向力下，车轮和钢轨的横向位移并不相同，轮轨间的相对位移会产生蠕滑现象，从而产生切应力。

2.2.3 蠕滑曲线

车辆动力学中，轮轨力是重要的参量，求解蠕滑力的基础是蠕滑率、蠕滑力关系曲线。由于3个工况中，轮对横移量为7.77 mm时接触斑内接触角变化最大，因此本节选择轮轨横移量为7.77 mm时的蠕滑率、蠕滑力关系曲线进行分析。为了得到曲面算法由于考虑变自旋所导致的蠕滑率、蠕滑力关系曲线与平面算法的差异，分别采用平面算法和曲面算法计算轮轨接触斑内的蠕滑率、蠕滑力关系曲线，仅改变接触点处的纵向或横向蠕滑率，即式(7)、式(8)中的εx或εy，纵坐标除以切向力边界10-6P使其无量纲化，结果见图8。图8(a)为纵向蠕滑率改变而横向蠕滑率为0的蠕滑曲线，图8(b)为横向蠕滑率改变而纵向蠕滑率为0的蠕滑曲线。

图8 蠕滑率、蠕滑力关系曲线对比

由图8可知，2种算法得到的蠕滑率和蠕滑力关系均表现出明显的非线性特征，这是由于蠕滑力受到库伦摩擦定律限制，当蠕滑率达到一定值时，接触斑进入全滑动状态，蠕滑力达到极限值。图8平面算法得到的纵向蠕滑力和横向蠕滑力在横坐标为0时纵坐标不为0是由于考虑了自旋的影响，且相对误差均在横坐标为0时最大，分别为9.1%和9.4%。2种算法得到的蠕滑曲线不同的原因是曲面算法考虑了接触斑内变自旋，即接触斑内接触角和滚动圆半径变化，而平面算法考虑恒定自旋，从而引起纵横向刚性蠕滑率的差异，蠕滑率、蠕滑力曲线的不同则会导致蠕滑力的不同。

2.2.4 轮轨切向接触应力大小及分布

分别采用平面算法和曲面算法计算横移量为-6、7.77、9.5 mm时的切向力，结果见图9。图9中，Xc为接触斑内沿纵向的坐标，Yc为接触斑内沿横向的坐标，颜色深浅代表切应力的大小，箭头代表切应力的方向。由图9(a)、9(b)、9(e)、9(f)可知，当轮对横移量为-6、9.5 mm时，平面算法和与曲面算法得到的切应力的大小和方向几乎没有差异。原因是这2种接触情况下，接触斑内接触角变化小，2种算法得到的纵横向蠕滑率差异较小。虽然横移量为9.5 mm时，轮缘与轨距角接触，轮轨型面接触半径大约为13 mm，曲面算法得到的影响因子与平面算法得到的结果差别较大，但是这种差别对接触应力的影响不大。由图9(c)、9(d)可知，当轮轨横移量为7.77 mm时，平面算法和曲面算法得到的切应力大小明显不同。曲面算法得到的最大切应力约为698 MPa，平面算法约为519 MPa，比曲面算法的结果大34.5%。原因是横移量为7.77 mm时，轮缘与轨距角发生共形接触，这时2种算法得到的影响因子差别较大,且此时接触斑内接触角变化大，从而使2种算法得到的纵横向蠕滑率差别也较大。基于以上的分析可知，影响因子和蠕滑率的综合影响导致2种算法的切应力结果差异较大，且主要是由于蠕滑率的影响。

图9 不同横移量下接触斑内切应力分布

为了更直观地体现出轮缘与轨距角发生曲面接触时2种算法得到的切应力分布差别，分析接触斑横坐标Yc为-7 mm断面上接触切应力沿接触斑纵向分布，结果见图10。由图可知2种算法得到的纵横向切应力差异较大。曲面、平面算法得到的最大纵横向切应力分别为257、36 MPa；平面算法分别约为452、78 MPa，平面算法得到的最大纵横向切应力分别比曲面算法的结果大75.9%、113.5%。由此可以看出2种算法的切应力大小及分布差异较大，这种差异会对轮轨磨耗深度的计算产生较大影响。

图10 轮对横移量为7.77 mm时的纵、横向切应力

2.3 轮轨接触斑内磨耗深度分布

分析发现2种算法在轮缘与轨距角发生共形接触时计算得到的轮轨接触行为差异较为明显，且车轮过小半径曲线时，轮缘与轨距角易发生共形接触从而加剧轮轨磨耗，因此本节采用2种算法分析轮缘与轨距角发生共形接触时的磨耗深度。利用平面算法和曲面算法计算得到轮轨间蠕滑率和切应力，然后采用USFD磨耗模型[17]预测磨耗深度，由图5分析可知，轮对横移量为7.77 mm时轮缘与轨距角会发生共形接触，因此本节以横移量为7.77 mm为例分析2种算法预测磨耗深度的差异。为了便于对比，将2种算法得到的磨耗深度除以平面算法的最大磨耗深度，进行归一化处理，沿接触斑横向坐标磨耗深度的结果见图11。

图11 横移量为7.77 mm时的预测磨耗深度

由图11可知，2种算法得到的最大磨耗深度不同，曲面算法得到的最大磨耗深度约为平面算法的93.5%；此外，2种算法得到的左侧接触斑磨耗范围也不同，平面算法的磨耗范围为-8.6～-5.9 mm，曲面算法磨耗范围为-9.5～-6 mm。其原因主要是2种算法得到的接触斑不同、切应力和蠕滑率大小和分布不同。可见当轮缘与轨距角发生共形接触时，2种算法得到的磨耗深度差异较明显。因此，建议采用曲面算法计算磨耗深度，以便更加精确地预测钢轨磨耗的演变。

2.4 考虑轮轨曲面接触行为的必要性分析

通过分析可知，轮缘与轨距角发生共形接触时平面算法的结果会产生较大误差，因此有必要采用曲面算法。虽然上文的分析中只选取了轮对横移量为7.77 mm这一个共形接触工况，但这不仅仅是特例。为了说明这个问题，分别采用平面算法和曲面算法计算了轮对不同横移量下的接触斑面积和最大法向应力，横移量从-6～12 mm，步进为0.5 mm，在7.77 mm附近加密取了7.76、7.78、7.79 mm，结果见图12。

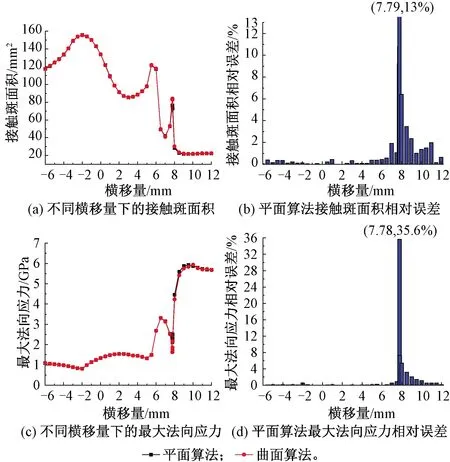
图12 不同横移量下的接触斑面积和最大法向应力及平面算法的相对误差

由图12(a)、12(c)可知，随着横移量的增加，接触斑面积大致呈减小趋势，最大法向应力大致呈增大趋势。但是在7.77 mm附近，接触斑面积先增大后减小，最大法向应力先减小后增大，这是由于轮缘与轨距角发生共形接触时接触斑面积会增大。此外，由图12(b)、12(d)可知，平面算法相对误差均集中在7.77 mm附近分布，接触斑面积相对误差最大约为13%，出现在横移量为7.79 mm处；最大法向应力相对误差最大为35.6%，出现在横移量为7.78 mm处。

综上所述，轮缘与轨距角发生共形接触时，接触斑形式是曲面，此时采用平面算法求解轮轨接触会产生较大的误差，为了更精确地分析轮缘与轨距角发生共形接触时的轮轨滚动接触行为，有必要采用曲面算法。

3 结论

为了更精确地计算轮缘与轨距角发生共形接触时的接触斑面积、接触应力，本文基于Kalker三维非赫兹滚动接触理论，对CONTACT数值程序的法向间隙、纵横向蠕滑率和影响因子进行修改使其可以考虑轮轨曲面接触斑。以S1002CN车轮踏面和CHN60钢轨型面为研究对象，对比分析了曲面算法与CONTACT在踏面与轨顶发生接触、轮缘与轨距角发生共形接触、轮缘与轨距角发生凸面接触这3种典型接触工况下的计算结果，得到如下结论。

(1)当车轮踏面与轨顶接触或者轮缘与轨距角呈凸面接触时，接触斑内沿横向各点法向差异较小，可以将接触斑看成平面，此时平面算法和曲面算法得到的法向间隙、接触斑面积和接触应力差异均较小。

(2)当车轮轮缘与轨距角发生共形接触时，接触斑内沿横向各点法向差异较大，导致采用2种算法得到的轮轨滚动接触行为差异也较大。主要体现在：平面算法得到的法向间隙比曲面算法得到的结果大，接触斑面积比曲面算法得到的结果小。因此，平面算法的最大法向接触应力和切向接触应力均比曲面算法得到的结果大。此外，2种算法得到的蠕滑率、蠕滑力关系曲线也不同。在该接触情况下，使用平面算法得到的结果会产生较大的误差，因此有必要采用曲面算法。

(3)将2种算法得到的蠕滑率和切应力用于计算轮缘与轨距角发生共形接触时的磨耗分布，发现其计算结果差异较大。因此建议这种接触情况下采用曲面算法计算磨耗，以便更精确地预测轮轨磨耗演变。

本文通过理论推导，提出了一种基于CONTACT边界元方法的曲面接触模型，初步调查了曲面接触特性对滚动接触解的影响，后续将进一步通过有限元方法对其有效性进行验证，并将其植入车辆-轨道耦合动力学程序，考虑曲面接触特性对车辆动力学行为的影响。