混凝土徐变的Gamma模型参数估计研究
陈梦成,杨 超,方 苇,温清清,许开成,黄 宏
(1.华东交通大学 土木建筑学院,江西 南昌 330013;2.省部共建轨道交通基础设施性能监测与保障国家重点实验室,江西 南昌 330013)
混凝土结构在土木工程和基础设施中应用广泛,服役期间混凝土在长期荷载作用下会产生徐变变形,并且随时间不断增长。徐变会引起桥梁结构性能退化,导致其服役时间未到设计寿命,提前失效。1996年9月26日,帕劳共和国的Koror-Babeldaob桥建成不到19年突然发生垮塌。专家分析,其倒塌的主要原因是混凝土徐变引起的跨中下挠过大。因此,Bažant等[1]在国际混凝土结构协会会议上呼吁人们要高度重视混凝土徐变及徐变效应问题。
目前,国内外对于混凝土徐变研究较多[2-7],但主要集中在确定性徐变问题上。事实上,影响混凝土徐变的因素有内在因素,如材料组分和材料性能等,也有外在因素,如环境与荷载等,这些因素大多是不确定的。另外,混凝土徐变也是随时间增长的。因此,混凝土徐变发展过程是一个单调非负、随时间增长的随机过程,传统的确定性计算方法已经不适用于混凝土徐变预测要求。赵人达等[8]、徐腾飞等[9]、Ma等[10]和余志武等[11]基于随机有限元和统计方法对混凝土徐变引起的桥梁变形进行了研究,均得到了非常有益的结果,推动了混凝土徐变研究进程,但这些研究成果尚未考虑徐变随时间的变化。1965年,Benjamin等[12]首次将混凝土徐变看作随机过程。1975年,Abdel-Hameed[13]提出采用随机Gamma过程建立结构性能随时间随机退化的模型。常用来描述随机过程的有预定义状态类别的Markov过程,其属无自相关随机过程类。Nootwijk[14]阐释了离散马尔可夫过程(如Markov链)和连续Markov过程(如Brownian运动)与Poisson、Levy和Gamma过程之间的差异性,并指出Gamma随机过程是一个单调、独立、非负退化增量的随机过程,适合模拟与时间相关的、渐变的结构性能退化过程,如裂纹、疲劳损伤、磨耗、腐蚀、收缩徐变等引起的结构性能退化过程。Pandy等[15]也进一步说明Gamma过程适用于捕捉这类过程。目前,国内外使用随机Gamma过程模拟随时间单调、缓慢增长过程的研究很多,如混凝土收缩和徐变[16-17]、疲劳裂纹扩展[18-20]、钢材锈蚀[21-25]和产品性能老化[19-20,26]等。但是,模拟混凝土徐变发展过程的论文屈指可数[16-17],且尚不够成熟。
本文首先采用Gamma随机过程对混凝土徐变发展过程进行建模,并将模型参数作为随机变量,根据它们的先验分布,导出其后验分布和后验估计;其次,基于尺度参数β后验估计值计算得到形状参数幂函数表达式中系数c的后验矩估计和极大似然估计值;最后运用累计误差平方和最小准则,结合应用仿真算例,对这几种估计方法进行对比。
1 混凝土徐变模型构建
1.1 Gamma过程
混凝土徐变是混凝土在恒定荷载作用下随时间递增而单调增长的变形。将混凝土在t时刻的徐变量定义为X(t),并且有X(0)=0,其随时间的增加而逐渐单调增长。因此,对任意时刻ti、tj,如果tj>ti,则必有X(tj)-X(ti)>0,符合随机Gamma过程的特点。这里使用Gamma分布来描述混凝土徐变量的随机性,使用随机Gamma过程来描述混凝土徐变量随时间变化的过程。
混凝土徐变量X的概率密度函数可用Gamma分布表示,具体为
(1)

假定形状参数α(t)为非负、右连续的实值函数,且t>0时,有α(0)=0。当Gamma过程形状参数α(t)>0和尺度参数β>0时,混凝土徐变随机过程{X(t):t≥0}可以看作是一个时间连续随机Gamma过程,且具有以下特征:
(1)当概率为1时,有X(0)=0。
(2)对所有τ>t≥0时,有[X(τ)-X(t)]~Ga(α(τ)-α(t),β),即X(τ)-X(t)服从Gamma分布。
(3)X(t)的增量是独立的,即对任意时间节点t1
因此,t时刻的混凝土徐变量X(t)的概率密度函数可以表示为
fX(t)(x)=Ga(x|α(t),β)=
(2)
由式(2)可得到混凝土徐变量的期望值和方差为
(3)
由于混凝土徐变为非线性过程,因此,它是一个非稳态Gamma随机过程。根据Noortwijk等[27]研究成果,Gamma随机过程模型中比例参数β为常数,形状参数α(t)可表示为幂函数形式,即
α(t)=c·tb
(4)
式中:c、b为参数
将式(4)代入式(2),Gamma模型中未知参数变为c、b和β三个。在通常情况下,Noortwijk[14]建议参数b取为常数,它取决于特定的退化过程。当b=1时,随机Gamma过程为稳态的,单调过程与时间为线性关系;若b≠1,随机Gamma过程为非稳态的,单调过程与时间为非线性关系。
1.2 模型参数的经典估计方法
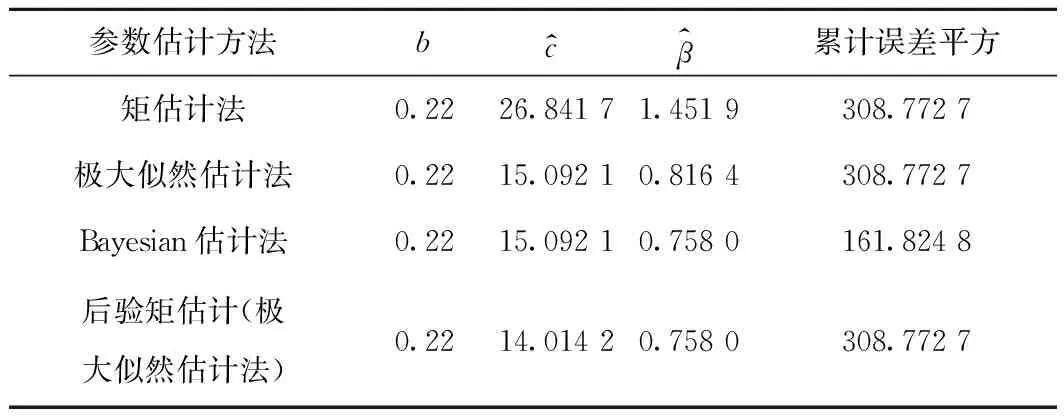
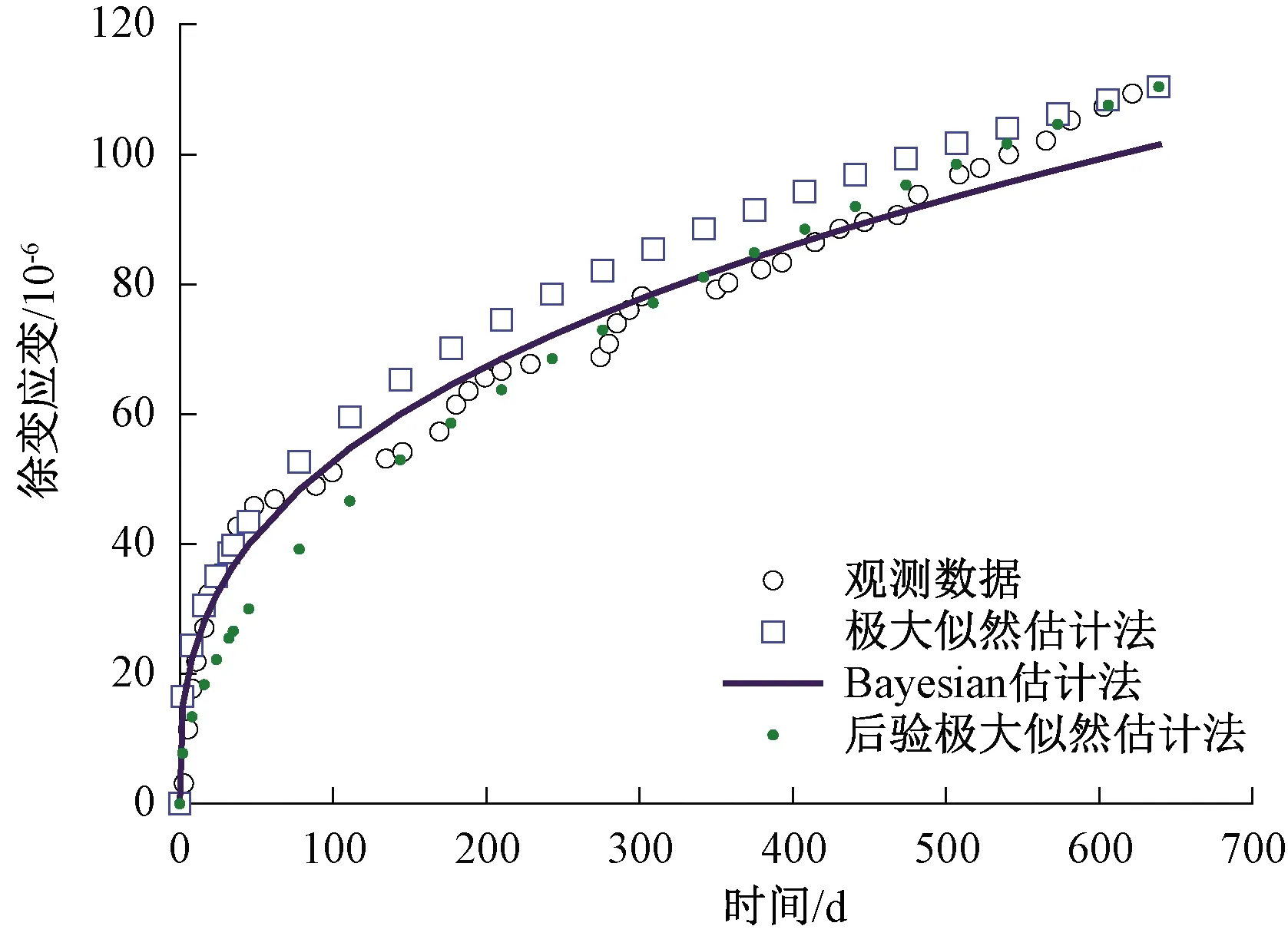
为使Gamma模型能解决徐变问题,需要运用统计学方法对模型中三个未知参数进行估计[28-29]。构建一组数据集,它由检测时间节点ti和相应混凝土徐变量的检测值xi组成(i=1,2,…,n),并且0=t0 1.2.1 矩估计法 依据大数定理,只要样本容量足够大,便可认为样本矩无限接近总体矩。因此可用样本一阶原点矩估计总体平均值,用样本二阶中心矩估计总体方差。 根据式(3),t时混凝土徐变量的期望值和方差可写为 (5) 当参数b已知时,通过变换,将日历时间t转化为换算时间z(t),即z(t)=tb后,非平稳随机Gamma过程可以很容易转化为平稳随机Gamma过程。对于所有时间t,如果混凝土徐变量的增量X(t+h)-X(t)的概率分布仅与h(h>0)有关,那么混凝土徐变量的随机变化过程就具有稳定的增量。将式(5)中日历时间t进行逆转换,即令t(z)=z1/b,则式(5)变为 (6) i=1,2,…,n。为了数学处理上的便利,同时令 (7) 对所有i=1,2,…,n,式(7)中混凝土徐变量增量Di满足形状参数为cwi和尺度参数为β的Gamma分布,并且D1,D2,…,Dn独立。注意到Xi、Di、Yi为随机变量,xi、δi、yi为相对应的检测值,那么对于每个时间节点i,Yi的一阶和二阶矩分别为 (8) 为便于理解,引入总换算时间内混凝土徐变量增量平均值定义,即 (9) 联立式(8)和式(9),可得 (10) (11) 由于E(Yi)=0,那么由式(7)右边第二项求期望值可得 (12) 根据式(10)~式(12),并对等式(11)两边求期望值,有 (13) (14) (15) 式(14)、式(15)表明,用矩估计法简单,而且容易计算。但是当参数b未知时,矩估计法将失去效用。 1.2.2 极大似然估计法 现在讨论模型形状参数c、b和尺度参数β的极大似然估计方法。首先建立混凝土徐变增量的似然函数,然后再对其两边取自然对数,并使自然对数似然函数取最大值。在混凝土徐变增量服从Gamma分布的总体中,检测(或抽样)到一组数据样本δi=xi-xi-1,i=1,2,…,n,独立且同分布。因此,混凝土徐变增量的似然函数是由其独立增量Gamma密度函数的乘积构成的,即 (16) 对式(16)两边取自然对数,有 (17) 为了使式(17)取得极大值,令 (18) (19) (20) 式中:ψ(a)为Digamma函数,由伽马函数对数求导得 (21) 其中,a>0。ψ(a)可使用Bernardo[30]提出的算法精确计算。 (22) (23) (24) (25) (26) 1.3.1 尺度参数β的Bayesian后验分布和估计 若考虑未知参数的不确定性,则需要使用Bayesian定理[14]。Bayesian定理是为解决概率问题而提供的一种数据学习方法。记ti时刻的混凝土徐变增量为随机变量Di,δi为来自Di的样本数据或检测数据。由前面讨论可知,它们为独立同分布,均服从Gamma分布,相对应的有未知形状参数为b、c和尺度参数β,其中参数b一般是已知的常数(与特定的混凝土徐变过程有关)。在Bayesian理论中,c和β不再是未知参数,而是随机变量,可以根据经验和已完成的试验或检测历史数据确定,有明确的概率分布,是先验分布,可以是有信息分布或无信息分布。假定参数c和尺度参数β是相互独立的,那么根据Bayesian定理,有 (27) 式中:L(δ1,…,δn|c,β)为检测数据δ1,…,δn的似然函数,分布形式已由式(16)给出;π(c,β)为获得新检测数据δi(i=1,2,…,n)前参数(c,β)的先验概率密度(先验分布);π(c,β|δ1,…,δn)为获得新检测数据δi(i=1,2,…,n)后(c,β)的后验概率密度(后验分布)。 由此可见,一旦获得新的检测数据样本δi,就可利用Bayesian定理式(27)更新先验分布而得到后验分布。下面讨论当c为定值时尺度参数β的后验分布和估计的解析求解方法。 当参数c已知时,尺度参数β的先验分布考虑采用共轭先验形式,即π(β|c)服从Gamma分布,记为β~Ga(a,λ),其中a为形状参数,λ为尺度参数。由式(27)有 π(β|c,δ1,…,δn)∝L(δ1,…,δn|c,β)·π(β|c)= L(δ1,…,δn|c,β)·π(β)= (28) (29) 式中:B为未知的随机变量。 当参数c未知且为定值时,依据式(14)或式(22),尺度参数β依赖于c,因此,β的形状参数和尺度参数可以分别写为:a(c)和λ(c)。当选择a(c)=cτb(τ>0)和λ(c)=λ时,并且c取定值时,尺度参数β的后验估计值可以表示为 (30) 由式(5)可知,t时混凝土徐变量X(t)的期望值E(X(t))=ctb/β,在检测到一组新数据δi(i=1,2,…,n)后,t时混凝土徐变量预测值可表示为 (31) 1.3.2 后验矩估计 若b未知时,由于此时还有2个未知量c和β,矩估计不再适用。 1.3.3 后验极大似然估计 Bažant收集了全球大量的徐变试验数据并建立徐变数据库,本文挑选其中一根加载龄期为2 d的试件,试验测得混凝土徐变观测数据xi(i=1,2,…,15),并且x1=0[31]。 2.1.1 b已知 考虑形状参数为时间t的幂函数形式,即α(t)=c·tb。根据Bažant获得的徐变试验数据xi,可计算得到徐变增量δi,并且假定b是已知的,b=0.22。分别采用矩估计法(式(14)、式(15))、极大似然估计法(式(22)、式(23))、Bayesian估计法、后验矩估计法和后验极大似然估计法进行参数估计。 (1)根据b=0.22,使用矩估计法、Newton-Raphson迭代法,求解得到参数c和尺度参数β的经典估计值,并将其代入式(25),计算得到混凝土徐变随时间变化数据。 (2)根据b=0.22,用极大似然估计法、Newton-Raphson迭代法,求解得到参数c和尺度参数β的经典估计值,并将其代入式(25),计算得到混凝土徐变随时间变化数据。 5种算法下素混凝土徐变模拟结果比较见图1。从图1可知,5种估计方法模拟结果均与试验观测数据吻合较好,其中,因式(14)和式(22)的缘故,经典矩估计、极大似然估计方法和后验矩估计、极大似然估计得到的曲线重合。5种算法下damma模型参数估计见表1。 图1 5种算法下素混凝土徐变模拟结果比较 表1 5种算法下Gamma模型参数估计值 图2为5种估计算法与试验观测值误差平方的比较,由图2可知,用经典矩估计和极大似然估计与用后验估计和极大似然估计得到的徐变计算值随徐变时间增长波动较大,而用Bayesian估计得到的徐变值波动较小,波动相对比较平缓,且Bayesian估计的累计误差平方和最小(见表1),因此,用Bayesian估计的效果最好,优于其他4种方法。 图2 5种算法下素混凝土徐变误差平方比较 2.1.2 b未知 在b未知的情况下,有3个未知量c、b和β,用矩估计法无法求解。此时,4种估算法,只剩下3种,即经典极大似然估计法、Bayesian估计法和后验极大似然估计法。 表2 3种算法下Gamma模型参数估计值 图3 3种算法下素混凝土徐变模拟结果比较 3种参数估计算法下素混凝土徐变模拟结果的误差平方比较见图4。 图4 3种算法下素混凝土徐变误差平方比较 由图3可以看出,3种估计算法均和试验观测值接近,但由图4和表2可知,经典极大似然估计误差最大,后验极大似然估计次之,Bayesian估计最小。因此,Bayesian估计和后验极大似然估计优于经典极大似然估计,其中Bayesian估计最优。 2006年,陈政清等[32]进行一批圆钢管高强混凝土徐变试验,选取其中8号钢管混凝土试件进行徐变发展过程模拟。试件尺寸及材料等参数参考文献[32]。在本实例中,仍然假定钢管混凝土徐变量X(t)~Ga[α(t),β];徐变量变化的Gamma随机过程为时间幂函数形式,即α(t)=c·tb,其中:c和b均为待确定的确定性参数;尺度参数β为随机变量。 在模拟钢管混凝土徐变发展过程中,采用类似2.1.2节的算法,用极大似然估计法得到钢管混凝土徐变Gamma模型的初始参数c和b的估计值,见表3。假定尺度参数β的先验分布仍然服从Ga(a(c),λ(c))分布,形状参数a(c)=cτb,并取τ=2>0,尺度参数λ(c)=3。 表3 3种算法下Gamma模型参数估计值 3种估计算法的钢管混凝土徐变随时间变化的模拟结果见图5。图6为3种参数估计算法下钢管混凝土徐变模拟结果的误差平方比较。 图5 3种算法下钢管混凝土徐变模拟结果比较 图6 3种算法下钢管混凝土徐变误差平方比较 由图5可以看出,3种估计算法的模拟结果均接近试验观测值,但由图6和表3可知,Bayesian估计和后验极大似然估计的模拟结果优于经典极大似然估计,其中尤以Bayesian估计为最佳。 本文根据混凝土徐变发展过程特点,建立了基于非稳态Gamma随机过程的混凝土徐变随机模型,Gamma随机过程反映了混凝土徐变量是时间的幂函数形式。应用矩估计法、极大似然估计法和Bayesian估计法,融合试验观测数据,对Gamma随机过程参数进行估计,从而实现了对混凝土徐变过程的模拟。在此基础上,本文还应用Bayesian理论得到了后验的参数估计方法,并将经典参数估计法的模拟效果和后验参数估计法的效果进行比较,得到如下结论: (1)提出的五种参数估计法的模拟效果均较好,均能和试验观测数据相吻合。 (2)当参数b已知时,后验的矩估计和极大似然估计的混凝土徐变效果与经典的矩估计和极大似然估计的效果完全相同,Bayesian估计的效果优于矩估计和极大似然估计的效果。 (3)当参数b为未知时,矩估计法不再适用;Bayesian估计法和后验极大似然估计法的模拟结果均优于经典极大似然估计,其中以Bayesian估计法的模拟结果为最佳。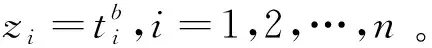



1.3 模型参数的后验估计方法
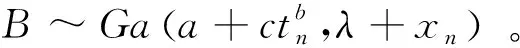

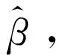
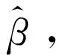
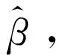
2 实例应用与讨论
2.1 素混凝土徐变
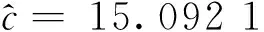
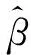


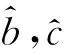



2.2 钢管混凝土徐变

3 结论

