基于载荷相互作用效应的Corten-Dolan改进模型

刘其鹏，高月华，李永华

(1.大连交通大学 土木工程学院,辽宁 大连 116028；2.大连交通大学 机车车辆工程学院,辽宁 大连 116028；3.南昌航空大学 航空制造工程学院,江西 南昌 330063)

随着高速铁路的发展，轨道车辆关键部件的疲劳破坏问题突显出来[1-3]。结构的疲劳破坏影响轨道车辆的运输安全，甚至可能会造成难以估量的严重后果。因此，寻求有效的疲劳寿命预测方法具有非常重要的工程意义。

对于轨道车辆的实际运营状态，其结构的承载状态多为变幅载荷作用。在变幅载荷作用下，车辆结构的疲劳累积损伤计算及寿命预测极为重要。疲劳累积损伤理论模型主要分为线性累积损伤理论和非线性累积损伤理论两大类[4]。线性累积损伤理论以Miner法则为代表，假定疲劳损伤与循环比成线性关系，且与载荷等级次序无关。由于其概念清晰，公式简单，许多著名的疲劳设计和评估标准仍在使用[5]。然而，Miner法则没有考虑载荷次序及相互作用效应，导致其对变幅载荷下疲劳寿命的预测精度较低[6]。

与常幅载荷相比，变幅载荷下疲劳损伤演化的最大特点在于载荷之间的相互作用效应对疲劳寿命的影响显著。载荷之间的相互作用效应是指疲劳损伤与应力加载历史的相关性[7]，即当前载荷下所产生的损伤不仅与当前状态相关，而且与前序的载荷大小、加载次序等密切相关。轨道车辆结构及部件承载着比较复杂的变幅载荷作用，进行疲劳寿命预测时，载荷间的相互作用是不可忽视的。

为了提高疲劳寿命预测的准确度，学者们提出了诸多非线性累积损伤模型[6,8]，其中Corten-Dolan模型[9]能够考虑小载荷的影响，在工程中得到了较多的关注和应用[10-17]。Corten-Dolan公式中的参数d的合理确定是该模型理论和应用的关键所在，最早参数d认为是材料常数，通过二级加载试验确定[9]。后来学者们发现该参数不仅与材料属性有关，还与应力水平[10]、剩余强度[12]、加载次序及载荷作用效应[13,17]、损伤程度和应力状态[15-16]等密切相关，并提出了相应的改进模型。这些Corten-Dolan改进模型中关键参数d能体现载荷间的相互作用，但是针对载荷幅值及加载顺序变化的情况，其疲劳寿命的预测结果仍具有较大的分散性，需进一步深入研究。

作为轨道车辆结构疲劳寿命预测的基础性研究，本文对Corten-Dolan公式中参数d的表达式进行深入分析，在考虑小载荷、损伤程度和应力状态的基础上引入应力比的幂函数以表征载荷加载次序及载荷作用效应的非线性影响，从而建立了改进的Corten-Dolan非线性累积损伤模型。基于三种常用材料的变幅加载试验数据，应用全数据建模方案对本文改进模型的预测精度进行了验证，并与既有模型进行了对比分析。此外，提出了部分数据建模-验证的验证方案，从应用的角度考查本文改进模型对未知数据的预测能力。

1 Corten-Dolan模型及既有改进模型

根据Corten-Dolan模型，常幅载荷作用下的疲劳损伤公式为

D=mrna

(1)

对于变幅载荷情况，临界损伤值通常用最大应力σ1单独作用下疲劳破坏的损伤值表示为

(2)

变幅载荷作用下，各级载荷作用产生损伤的总和达到临界值时材料就发生疲劳破坏，因此有

(3)

式中：i表示第i级载荷。

Corten和Dolan基于上述损伤公式，结合冷拔丝钢的大量两级试验，并对理论公式做出简化后，得到两级应力下的寿命预测公式

(4)

式中：Ng为构件在两级载荷作用下总的循环次数(寿命)；N1为构件在1级(最大)应力单独作用下的寿命；α为1级应力作用的循环数占总循环数的比例。考虑到损伤发展速率正比于应力水平，Corten-Dolan进一步将上式中的损伤比项改写为应力比的形式，即

(r2/r1)1/a=(σ2/σ1)d

(5)

式中：d为参数。因此两级应力循环下的寿命预测公式为

(6)

Corten-Dolan认为上式可以直接推广到多级应力情况，即

(7)

为了方便公式在后续叙述和应用中的方便，上式中的σ1、N1分别用σmax、Nmax替代，表示多级载荷中的最大应力和最大应力单独作用下的疲劳寿命。

依据Miner线性损伤累积理论，可以给出类似的多级变幅载荷下疲劳寿命预测公式[10]

(8)

式中：p为根据等幅加载试验得到的常数。

对比式(7)、式(8)可以看出，二者的差别仅在于指数项，前者为d后者为p。对于变幅加载情况式(8)给出的寿命预测结果通常误差较大[10-16]。因此，如果式(7)中d不能恰当地给定，其预测结果也一定会很差。所以，参数d的合理表示和确定成为Corten-Dolan公式应用的关键。文献[16]中将其定义为包含循环次数和应力状态的函数

(9)

式中：ni表示第i级应力实际作用的循环次数；Ni表示第i级应力对应的常幅疲劳寿命；γ为材料相关的常数，可根据不同的试验数据结合疲劳失效判据拟合确定。文献[17]中进一步考虑了应力比的影响，给出

(10)

2 Corten-Dolan改进模型

2.1 Corten-Dolan模型的深入分析

从式(1)可以看出，Corten-Dolan模型通过参数a构建了损伤值与循环数之间的非线性关系，参数r既要体现应力水平对损伤的影响，还要能考虑各级应力之间相互作用的影响。式(5)将损伤系数转化为应力水平的表达式，该过程将参数a、以及应力间相互作用的影响均转化到参数d中进行考虑。此外，从式(6)、式(7)中也可以看到，分母中的底数项只有各级应力与最大应力之间的相比项σi/σmax，因此各级应力之间的相互影响只能通过指数d来考虑。

综上，将参数d视为简单的材料常数很难确定合理的d值。Corten-Dolan模型中参数d的合理确定，需要考虑三方面因素：①材料属性；②损伤与循环(或循环比)之间的非线性关系；③载荷之间相互作用效应的影响。一个合理的途径是将d值表示为一个函数，将以上因素分为多项变量进行考虑。模型式(9)中通过引入参数γ考虑了材料属性的影响，通过引入循环比ni/Ni的e指数考虑了当前损伤与循环比之间的非线性关系。模型式(10)则通过引入前后两级加载的应力比来考虑加载次序的影响，也在一定程度上体现了载荷之间的相互作用效应，使得模型对变幅载荷作用下疲劳寿命预测的可信度得到了提升。但是参数d的确定仍需进一步深入研究和改进，特别是对载荷之间相互作用效应的考虑方面。

2.2 考虑载荷间相互作用的Corten-Dolan改进模型

变幅载荷下疲劳损伤演化及寿命预测的关键就在于载荷之间的相互作用效应的考虑。一个有效的方案应当包含两方面：①要有一个可靠的度量参数；②要对该参数的影响进行充分考虑。

考虑到通过应力比的形式来体现载荷间的相互作用效应具有良好的预测性能[18]，本文改进模型中亦采用应力比作为基本变量对参数d进行修正。既有的研究工作显示载荷间的相互作用效应对结构累积损伤的影响并不是简单的线性关系，而是复杂的非线性关系[7,19-20]。因此，在既有Corten-Dolan模型考虑小载荷、损伤程度和应力状态的基础上，引入相邻两级应力比的幂函数对关键参数d进行修正以表征载荷间相互作用效应的非线性影响。综上，给出参数d的改进表达式为

(11)

式中：当i=1时，σi/σi-1=1。基于该式，改进的疲劳寿命预测模型为

(12)

由式(12)可以看出，当相邻载荷为先低后高的载荷加载时，疲劳寿命非线性增加；当相邻载荷为先高后低的载荷加载时，预测寿命非线性减小。

通过进一步分析，引入参数k可将式(9)～式 (11)中的参数d的表达式进行统一，表示为

(13)

式中：k=0时对应文献[16]所提出的改进式(9)；k=1时对应文献[17]所提出的改进式(10)；而k=2时对应本文所提出的改进模型式(11)。

3 算例及对比分析

为验证本文Corten-Dolan改进模型的有效性及对未知数据的预测能力，基于热轧16Mn钢[21]、标准45号钢和标准16Mn钢的试验数据[22]进行疲劳寿命预测，并将不同模型的预测结果进行对比分析。热轧16Mn钢两级载荷下的疲劳损伤试验在旋转弯曲疲劳试验机上进行，采用的大圆弧试样的棒材[21]。标准45号钢和标准16Mn钢的试验在PLD-10型10 t高频疲劳试验机上进行，采用大圆弧试样的棒材，为恒应力幅和对称加载[22]。三种材料的试验温度均为室温，试验方法为先在第一级应力水平下作用n1次, 然后第二级应力接着作用直到破坏，得到第二级应力下的剩余循环次数。

各材料的试验数据见表1，其中热轧16Mn钢和标准45号钢的试验数据载荷次序发生变化，而幅值没有变化(如热轧16Mn钢：高幅载荷为394 MPa，低幅载荷为345 MPa)。而对于标准16Mn钢的试验数据，在载荷次序发生变化的同时载荷幅值也发生了变化。对于高-低载荷加载模式1～模式5，高幅载荷为562.9 MPa，低幅载荷为392.3 MPa；对于低-高载荷加载模式6～模式8，高幅载荷为392.3 MPa，低幅载荷为372.7 MPa。这种载荷幅值及载荷次序均变化的加载模式与工程实际的载荷情况更加一致。

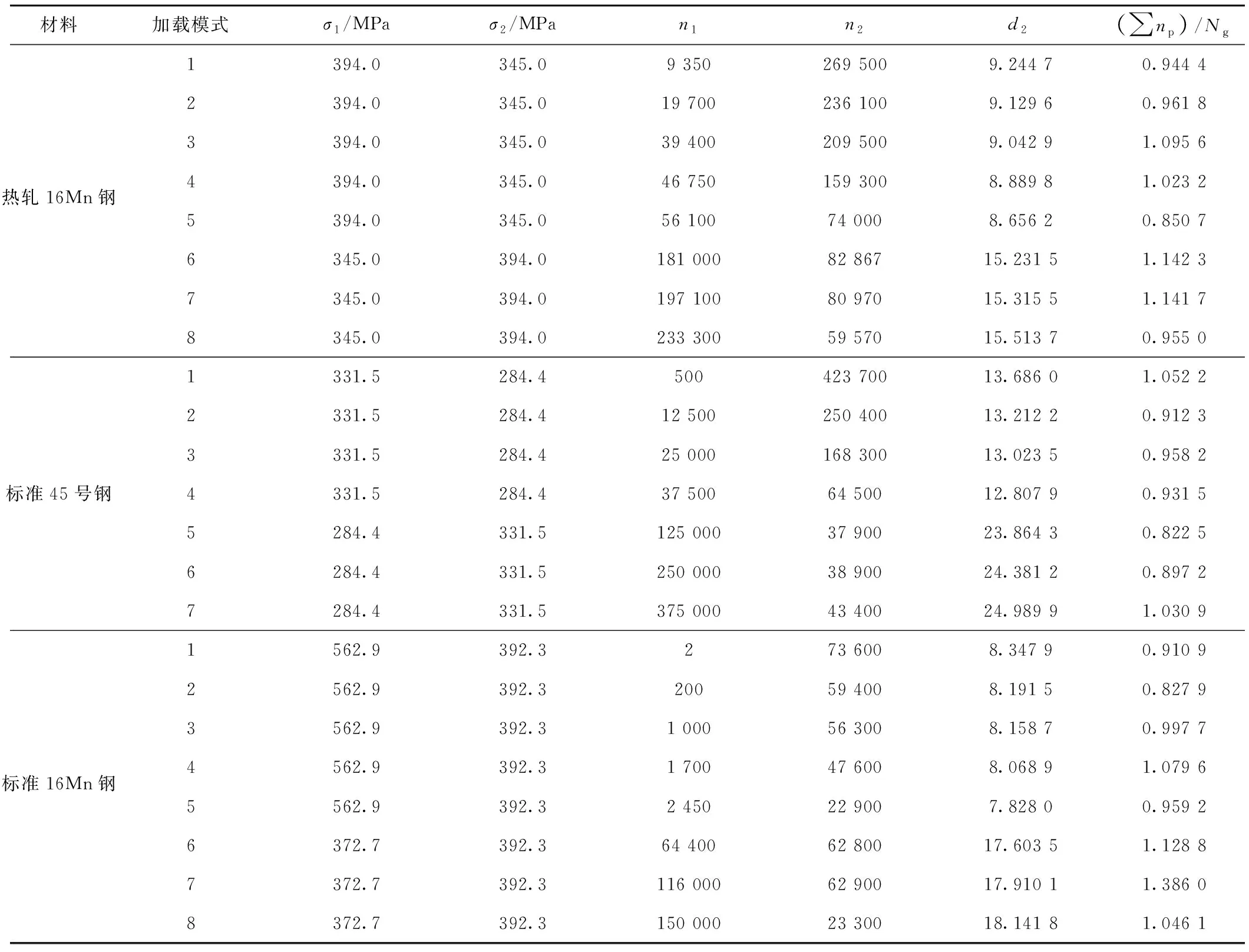
表1 不同材料基于本文改进模型的寿命预测结果

3.1 疲劳寿命预测结果的对比分析

依据式(12)，基于热轧16Mn钢、标准45号钢以及标准16Mn钢的全部试验数据对参数γ进行反演分析(全数据建模方案)，并计算相应的参数d和寿命预测结果。表1给出了热轧16Mn钢和标准45号钢的寿命预测结果。d2为式(13)k=2时的值，(∑np)/Ng表示试验寿命与预测寿命的比值，二者均为无量纲量。由表1结果可以看出，本文模型的预测结果比较接近试验结果,具有较高的预测精度。

针对热轧16Mn钢、标准45号钢以及标准16Mn钢材料，将本文改进模型对疲劳寿命的预测结果与文献[16-17]中模型的预测结果进行了对比，见图1。

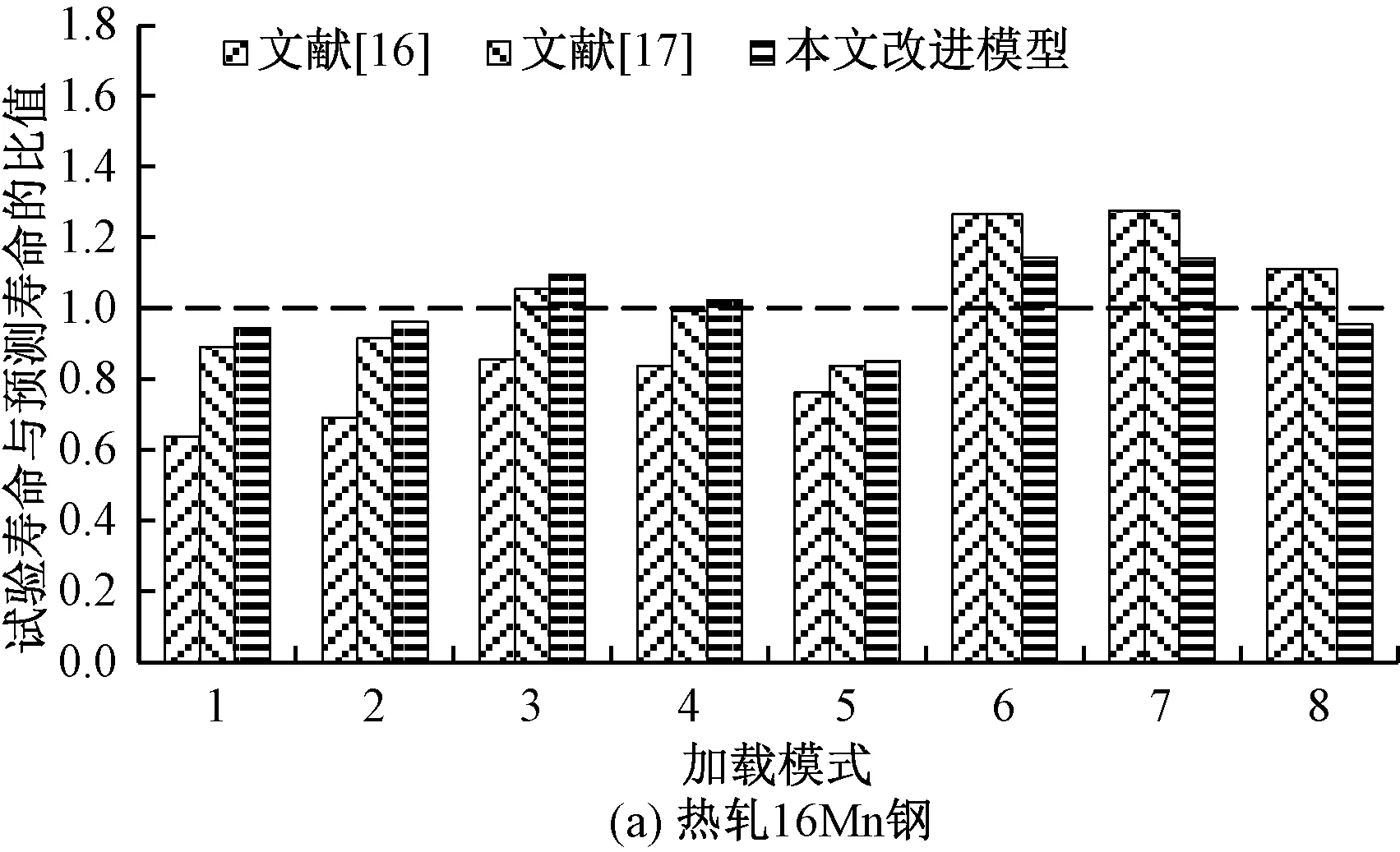
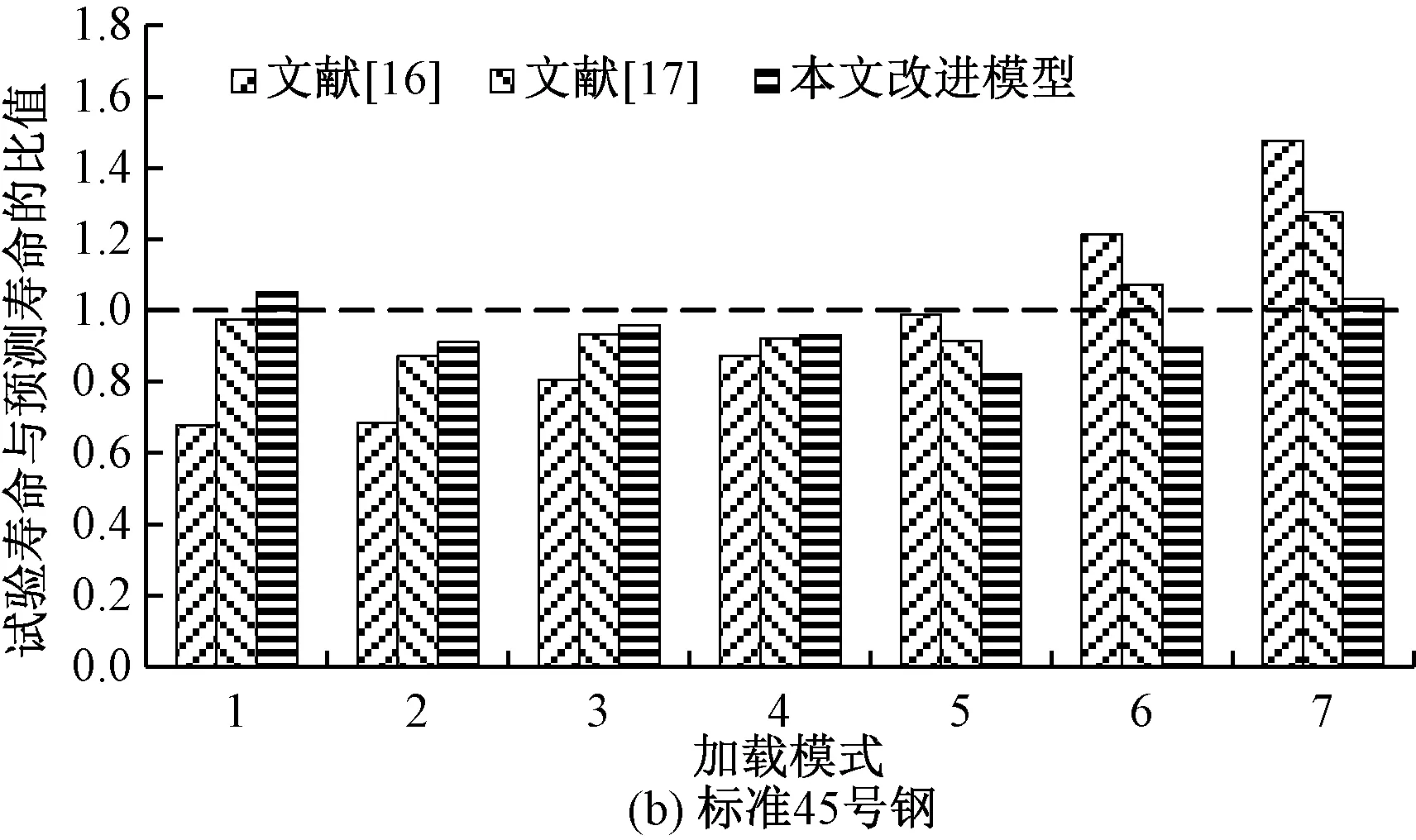
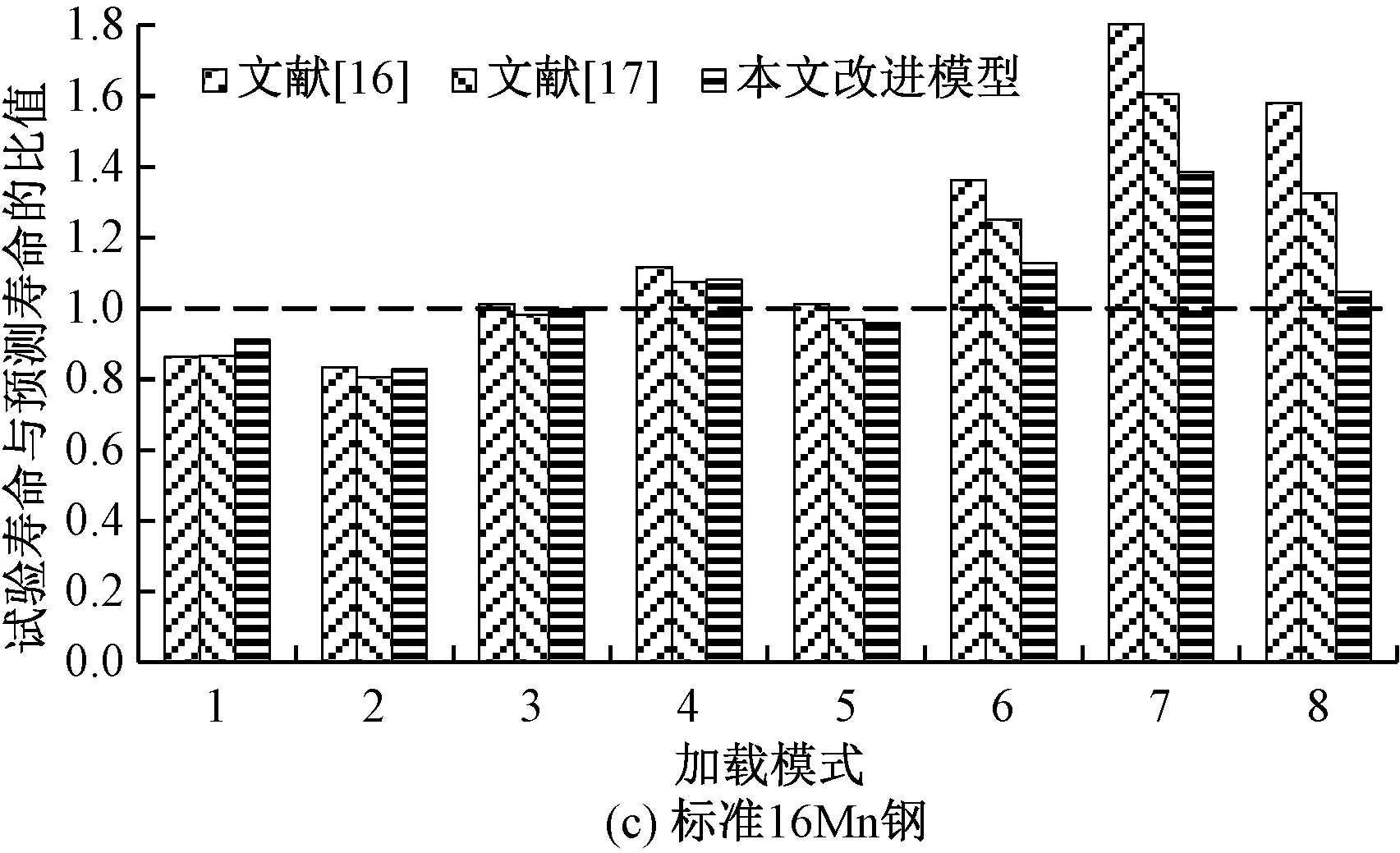
图1 采用不同模型预测疲劳寿命对比

从图1(a)可以看出，对于热轧16Mn钢，前5种加载模式(载荷由高到低)下，本文改进模型与文献[17]中模型的预测结果比较相近，预测精度均显著高于文献[16]模型的预测结果。对于后3种加载模式(载荷由低到高)，本文改进模型的预测结果显著优于文献中模型的预测结果。

从图1(b)可以看出，对于标准45号钢，本文模型的预测结果最优，略优于文献[17]的预测结果，明显优于文献[16]的预测结果。进一步对比文本模型与文献[17]模型结果发现，对于高-低的载荷加载模式(模式1—模式4)2种模型的预测结果相近；而对于低-高的载荷加载模式(模式5—模式7)，本文模型预测结果略优。

从图1(c)可以看出，对于标准16Mn钢，本文模型预测结果明显最接近试验值。对于高-低的载荷加载模式(模式1—模式5)，3种模型的预测结果比较相近；而对于低-高的载荷加载模式(模式6—模式8)，本文模型预测结果最优，文献 [17]中模型的预测结果次之，文献 [16]中模型的预测结果的误差较大，工程上已难以接受。

综上，各模型预测结果的对比分析显示了本文改进模型对变幅载荷下结构的寿命预测是比较有效的。尤其针对载荷次序变化的同时载荷幅值也发生变化的情况，本文改进模型的预测精度明显优于文献中既有模型的预测精度，这说明本文改进模型能够较好地表征变幅载荷下载荷相互作用效应的影响。

3.2 对未知数据预测能力的对比分析

既有的工作应用建立预测模型的试验数据对预测模型进行了验证，并没有应用额外的试验数据对所得的预测模型进行验证，难以保证预测模型的实际应用性。基于此本文从实际应用的角度出发提出了一种部分数据建模方案，该方案是将试验数据分为两组，一组为建立预测模型的数据，为模型已知数据；另一组为验证预测模型的数据，为模型未知数据。该方案能对模型对未知数据的预测能力进行有效的验证，能够检验预测模型的工程应用可行性。

为有效地检验预测模型对载荷相互作用敏感度，本文将载荷先高后低的试验数据作为模型已知数据，载荷先低后高的数据为模型未知数据。即，建模所用数据中不包含载荷次序及幅值变化的任何信息。

对于热轧16Mn钢、标准45号钢及标准16Mn钢的试验数据，基于已知数据(载荷先高后低)进行预测模型的建立和验证，并将本文改进模型与文献既有模型的预测结果进行对比，详细数据见表2。对于建立预测模型的已知试验数据，3种模型的预测结果几乎一致，表中仅列出了模型未知数据的预测结果。

表2 不同材料数据建模的预测结果对比

不同模型的预测结果对比见图2。由表2和图2可以看出，对于建立模型的已知试验数据，3种模型的预测结果几乎一致，都比较接近试验值。而对于未参与建模的未知数据，各模型给出的寿命预测值差别较大，而本文模型得到预测结果接近试验值，预测精度较高。文献[16]模型的预测误差较大，难以应用于工程实际。

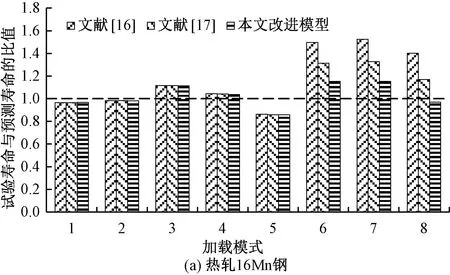
图2 不同材料部分数据建模的预测结果对比

该对比分析的建模数据不包含载荷次序及载荷幅值变化的任何信息，而本文改进模型却能比较准确地预测载荷次序和幅值变化加载模式下的疲劳寿命，说明本文改进模型能够充分体现载荷相互作用效应对疲劳寿命的影响，有较好的实际应用性。

4 结论

本文针对变幅载荷下结构的疲劳寿命预测，建立了改进的Corten-Dolan累积损伤模型，总结如下。

(1) 在既有Corten-Dolan模型考虑小载荷、损伤程度和应力状态的基础上，引入前后两级载荷应力比的幂函数对参数d进行修正，建立了考虑载荷之间相互作用非线性效应的Corten-Dolan模型，可有效地进行疲劳寿命预测。同时，引入参数k将此类改进模型表达式进行了统一。

(2)通过应用全数据建模方案对本文改进模型的疲劳寿命预测性能进行了验证，并与既有模型预测结果进行了对比分析。结果表明本文改进模型预测精度有所提高，尤其针对载荷加载次序及载荷幅值均变化的情况，本文模型预测结果明显优于既有模型。

(3)从实际应用角度出发，应用部分数据建模方案对本文改进模型的预测能力进行了验证。结果表明本文改进模型不仅能有效地提高疲劳寿命预测的精度，而且能够在载荷加载次序及幅值变化未知的情况下较为准确地预测疲劳寿命。这说明本文改进模型能更好地表征加载次序以及载荷幅值变化等载荷相互作用效应对疲劳寿命的影响，验证了本文改进模型的工程应用可行性。

(4)本文虽未考虑试验数据的离散性影响，但预测模型的结果对比分析已经充分表明了本文改进模型具有良好的预测能力，为轨道车辆结构的疲劳寿命预测提供了更好的理论基础。