基于RS-RBFNN的建筑工程造价预测模型

徐文慧，申建红,2，*，陈 雪，万索妮

(1.青岛理工大学 管理工程学院，青岛 266525；2.山东省高校智慧城市建设管理研究中心，青岛 266525)

准确的造价预测不仅有助于建设单位做出投融资决策，还能降低建设过程中造价超支的可能性.为进一步提高造价预测的精确度，学者们进行了广泛研究[1-3].其中，BP神经网络(Back Propagation Natural Net，BPNN)具有较强的自主学习能力和自我适应能力，能够准确地处理多因素和非线性问题，因此被广泛地应用于工程造价预测领域.蒋红妍等[4]针对高层住宅工程造价管理的难点及传统造价估算方法存在的不足，采用灰关联分析与粒子群优化的BP神经网络相结合的方法，实现了对高层住宅造价的快速估算.杨无疆等[5]选取6个工程特征类目作为BPNN的输入向量来预测工程造价，并通过实例验证了该方法的精确性和有效性.梁喜等[6]考虑了决策者判断的不确定性，将模糊数学与AHP方法相结合，筛选出与工程造价有较大相关性的工程特征指标，并把这些指标数据作为BPNN的输入集来预测造价，最后通过实例证明了该模型能有效地提高工程项目造价预测的精确度.然而，由于工程造价预测需要的初始数据较多，过多的数据输入维数会增加BPNN结构的复杂性，从而降低网络的拟合速度，甚至陷入局部极值.不同于全局逼近的BPNN，径向基函数神经网络(Radial Basis Function Natural Net，RBFNN)是1种局部逼近的网络，这一特性不仅使其具有更简单的结构和更快的学习收敛速度，而且避免了局部最优问题的出现，克服了BPNN的缺点.刘书贤、严薇等分别将RBFNN与BPNN用于工程造价的预测，并通过案例分析结果的对比，得出了RBFNN更适合于造价的预测的结论[7-8].

工程造价预测通常是预先收集已建类似工程的造价特征指标数据，然后通过一定的数学模型进行分析预测待建工程的造价.但是收集的特征指标数据之间通常存在大量的冗余信息，使得数据噪声较大，而RBFNN对数据噪声的敏感性不高，若不对数据噪声进行弱化处理，会降低RBFNN的学习拟合速度以及预测的精确程度.粗糙集理论(Rough Set Theory，RS)是波兰学者PAWLAK Z于1982年提出的一种处理不确定知识的数学工具，其属性约简功能在保留重要信息的前提下可简化数据并消除变量之间的冗余信息.因此，将RS作为RBFNN的数据降噪工具，找出与工程造价相关性较大的影响因素，剔除非主要影响因素，减少RBFNN的输入数据维数，就能进一步缩短网络的训练时间并提高它的预测准确性.

本文利用RS和RBFNN的优势互补特性，将两者有机结合用于工程造价的预测.首先，利用RS理论对影响工程造价的因素进行约简，减少RBFNN输入数据的维数；其次，将约简后的数据作为输入，总造价作为输出，构建RS-RBFNN模型进行造价预测；最后通过比较不同预测方法的预测结果偏差以及预测速度，得出了RS-RBFNN模型更适合于工程造价预测的结论.

1 研究方法

1.1 粗糙集

粗糙集理论是PAWLAK Z提出的1种处理不确定性、模糊性和不一致性问题的智能算法[9].它能够对各种不完备的信息进行分析和处理，从中发现隐藏的知识，揭示潜在的规律.粗糙集理论的属性约简功能可有效降低数据的噪声，简化数据维数.利用RS理论将获取的造价相关数据构成1个造价决策系统，在不改变系统决策能力的前提下，根据不同特征指标对总造价的重要程度，去除掉非关键指标数据，保留关键指标数据，以此简化RBFNN的输入.具体的属性约简步骤如下：

1) 外部数据获取形成决策表.将工程特征指标作为条件属性，工程总造价作为决策属性，构造原始造价数据决策表，决策表如式(1)所示：

S=(U,A,V,f)

(1)

式中：U为论域；A=C∪D，C是条件属性工程特征指标的集合，D为决策属性总造价的集合，2种属性的并集构成非空有限集合A；V是属性集的V=∪(Va)，Va∈A，Va集合，且是属性a⊂A的值域；f:U×A→V，f(xi,a)∈V是1个信息映射函数，赋予每个对象相应的信息值.

2) 属性值离散化.利用粗糙集进行属性约简有一定的前提条件，即决策表中的属性值必须是离散的，所以需要提前对决策表中的属性值进行离散化处理.离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小，从而提高算法的时空效率.

3) 属性约简.数据离散化处理后即可以进行属性约简，将约简后的最简属性集作为RBFNN的输入向量，不仅可以降低RBFNN的计算复杂度，减少运行时间，还能提高RBFNN的预测精度.

1.2 RBF神经网络

RBFNN是1种局部逼近的前馈式神经网络.RBF指的是径向基函数，是由POWELL于1985年提出的.1988年，MOODY等将RBF函数与神经网络相结合，自此，RBFNN得到了发展和应用[10].RBFNN不仅有较快的学习收敛速度，而且泛化能力好，与目前广泛使用的BPNN相比，RBFNN具有最佳逼近和全局最优的性能，能够很好地处理非线性问题，且不存在局部最优问题，所以RBFNN更适合于工程造价的预测.

RBFNN是1种3层前向网络，其网络结构如图1所示.第1层输入层由多个神经元组成，起到输入数据的作用，本文中的输入数据即约简后的多个工程特征指标；第2层隐含层包含多个径向基神经元，隐含层的作用是通过RBF激活函数将低维非线性可分的输入映射到高维线性可分的空间，隐含层输出的大小是由输入与基函数中心点的距离决定的；第3层输出层的激活函数为线性函数，最终的输出结果是隐含层神经元输出的线性加权.RBFNN的主要算法如下：

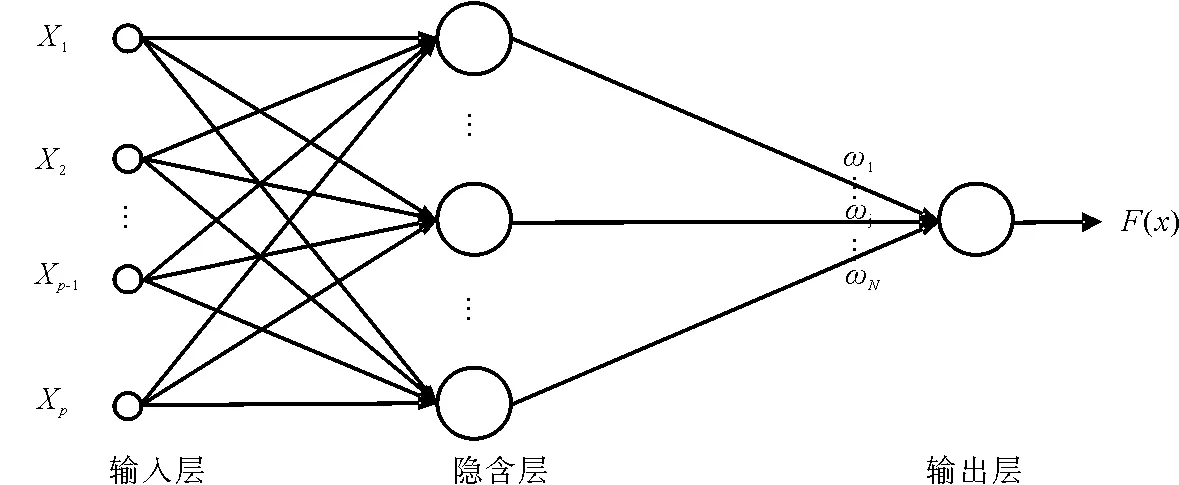
图1 RBFNN结构

对于输入的工程特征指标X=(x1,x2,…,xp)，选取隐含层的激活函数为径向基高斯函数，如式(2)所示：

(2)

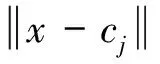
经过式(2)的非线性变换之后，便实现了从输入层到隐含层的映射.隐含层到输出层的线性映射，需要借助线性激活函数来实现，其函数公式以及权重调节公式分别如式(3)、式(4)所示：

(3)

ωij(L+1)=ωij(L)+β(Fi*d-Fi*(L))aj(x)/[aT(x)a(x)]

(4)

式中：Fi*为第i个输出量第L次计算的输出值；Fi*d为第i个输出量的期望值；a为学习率；a(x)为隐含层径向基高斯函数的映射向量.

2 工程特征指标的确定

所谓工程特征是指能表示工程特点，且能反映工程主要成本构成的重要因素.本文在参照历史工程资料的基础上，咨询专家意见，对影响工程造价的特征指标进行了全面的筛选和分析，初步确定了楼地面类型C1、基础类型C2、结构类型C3、建筑面积C4、层数C5、防水工程C6、砌筑工程C7、三级钢占比C8、门窗面积C9、门窗类型C10、内装饰C11、外装饰C12、安装工程C13这13个主要因素作为工程特征.

在所选的初始工程特征里，楼地面类型C1、基础类型C2、结构类型C3、防水工程C6、砌筑工程C7、三级钢占比C8、门窗类型C10、内装饰C11、外装饰C12、安装工程C13为分类变量，建筑面积C4、层数C5、门窗面积C9为连续变量，总造价D也是连续变量.由于利用粗糙集理论进行属性约简时，决策表中的属性值需要用离散数据表示，所以需要赋予分类变量以及连续变量相应的离散值，本文中分类变量的数据离散化见表1.

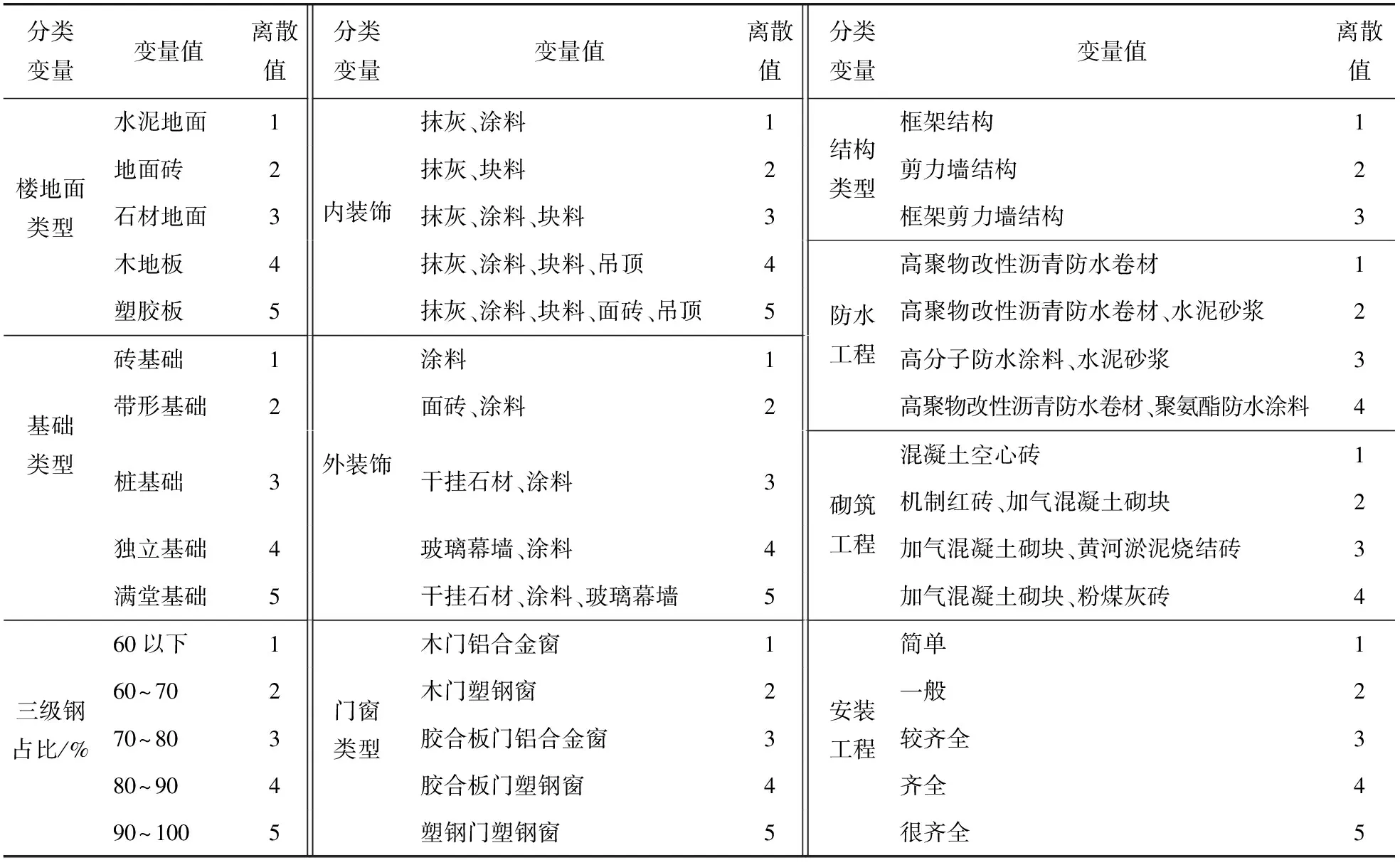
表1 分类变量离散化

3 案例分析

3.1 工程特征指标约简

本文收集了某建筑企业承建的15个类似住宅工程的样本数据，进行案例分析.首先采用粗糙集专业软件Rosetta中的Booleanreasoning algorithm离散化算法对建筑面积、层数、门窗面积、总造价这4个连续变量进行数据的离散化，然后将离散化的分类变量和连续变量形成初始决策表，选用Genetical algorithm对离散化数据进行属性约简.在运算结果中，以频次大于等于15为筛选标准，得到楼地面类型(17次)、建筑面积(30次)、门窗类型(15次)、外装饰(33次) 4个核心指标.初始决策表、初始特征约简信息表以及约简后的RBFNN输入样本数据分别见表2—4.

表2 初始决策

表3 初始特征约简信息

3.2 RBFNN预测

3.2.1 数据归一化

本文在MATLAB环境下，将粗糙集属性约简得到的楼地面类型、建筑面积、门窗类型、外墙装饰这4个指标作为网络输入，工程总造价作为网络输出，构建RBFNN模型来预测工程造价.

由于楼地面类型、建筑面积、门窗类型、外墙装饰这4个指标的数据单位不一致，它们的数据跨度也比较大，若直接输入会降低RBFNN的运行速度和预测精度.而且模型函数对输出值的范围也有所限制，所以在训练之前需要对样本数据进行归一化处理，将有量纲的表达式转化为无量纲的表达式.MATLAB环境下，样本数据的归一化需要调用premnmx函数，其命令格式为

[QN1,minQ,maxQ,RN1,mint,maxt]=

premnmx(Q,R)

其中，Q，R分别为输入矩阵和输出矩阵；minQ，maxQ分别为矩阵Q中的最小值、最大值，minR，maxR分别为矩阵R中的最小值、最大值.预测结果的输出也要进行归一化处理，这里需要调用的是反归一化函数Postmnmx，使数据分布在区间[-1，1]内.

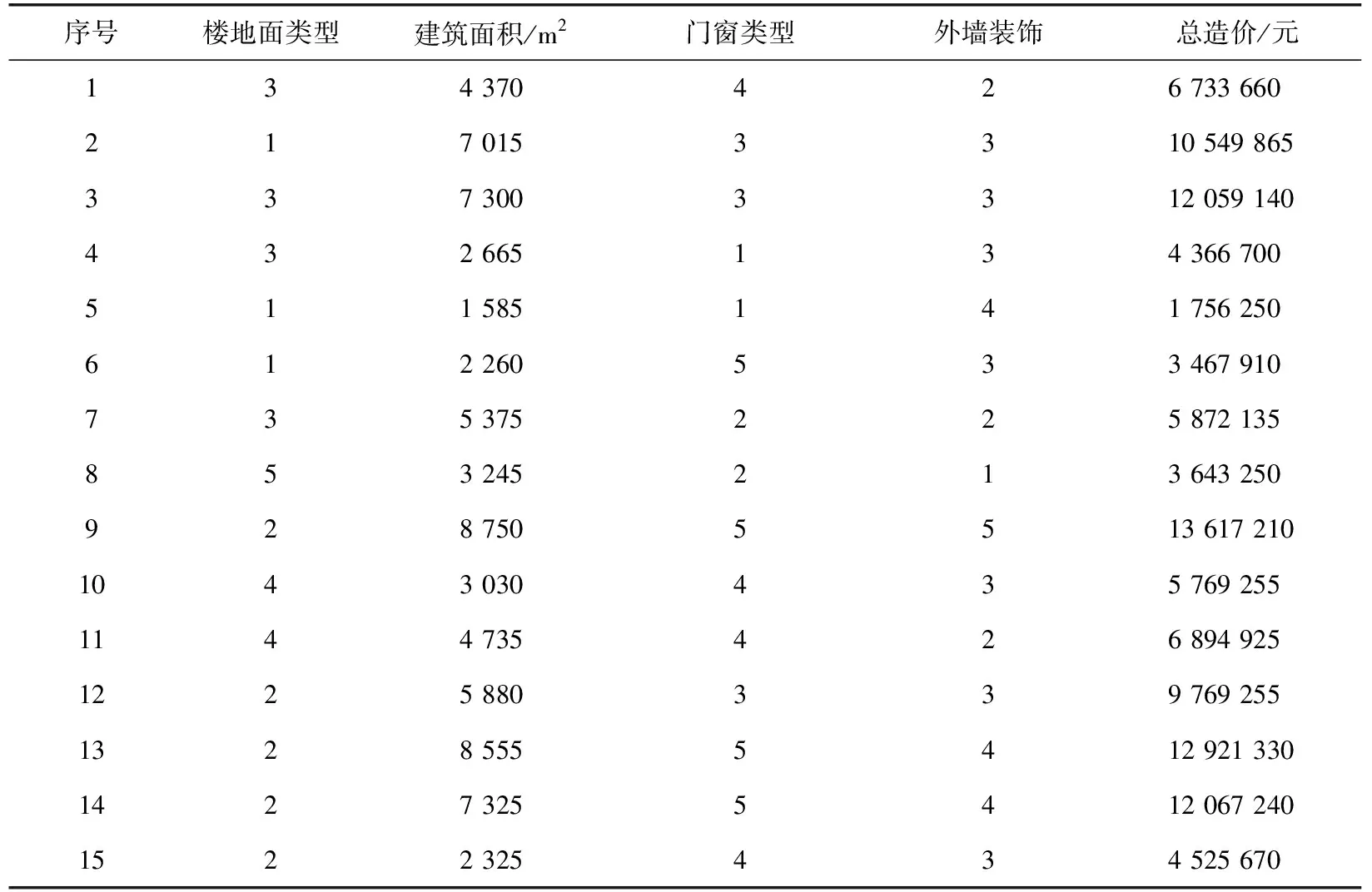
表4 RBFNN输入样本数据

3.2.2 RBFNN预测

造价数据经过归一化处理之后，即可调用RBFNN进行造价预测.RBFNN调用的命令格式为

net=newrb；

[net,tr]=newrb(QN1,RN1,mse,speed,MN,DF)

其中，QN1，RN1分别为经过归一化处理之后的输入矩阵和输出矩阵；mse为均方误差，本文将均方误差精度设为mse=0.001；speed为径向基函数的扩展速度，其值越大，网络逼近的函数就越平滑，但speed值过大或者过小，都会使模型在逼近函数时神经元增多，降低模型的预测速度，所以speed值需进行多次调试，找出最适合的值，经过多次调整，本文将speed值设为3.5；MN为最大的神经元个数，即神经元个数到了MN后立即停止网络训练，本文将MN值设为5；DF是每次加进来的网络参数，DF值设置为1.

将本文的15个样本数据分为两部分，前10个样本作为训练集，用来建立模型，后5个样本作为测试集，测试模型的性能.经过多次调试，RS-RBFNN模型的最终预测结果如图2、图3所示.

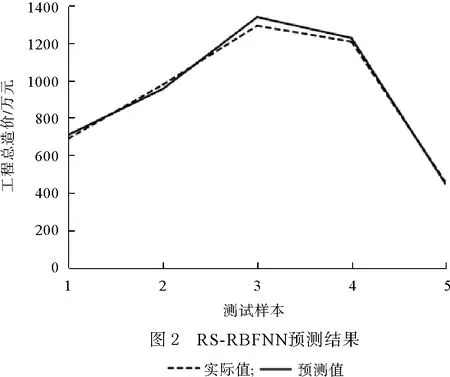
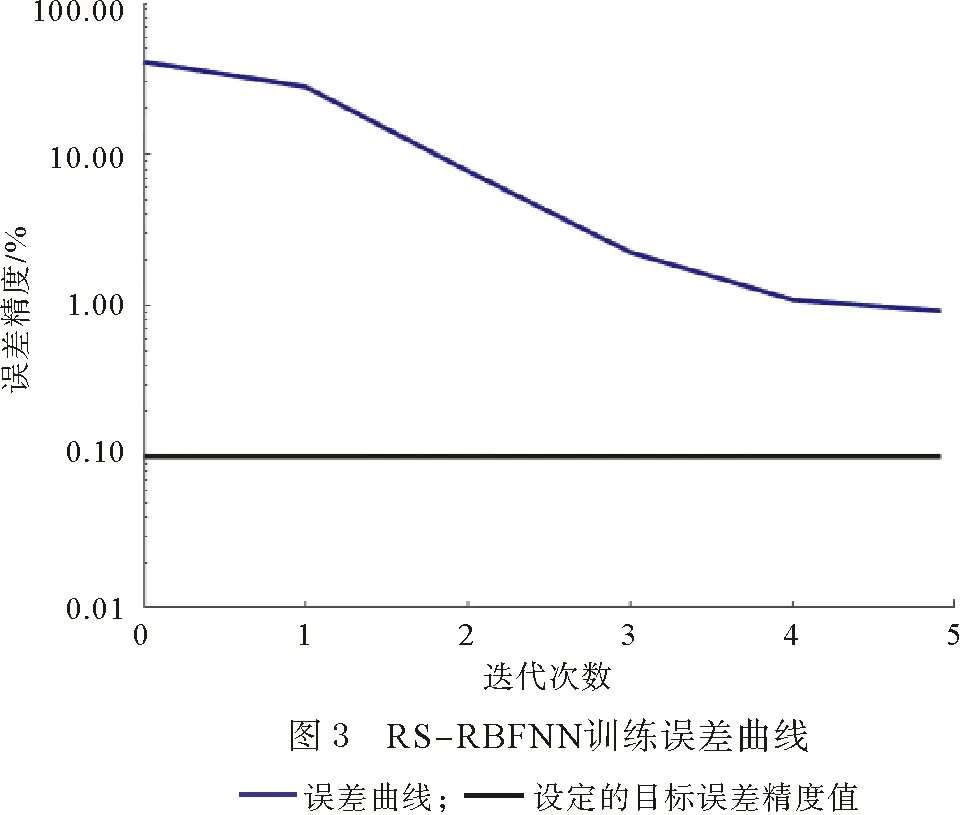
3.2.3 预测结果分析

为进一步找出RS-RBFNN模型在造价预测方面的优势，将该模型的预测结果分别与未经RS处理的BPNN、未经RS处理的RBFNN以及RS-BPNN的预测结果进行对比.

为了方便比较，选取归一化均方误差(NMSE)以及平均绝对百分比误差(MAPE)作为评价标准，误差计算公式见式(5)、式(6)：

(5)

(6)

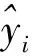
未经RS处理的BPNN、未经RS处理的RBFNN，RS-BPNN的预测结果对比见表5.

表5 不同预测模型预测结果对比

由表5可知，在预测误差方面，未经RS处理的BPNN的预测误差最大，MAPE达到18.64%，NMSE为0.205；RS-BPNN预测的误差明显减小，MAPE降低了9.81%，NMSE降低了0.148；未经RS处理的RBFNN的预测误差较小，MAPE达到9.20%，NMSE为0.061，RS-RBFNN的预测结果比上述3种模型的精度都要高，MAPE为2.46%，NMSE为0.007.在预测速度方面，RS-BPNN需要4.82 s，而RS-RBFNN只需要1.93 s，预测时间明显缩短，预测速度快.

4 结束语

1) 本文利用粗糙集的属性约简功能，从13个工程造价影响因素中，筛选出4个主要因素：楼地面类型、建筑面积、门窗类型、外墙装饰，粗糙集的属性约简很好地消除了变量间的冗余信息，简化了数据输入维数，提高了RBFNN的学习速度和预测精度，使得预测结果更加准确.

2) 将RS-RBFNN的预测结果与其他方法的预测结果进行对比，得出RS-RBFNN的预测误差和预测速度明显小于其他方法，所以RS-RBFNN模型更适合于建筑工程造价的预测.

3) 本文作为工程造价预测在智能化方向上的一次尝试性研究，以期对建筑企业提高造价管理水平有所裨益.

4) 本文提出的工程造价预测模型在预测速度、精度方面都有一定的提高，但是也存在一些不足和有待于进一步研究的地方：人工神经网络预测模型的预测精度随着样本数目的增大而提高，而本文中的样本数据是笔者通过调查搜集得到的，其数量有限，所以预测精度尚有提升空间；在目前大数据应用的背景下，今后可以考虑采用互联网集成技术，建立全面专业的数据库，以此来进一步提升造价预测的精度.