基于波纹铝板与聚氨酯泡沫的隔离自由阻尼结构振动特性研究

梁龙强，黄微波，吕 平，鞠家辉，孟凡迪

(1.青岛沙木新材料有限公司，青岛 266034；2.青岛理工大学 土木工程学院，青岛 266033)

针对现代制造业的振动问题，将阻尼材料黏附于需要减振处理的构件上，形成自由阻尼或约束阻尼结构的减振处理方式在汽车、船舰、飞机等诸多领域中得到广泛应用[1-2].在阻尼结构的基层和阻尼层之间敷设隔离层形成隔离阻尼结构，能够扩大阻尼层的耗能形变，以此来进一步提高结构的减振性能[3].燕碧娟等[4-6]研究结果表明隔离层的弹性模量是阻尼层的100倍时，管状隔离阻尼模型能够达到更好的减振效果.SANJIV[7]认为增大约束层的厚度和模量能够改善隔离型约束阻尼结构的减振性能.易少强等[8-9]利用ANSYS和MATLAB协同仿真的方法，证明了粒子群算法能较好地解决隔离阻尼结构的动力学优化问题.石慧荣等[10-11]对局部敷设隔离层的约束阻尼结构进行了分析，认为局部隔离阻尼处理虽然使得阻尼面积减小，但其阻尼效率更高.RAO，ZHAO等[12-15]研究结果表明带槽隔离层的引入对结构阻尼性能的提升起到了很好的促进作用.

目前针对隔离型约束阻尼的研究已经比较深入，而对隔离型自由阻尼结构的研究相对较少[16-20].本文以钢板作为基层，橡胶材料作为阻尼层，并以波纹铝板和聚氨酯泡沫作为隔离层制备成悬臂梁模型，通过单点锤击实验，从时域波形、传递函数曲线、模态频率及损耗因子等方面分析隔离自由阻尼悬臂梁的阻尼性能.

1 实验部分

1.1 模型设计与制备

隔离自由阻尼悬臂梁模型主要由基层、隔离层和阻尼层三部分构成.模型基材采用市面所售的Q235钢板，密度为7800 kg/m3，弹性模量为210 GPa.隔离层中波纹铝板由浙江嘉善强飞蜂窝机械设备有限公司采用型号为3003H18号铝生产(图1)，铝板厚度为0.21 mm，波纹铝板密度为2710 kg/m3；聚氨酯泡沫由青岛永德聚氨酯有限公司提供，密度为160 kg/m3，弹性模量为130 MPa.阻尼层采用天津橡胶工业研究所提供的D-803-ZR橡胶阻尼材料，密度为1450 kg/m3，弹性模量为45 MPa；层间黏结剂采用青岛沙木新材料有限公司提供的Qtech-413胶黏剂，以此制备实验用隔离阻尼自由结构悬臂梁模型.

图1 波纹铝板隔离层

将黏结剂Qtech-413的A，B组分按比例1.1∶1混合后搅拌均匀，分别刮涂于除锈后的钢板和阻尼橡胶表面，厚度为0.5 mm.将波纹铝板和聚氨酯泡沫分别放置在涂有胶黏剂的钢板上，再将橡胶阻尼材料涂有胶黏剂的一侧扣压在隔离层之上.将制备完成的悬臂梁模型放于夹具中固定，防止滑移，并在25～30 ℃，相对湿度为54%～58%的条件下养护7 d，然后进行测试.隔离自由阻尼悬臂梁模型结构如图2所示，垫高层材料及尺寸参数见表1.

图2 悬臂梁模型结构

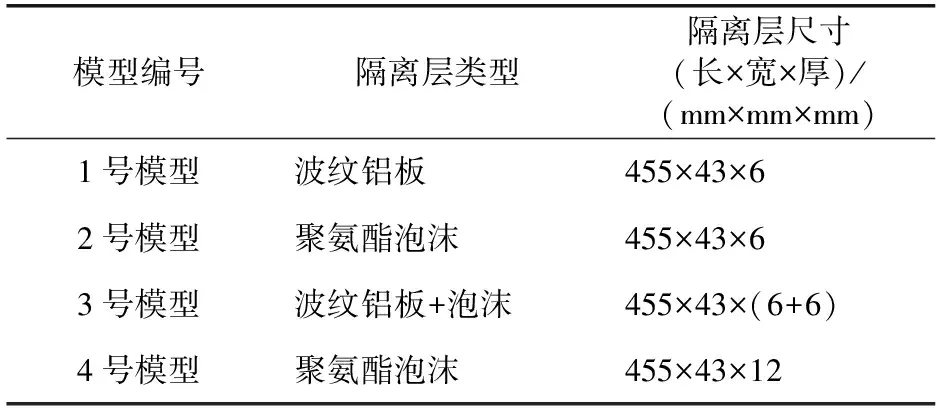
表1 悬臂梁垫高层材料及尺寸参数

1.2 实验设备与方案

实验测试分析系统包括激励力锤、支撑组件、传感器、信号采集仪和控制分析系统，如图3所示.信号采集仪采用北京东方振动和噪声技术研究所研发的INV3062T0采集仪；分析软件为DASP-V11工程版；激励力锤采用INV9313型ICP力锤，灵敏度为0.201 mV/N；传感器采用朗斯测试技术有限公司LC0103型ICP加速度传感器，灵敏度为50 mV/g.

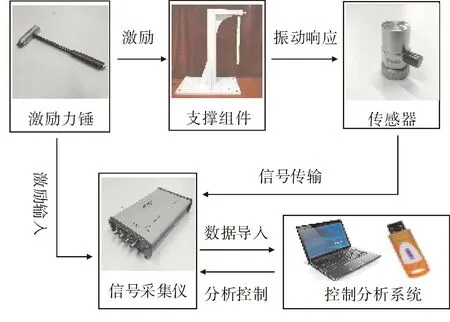
图3 测试分析系统

测试方法采用悬臂梁单点锤击法，锤击点和拾振点分别布置在距固定端和自由端25 mm中点处，锤击力为60 N；测试的采样频率为51.2 kHz，变时倍数为8，触发次数为3次，采样点数为16 384个.测试时实验室温度为23 ℃，相对湿度为56%.

2 实验结果与分析

2.1 时域分析

对传感器采集到的加速度衰减信号进行时域分析，得到1—4号模型的时域波形，如图4所示.

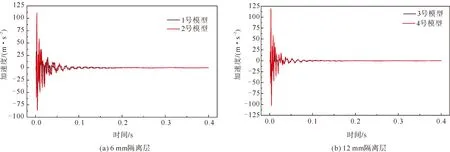
图4 不同隔离层厚度的悬臂梁振动波形

由图4(a)可知，1号和2号模型加速度最大振幅分别为105和111 m/s2.相比于2号模型，1号模型最大振幅降低了5.41%，而且衰减时间明显减少，所以波纹铝板作为隔离层的减振效果要优于聚氨酯泡沫材料.这可能是因为相比于聚氨酯泡沫材料，波纹铝板更接近理想的垫高层模型，即剪切刚度极大而抗弯刚度极小[19-20]，有利于发挥垫高层杠杆放大作用，基层的弯曲形变向阻尼层的传递效率更高，所以提高了结构整体的减振效果.由图4(b)可知，3号和4号模型加速度最大振幅分别为74和119 m/s2.相比于4号模型，3号模型最大振幅降低了37.82%.在0.2 s时，3号模型已几乎完全平缓，而4号模型依旧保持着0.39 m/s2振动幅度.

对比图4(a)和(b)可知，与隔离层厚度为6 mm的阻尼结构相比，隔离层厚度为12 mm的结构持续振动时间较短.这表明，垫高层厚度增加之后，悬臂梁模型的减振效果更加明显.这是因为外部橡胶阻尼层的中性轴至悬臂梁中性轴的距离p为[19]

(1)

即

(2)

式中：hb，hs和hv分别为基层、垫高层和阻尼层的厚度；Eb，Es和Ev分别为基层、垫高层和阻尼层的弹性模量；d1和d2分别为垫高层和阻尼层的中性轴到基层中性轴的距离.

由式(2)可知，随着hs的增加，阻尼层处理距离p相继增大，这相当于加大了阻尼层的厚度.因此，在基层形变相同时，外部橡胶阻尼层的形变随之增加，由此引起分子链段的相对滑移增大，阻尼层耗能增多，悬臂梁的减振性能因此提升.

2.2 传递函数曲线

1—4号模型的传递函数曲线如图5所示.

图5 不同隔离层厚度的悬臂梁传递函数曲线

由图5(a)可以看出，在前三阶，1号模型(单一波纹铝板的隔离自由阻尼结构)模态振动峰值要明显低于2号模型，两种结构在第四阶的模态振动峰值相差不大，分别为6.3和6.7 m·s-2/N.由图5(b)可以看出，3号模型一阶到四阶的模态振动峰值分别为3.49，3.62，4.46和4.91 m·s-2/N.相对于4号模型，3号模型在各阶模态振动峰值都有明显的降低，各阶分别降低了29.21%，53.39%，53.44%和36.65%.

四种阻尼结构中，2号和4号模型这两种隔离层为聚氨酯泡沫的阻尼结构在单位力下的振动加速度响应十分剧烈，而3号模型的模态振动峰值降低最为显著，其次是1号模型.这说明采用波纹铝板作为隔离层能够有效地降低悬臂梁模型的振动加速度响应，提升结构的阻尼性能，这与前述时域波形分析结果相吻合.

2.3 损耗因子及模态频率

通过对振动加速度谱图进行分析并采用半功率带宽法进行计算，得到各阶的模态频率和损耗因子，计算结果见表2.

表2 模态频率及损耗因子

由表2可知，1号模型的损耗因子略高于2号模型，一阶到四阶的损耗因子分别增加了0.0012，0.0092，0.0037和0.0039，1号模型阻尼效果更优.随着隔离层厚度的增加，3号和4号模型的损耗因子相对于1号和2号模型有了明显的提升，每一阶提升了20%～40%.相对于4号模型，3号模型的一阶到四阶损耗因子依次增加了0.0353，0.0117，0.0178和0.0009，减振性能有所提升，与前述分析结果相一致.

同时，可以发现随着隔离层厚度的增加，各阶模态频率统一向高频方向移动.在一阶模态峰处，3号和4号模型在各阶的模态频率保持一致，模态频率比1号和2号模型提升了7.35%.在二阶、三阶和四阶，3号和4号模型对于2号模型有3%～8%的提升.这是因为随着隔离层厚度的增加，结构的刚度、质量均随之增加，但刚度增加的比例较大，因此频率也随之上升.

3 结论

1) 四种结构中，隔离层为12 mm的两种阻尼结构与隔离层为6 mm的结构相比，阻尼减振性能整体上有很大提升，具体表现在波形衰减时间减少了0.1 s，损耗因子提高20%～40%.

2) 隔离层为6 mm波纹铝板与6 mm聚氨酯泡沫的组合结构在各频段表现出良好的减振效果，单位力下的振动响应最小，峰值范围仅为3.49 ～4.91 m·s-2/N，并且损耗因子的提升显著.隔离层为6 mm的波纹铝板阻尼结构在降低单位力下振动响应和波形衰减时间方面表现出较好的减振性能.

3) 两种隔离层为聚氨酯泡沫的结构，厚度为6 mm的结构减振性能最差，振动响应最高，损耗因子最小；厚度为12 mm的结构衰减时间少，且损耗因子更高.