矩形板受分布荷载作用下的解析解

李壮飞，寇子琦，刘 海，侯钢领，王滨生，*

(1. 哈尔滨工程大学 土木工程系，哈尔滨 150001；2. 中核四〇四有限公司 第二分公司，兰州 732850)

弹性板在工程中使用非常广泛，尤其是弹性薄板更为普遍.其中三边固支一边自由的矩形板广泛应用于航空、船舶、核电、水利工程中，如土木工程的挡土墙、核安全壳屏蔽结构[1]等均可视为具有该边界条件的板.因此，一种精确且简单的板弯曲解决方案具有显著的实际意义.

本文依托我国某石墨慢化沸水堆承重水箱实际工程项目，研究核设施的安全特性和风险评估.为研究反应堆内承重水箱的最弱失效位置，通过刚度等效和厚度等效建立了该水箱的简化模型.一般矩形容器问题通常转化为三边固支一边自由的板壳问题来解决，分析矩形板的各种受力工况，本研究的关键点和难点在于：矩形板侧面承受分布线荷载的求解.工程简介如图1所示.关于矩形板弯曲问题，大多数研究都是应用边界条件简化板边约束，这需要沿边线对其一阶导数或二阶导数进行偏转.然而当载荷和边界条件过于复杂且无法用函数式表示时，这会导致基本挠度方程无法适用，甚至难以求解.对矩形薄板弯曲问题，可以从对边简支板的Navier解出发，利用双三角级数方法解决[2].对于一般边界的矩形薄板通常采用叠加法或补充项的方法解决[3-5].针对其他边界类型的板采用复变函数法、有限积分法、辛弹性力学法.如ULLAH等[6]引入双重有限积分变换方法，探讨了带有角支撑的矩形薄板的解析弯曲解，给出了特定边界条件下板弯曲的一般精确解析解.LI等[7]采用辛叠加法研究了三个角点支撑的矩形薄板弯曲问题.SHI等[8]通过叠加经典的Navier和Levy解，研究了在集中力作用下具有旋转约束边缘的矩形板的弯曲问题.ZHANG等[9]通过广义积分变换将高阶偏微分方程简化为线性代数方程的方法探索了组合薄板在简单简支、固支和自由边界条件下的弯曲解析解.

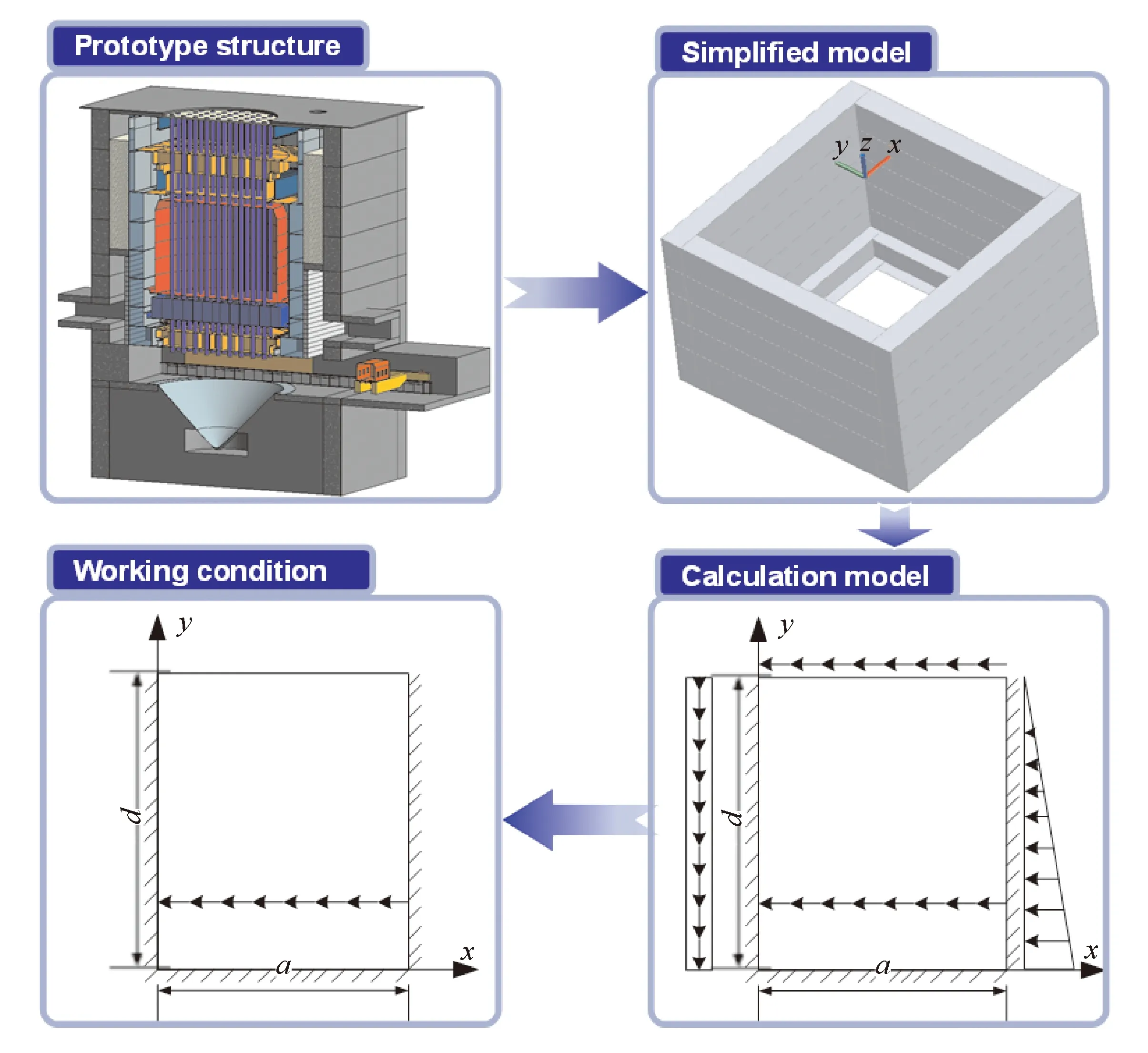
图1 工程简介

值得注意的是，上述研究缺乏矩形板在侧面分布线荷载作用时的实际工程研究.目前关于核安全壳工程项目中板类计算的实际应用研究相对较少.因此，本文依托我国某石墨慢化沸水反应堆的承重水箱实际工程项目，通过结构简化，分离出此种矩形板受力工况，以三边固支一边自由矩形板受侧面分布线荷载作用下的弯曲作为研究内容，依据Kirchhoff薄板理论，采用双向三角级数来表示挠度函数，把复杂板面分布荷载转化为经典矩形板的边界条件，然后求解满足边界条件的线性方程组建立了基于静态的薄板在分布线荷载作用下的弯曲分析模型.本解法与经典Levy解的原理一致，并克服了经典Levy针对板面荷载过于复杂时无法用解析式表达的局限性.

1 基本方程和边界条件

矩形板的边长分别为a和d，边界条件为三边固支一边自由.当板侧面作用法向载荷q(x,y)时，基本微分方程：

(1)

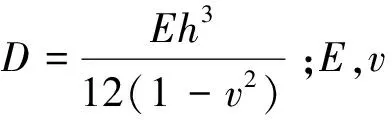
设方程(1)解的形式为

w(x,y)=w*(x,y)+w0(x,y)

式中：w*(x,y)为方程(1)的非齐次方程特解；w0(x,y)为方程(1)的齐次方程的通解.

图2所示矩形板，y=d为自由边界，其余三边固支，沿y=c的直线OO′上分布有线荷载V0(x)和M0(x)，其中线荷载V0(x)是竖直性质的荷载；M0(x)为力矩性质的荷载，它们的正方向如图2所示.

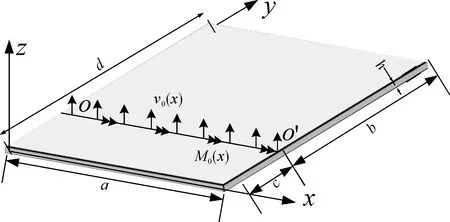
图2 矩形板结构

为方便叙述，下文内容凡提到w，w1，w2时，无特殊说明，均代表含有x，y的二元函数.设图2中矩形板的挠度为w，显然它并不能用一个连续的函数来表示，设位于0≤y≤c的区域上，矩形板的挠度表达式为w1，位于c≤y≤d的区域上，板的挠度为w2，则w1和w2分别满足以下2个方程：

▽2▽2w1=0, 0≤y≤c

▽2▽2w2=0,c≤y≤d

同时也要满足12个边界条件，即沿薄板周边的8个和沿OO′线上的4个，分别为

x=0边上：

x=a边上：

y=0边上：

y=d自由边上：

沿OO′线必须满足4个边界条件：

w1(x,c)=w2(x,0)

Vy1-Vy2=V0(x)

M1-M2=M0(x)

2 边界条件下的基本微分方程的解

为表示板的双向弯曲变形，设通解中w1和w2的表达式是各包含8个待定常数的双向三角级数，图3表示了[0，c]区间上矩形板的荷载和边界情况，图4表示了[c，d]区间上矩形板的荷载和边界情况.其中w2的y坐标零点设在整块板的y=c处.

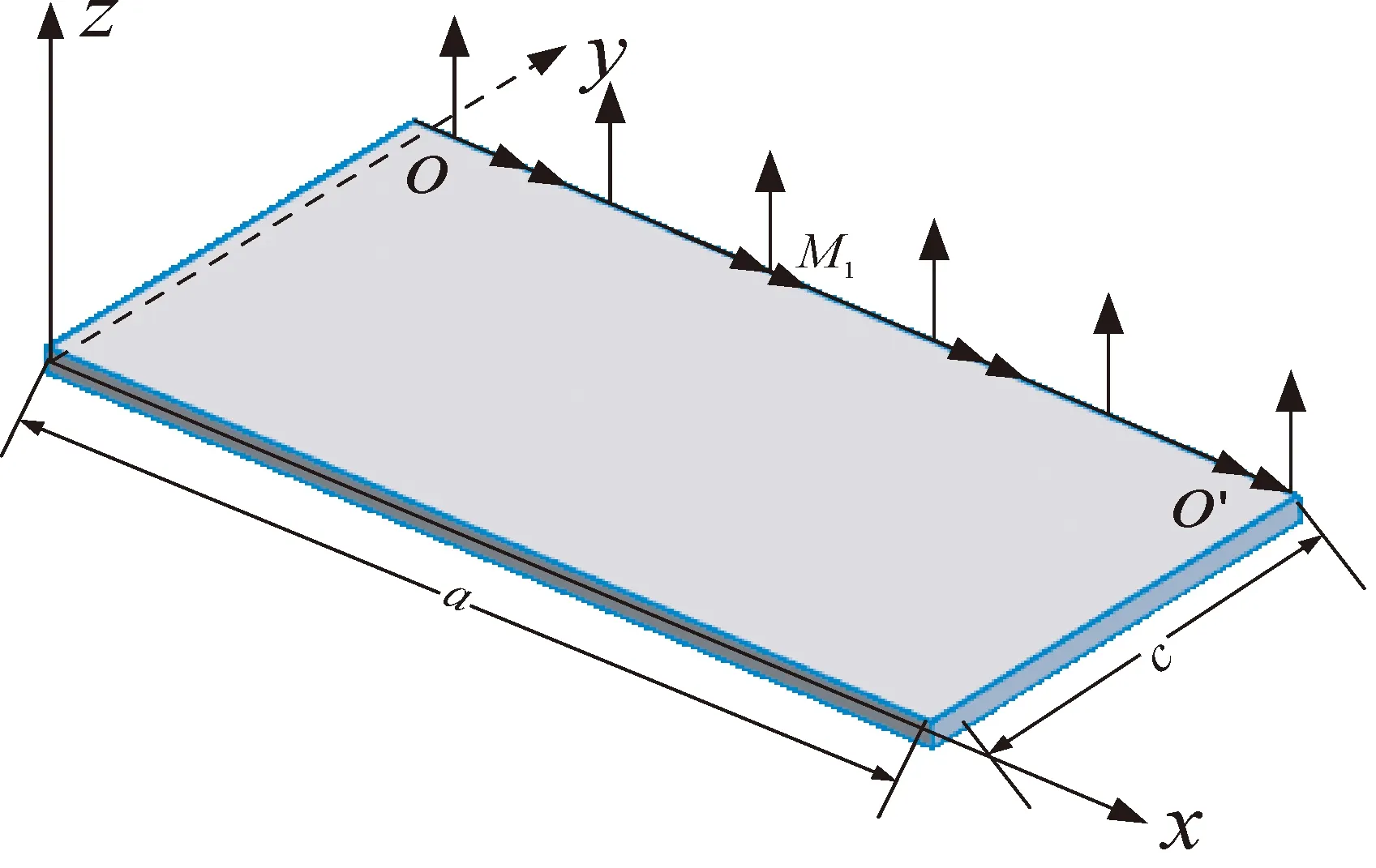
图3 [0,c]区间荷载

图4 [c,d]区间荷载

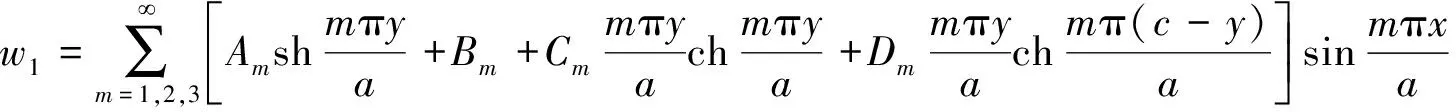
(2)

(3)

式中：Am，Bm，Cm，Dm，En，Fn，Gn，Hn，Im，Jm，Km，Lm，Mn，Nn，On，Pn为16个待定常数.

w1的三边边界条件所对应的线性方程组见表1.

表1 w1(x,y)边界条件对应的方程式

w2的三边边界条件所对应的线性方程组见表2.

表2 w2(x,y)边界条件对应的方程式

沿OO′线需满足4个边界条件，相对应的方程组如表3所示.

表3 OO′线边界条件对应的方程式

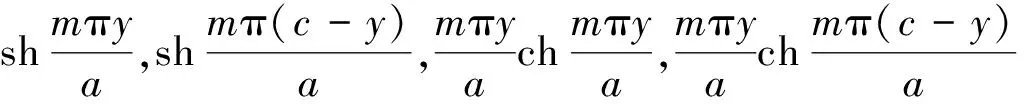
将挠度函数表达式式(2)、式(3)中的第1个级数和第2个级数均取前N项时，联立表1—3中16个方程，可得到16×N阶线性方程组.该方程组可采用高斯消元法解得16×N个待定常数.将求得的待定常数代入到挠度函数式，至此求得矩形板在侧面沿线荷载作用下的挠度函数.由挠度函数表达式便可进一步得到板中每一点的挠度值、弯矩值和应力应变值.随着N项的增大，计算精度会得到显著的提高.

3 算例与精度检验

3.1 算例

如图5所示，矩形板由钢材制作而成，尺寸为l1×l2×h=18 m×15 m×0.4 m.材料密度取ρ=7850 kg/m3，泊松比取v=0.3，弹性模量E=2.06×1011Pa.边界条件为三边固支一边自由，其中在y=15边线处自由；在y=3处，承受均匀分布的弯矩M0(单位长度弯矩值为M0)作用，均匀弯矩M0=5×107N·m.计算该矩形板静力响应.

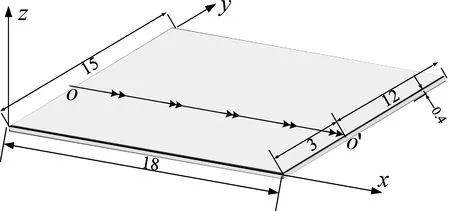
图5 结构与荷载

依据上述推导过程，采用Visual Fortran95语言编制程序，给出了相关挠度、应力分量计算结果，见图6.

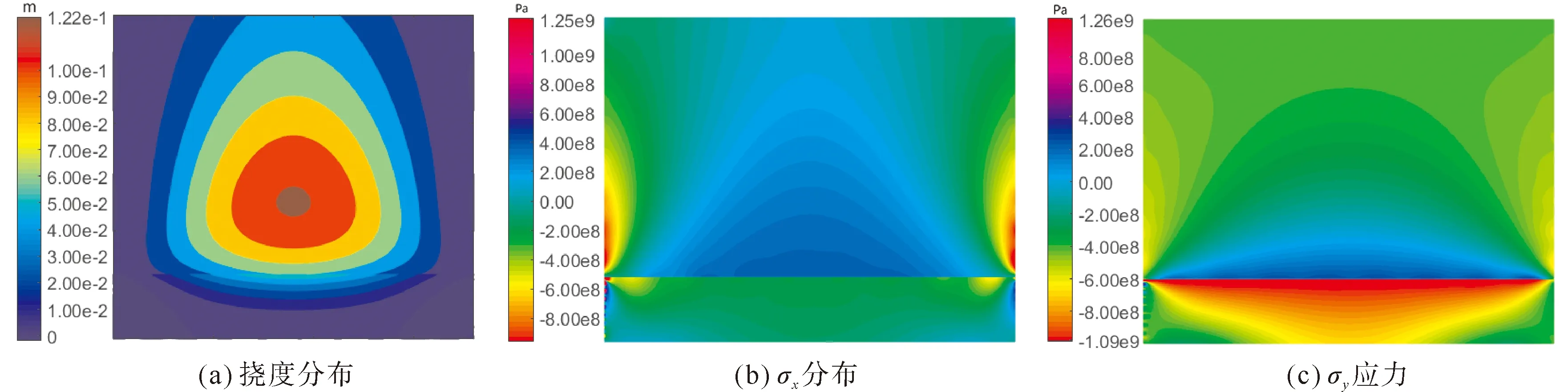
图6 本方法计算结果

3.2 精度检验

为了验证上述力学模型的正确性，进一步利用有限元ANSYS.WORKBENCH18.0软件计算分析.首先，在矩形板上选取5个坐标点，分别为P1(9 m,1 m)，P2(9 m,3 m)，P3(9 m,5 m)，P4(9 m,12 m)，P5(9 m,15 m).统计每个坐标点的响应值，相应的精度误差Eri定义为

其中，上标ref是有限元计算结果.

此外，图8中显示了有限元模型与本文方法取前16项时挠度计算结果之间的差异.显然，本方法获得的挠度响应分布与有限元模型结果非常吻合.

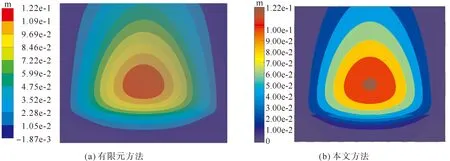
图8 挠度响应分布对比

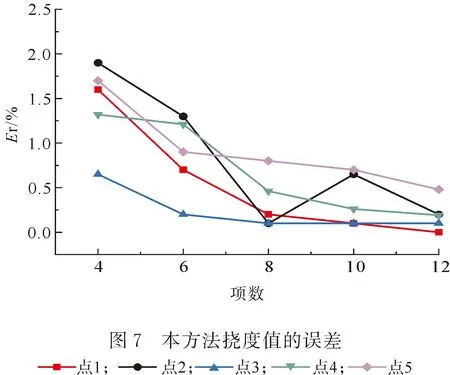
接着，研究5个坐标点的弯矩响应.图9表示取不同项数时本方法5个响应点弯矩值的误差.随所取项数的增加，计算值与有限元值的计算误差逐渐减小.每个点的收敛速度均较快，且取到前6项时每点的弯矩响应误差均控制在4%以内，当项数增加到前8项时，误差已达到3%以内.表明本方法在计算矩形薄板弯矩响应时收敛速度快，计算精度高.

最后，研究矩形板上的应力极值响应.如图10所示，与有限元值对比，可以看出，随所取项数的增加，计算值与有限元值两者逐渐逼近.当本方法取到前20项时，与有限元模型计算结果相当吻合.

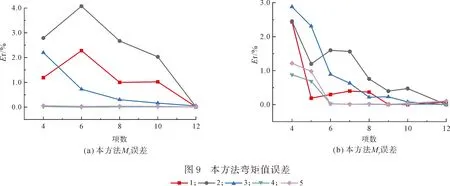
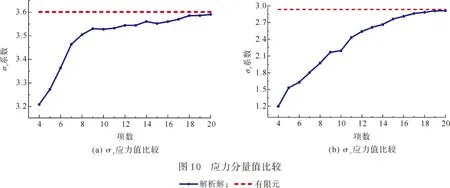
图11、图12分别列出了该矩形板的应力响应分布.结果表明，本方法获得的应力分量响应分布与有限元计算结果非常吻合.

图11 σx应力分布对比

图12 σy应力分布对比

4 结论

针对实际核安全壳工程项目中的平板类计算问题，本文给出一种求解矩形板侧面沿线分布均匀荷载时弯曲问题的方法.该方法确定了矩形板侧面沿直线承受分布荷载时的挠度和内力计算表达式，应用分段面处函数的连续性和突变性，把板面分布荷载转化为经典板边界条件，然后选择特定的特征函数，建立了基于静态的薄板在均匀线荷载下的弯曲分析模型，给出了线分布荷载作用下三边固支一边自由矩形薄板的数值解.对于相同边界条件下，当板面受到不同形式的线分布荷载时，只需改变线性方程组等号右端控制方程即可求得问题的解.分析结果表明，该计算方法具有收敛速度快、计算精度高、物理意义明确等优点.随所取待定系数项数的增加，计算精度可以取得令人满意的结果.本研究对实际核安全壳受复杂载荷的工程问题具有一定的参考价值.