基于0-1规划的最小属性约简算法

詹婉荣，于 海

(洛阳师范学院 数学科学学院, 河南 洛阳 471934)

粗糙集理论是波兰数学家Pawlak于1982年提出的，它是一种新型的处理模糊和不确定知识的数学工具，其主要思想就是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则[1]. 属性约简是粗糙集理论中的核心内容之一.数据库中的属性并不是同等重要的, 甚至其中某些知识是冗余的，通过属性约简, 可以去除数据库中的冗余、无用的成分, 揭示数据中隐含的规律.从粗糙集理论的角度来理解, 在一个信息系统中, 有些属性对于分类来说是多余的, 去掉这些属性后，信息系统的分类能力不会改变, 所以属性约简后仍然反映了一个信息系统的本质信息[2-6].一般来讲，一个信息系统的属性约简不是唯一的，通常人们希望能够找到一个属性个数最小的属性约简，该属性约简称为最小属性约简.对任一给定信息系统，若属性约简算法能确保找到其最小属性约简，则该算法称为最小属性约简的完备算法.

然而，Wong和Zlarko已经证明了寻找一个信息系统的最小约简是NP-hard 问题[7].导致NP-hard 问题的主要原因是属性的组合爆炸问题.传统的属性约简算法大都属于启发式的搜索算法，它们的优点是易于实现，且计算速度快，但求出的不一定是最小属性约简.因此在本文中，我们将最小属性约简问题转化为一个优化问题，进而转化为0-1规划.通过求解该0-1规划，得到了信息系统的最小属性约简.在此基础上给出了基于0-1规划的最小属性约简算法，并且该算法是最小属性约简的完备算法.

1 信息系统及其属性约简

本小节仅介绍与本文有关的主要概念，其他概念可参见文献[8-9].

定义1信息系统S是一个四元组：S=(U,AT,V,f)，其中U表示对象的非空有限集合，称为论域；AT表示属性的非空有限集合；V是属性的值域集；f是信息函数，f:U×AT→V.

定义2设A⊆AT，不可区分关系ind(A)⊆U×U定义如下

ind(A)={(x,y)∈U×U|∀a∈A,

f(x,a)=f(y,a)}.

对任意两个对象x,y∈U，若xind(A)y，则基于属性集A，x和y是不可区分的.

根据不可区分关系的定义，Pawlak将信息系统的约简定义为保持不可区分关系ind(AT)不变的极小属性集.

定义3设S=(U,AT,V,f)为一信息系统，属性集R⊆AT称为一个约简，如果满足以下两个条件：

(1)ind(R)=ind(AT)；

(2) ∀a∈R，ind(R-{a})≠ind(AT).

一般情况下，信息系统的约简不唯一，所有约简之集记作Red(S).

定义4所有约简的交集称为核，记作Core(S).

设S=(U,AT,V,f)为信息系统，其中

U={u1,u2, …,un}，AT={a1,a2, …,am}.

定义5设S=(U,AT,V,f)为信息系统，|U|=n，S的区分矩阵是一个n×n的矩阵M=(Mij)，其中Mij对应对象(ui,uj)，定义为

Mij={a∈AT|f(ui,a)≠f(uj,a)}.

Mij是由能区分对象ui和uj的属性组成的集合.如果Mij≠φ，那么对象ui和uj是可区分的.另外，区分矩阵M是对称的，即Mij=Mji，且Mii=φ.所以，只需给出区分矩阵的下三角矩阵即可.

定义6区分矩阵M的区分函数定义为

f(M)=∧{∨Mij|Mij≠φ, 1≤i,j≤n}.

其中∨Mij表示Mij中的属性的析取，∧{∨Mij}表示∨Mij的合取.

2 基于0-1规划的最小属性约简算法

虽然利用定义6中的区分函数可以求出所有的约简，但在实际应用中，有时只需找到一个约简即可.于是人们去寻找最小约简(即约简中属性的个数最小).

在给出基于0-1规划的最小约简算法之前，我们先分析约简产生的过程.

定理1设S=(U,AT,V,f)是一个信息系统，M为S的区分矩阵，R⊆AT为S的一个约简当且仅当以下两个条件成立.

(1) ∀1≤i,j≤n，Mij≠φ⟹R∩Mij≠φ;

(2) ∀a∈R, ∃i,j, 使得Mij≠φ，满足

(R-{a})∩Mij=φ.

由定理1可知，一个约简和区分矩阵中每个非空元素的交都不能为空.也就是说，约简中的属性取自区分矩阵中这些非空元素，但是这些元素之间存在“重复”现象.

定义7设X,Y为区分矩阵M中的2个元素，若X⊆Y，即X中的属性都是Y中的属性，称Y为X的重复元素.

为了容易求得约简，我们把区分矩阵中的重复元素删去，同时也去掉空集，引入极小区分集的概念.

定义8设MS={S1,S2, …,Sl}满足以下条件:

(1) ∀Sk∈MS，存在区分矩阵元素Mij，使得

Mij≠φ，Sk=Mij;

(2) ∀i,j∈{1, 2, …,n}，

k∈{1, 2, …,l}，Mij≠φ，

若Mij⊆Sk，则Sk=Mij.

则称MS为信息系统S=(U,AT,V,f)的极小区分集.

由定义8可知，极小区分集实际上是由区分矩阵中非空元素的极小元组成的.换句话说，在区分矩阵中，删去所有重复元素和空集就得到了极小区分集.

在得到约简的过程中，极小区分集与区分矩阵起到相同的作用，可以代替区分矩阵.

定理2设MS为信息系统S的极小区分集，

R⊆AT，则R为一个约简的充要条件是：

(1)R∩Si≠φ，i=1, 2, …,l；

(2) ∀a∈R, ∃k∈{1, 2, …,l}，

(R-{a})∩Sk=φ.

证明由定理1和定义8容易得证.

由定理2，可将计算最小属性约简R转化为如下的优化问题：

min|R|

(1)

s.t.R∩Si≠φ，i=1, 2, …,l，

∀a∈R, ∃k∈{1, 2, …,l},

(R-{a})∩Sk=φ,

其中|R|表示R中属性的个数.

经过分析，可将上述的优化问题的第二个条件去掉，得到如下定理.

定理3R为信息系统S的最小属性约简当且仅当R为下面的优化问题的最优解.

min|R|

(2)

s.t.R∩Si≠φ，i=1, 2, …,l.

证明只需证明优化问题(2)和优化问题(1)等价.

(ⅰ)设R*为(2)的最优解，为了证明R*为(1)的最优解，只需证明R*满足∀a∈R*, ∃k∈{1, 2, …,l}，(R*-{a})∩Sk=φ即可.

用反证法，假设∀a∈R*, ∃k∈{1, 2, …,l}，(R*-{a})∩Sk=φ不成立，其等价于∃a∈R*,

∀k∈{1, 2, …,l}，(R*-{a})∩Sk≠φ.令R′=R*-{a}，则∀i∈{1, 2, …,l}，

(R′)∩Si≠φ，R′为(2)的可行解.

但|R′|<|R*|，这与R*为(2)的最优解相矛盾.因此R*满足∀a∈R*, ∃k∈{1, 2, …,l}，(R*-{a})∩Sk=φ，即证R*为(1)的最优解.

(ⅱ)反过来，设R*为(1)的最优解，易知R*为(2)的可行解.又因为R*满足条件∀a∈R*, ∃k∈{1, 2, …,l}, (R*-{a})∩Sk=φ，则R*去掉任意一个属性，(2)的约束条件就不再成立，由此说明R*为(2)的最优解.

下面将优化问题(2)转化为0-1规划.

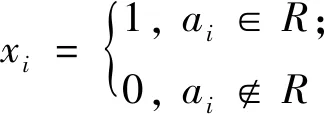
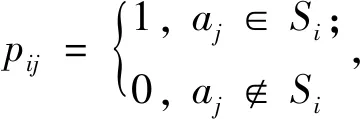
j=1, 2, …,m.同样容易验证

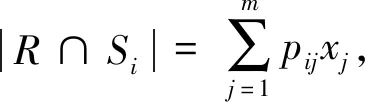
(3)

xj=0或1.

以下将0-1规划(3)改写为矩阵形式.

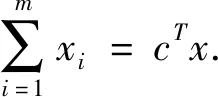
mincTx

(4)

s.t.Px≥q

xj=0或1.

由定理3可知，计算信息系统的最小属性约简可转化为求解0-1规划(4).而解决0-1规划问题通常采用隐枚举法，隐枚举法只需比较目标函数在一小部分组合点上的取值大小就能求得最优解，从而大大减少了工作量.而且0-1规划是常见的优化方法，在生产、生活中有着广泛的应用.目前常见的数学软件如MATLAB、LINGO等均能直接求解.

本文将计算信息系统的最小属性约简转化为求解0-1规划问题，求得的约简必定是最小属性约简，所以本文中提出的基于0-1规划的最小属性约简算法是完备的.

接下来我们给出基于0-1规划的最小属性约简算法.

步骤1 由定义5求区分矩阵M；

步骤2 计算极小区分集MS={S1,S2, …,Sl}；

步骤3 由极小区分集MS计算矩阵P=(pij)，其中

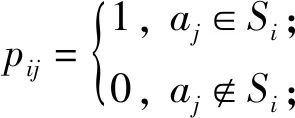
步骤4 求解0-1规划(4) ，得到一个最小属性约简.

3 实例分析

为了进一步说明本文提出的基于0-1规划的最小属性约简算法，下面给出一个实例.

例1 给定一个信息系统如表1所示，其中U={x1,x2, …,x8}为对象集，AT={a1,a2, …,a6}为属性集.下面给出求表1所示信息系统的最小属性约简的过程.

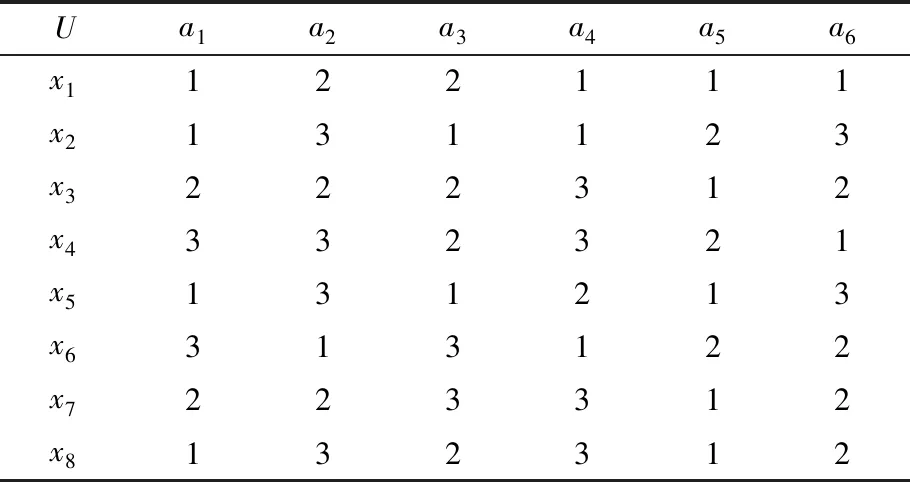
表1 信息系统

为了方便，我们将属性a1,a2, …,a6分别用1, 2, …, 6表示. 按照定义5计算得到信息系统的区分矩阵M为

MS={{1, 4, 6}, {2, 4, 6}, {4, 5}, {3}, {1, 2}, {1, 5, 6}}.

计算得到矩阵P为

计算0-1规划

mincTx

s.t.Px≥q

xj=0或1.

得到最优解为x=(1, 0, 1, 1, 0, 0)T，于是信息系统的最小属性约简为R={a1,a3,a4}.

4 结语

属性约简是粗糙集理论的核心内容之一.由于寻找信息系统的所有约简是NP完全问题，因此本文研究了信息系统的最小属性约简问题. 将最小属性约简问题转化为0-1规划问题，从而提出了基于0-1规划的最小属性约简算法.本文中的属性约简方法为粗糙集的属性约简提供了新的方法.实例分析表明，本文的算法是有效可行的.