平行分度凸轮传动机构CAD/CAM系统与运动仿真

黄立靖

(福建林业职业技术学院 自动化工程系，福建 南平 353000)

随着科学技术的发展与应用需求的增加，对凸轮传动机构的性能要求也在不断提升. 平行分度凸轮相较于其他传统凸轮机构来说，具有分度精度高、动力性能好等优点，更能适应现代化生产与发展的需要，现已被广泛应用于工程机械与食品加工等多个领域[1]. 各方面的研究受到学者们的密切关注，葛正浩等构建了平行分度凸轮机构CAD/CAM设计系统，并对凸轮机构进行了运动仿真[2]； 赵浩东等结合刚柔耦合理论与凸轮机构的特点构建了动力模型，并对平行分度凸轮机构进行了动态仿真[3]； 高英等通过一种曲线轮廓构造新方法来设计平行分度凸轮机构系统，实证分析结果显示，该系统满足实际工程的特殊需要，同时具有良好的通用性能[4]. 鉴于平行分度凸轮机构应用的特殊性，开发一款实用性、专业性强的CAD/CAM设计系统显得非常重要.

1 平行分度凸轮基本理论

1.1 平行分度凸轮机构运动机理

平行分度凸轮能够将输入轴的连续转动转化为输出轴的间歇转动，因此它属于分度凸轮间歇运动机构. 平行分度凸轮机构是一种具有多个从动滚子共轭的机构[4]，较常见的是两片式结构，可见至少两个平面凸轮与多个滚子才能组合构成平行分度凸轮机构. 平行分度凸轮机构相较于其他间歇运动机构，结构更为复杂，动态性能与降噪性能更佳. 目前平行分度凸轮机构的结构类型大致可以分为外接式、内接式和直动式三大类. 传动机构中的凸轮以角速度ω进行转动，通过轮廓从而使得分度盘进行有规律的间歇分度运动. 平行分度凸轮机构的动力性能与凸轮轮廓曲线紧密相关，对此了解凸轮廓形是非常必要的.

1.2 平行分度凸轮机构理论凸轮廓线

每个凸轮会推动相应的滚子围绕分度盘中心运转，也就是说，每个滚子的廓线都体现在凸轮廓形上. 换言之，凸轮完整的轮廓曲线实际上是由多个凸轮廓线相交组合而成的[5]. 因此，完整的凸轮轮廓曲线需对每个滚子对应的凸轮廓线进行拼接. 图1为平行分度凸轮机构的轮廓曲线形成示意图，利用相对运动法可对凸轮廓形进行研究.

图1中Ro为凸轮基圆半径，计算式为

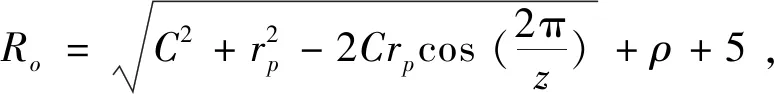
其中ρ是滚子半径.

对于No.1滚子来说，其接触的理论凸轮廓线K1可通过建立图2所示的坐标系的方式实现. 具体的计算表达式如下[6]：

xt1=rpsin (θ+φ-φ10-λ1)-Csin (θ-

φ10-λ1)

(1)

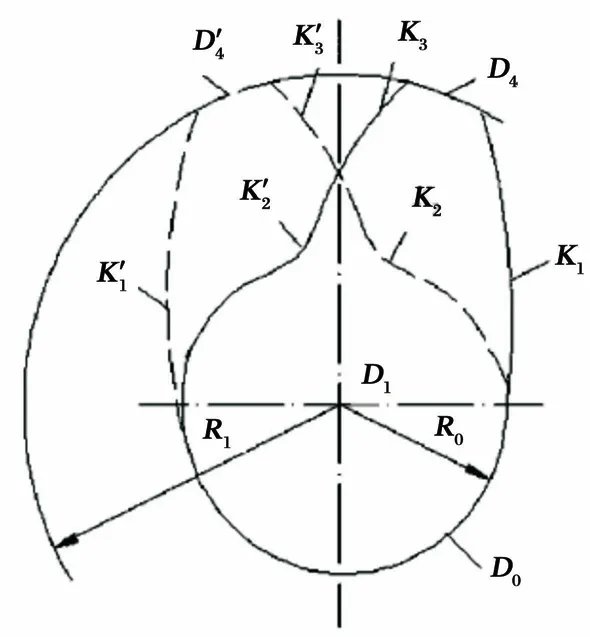
图1 凸轮轮廓曲线形成简图

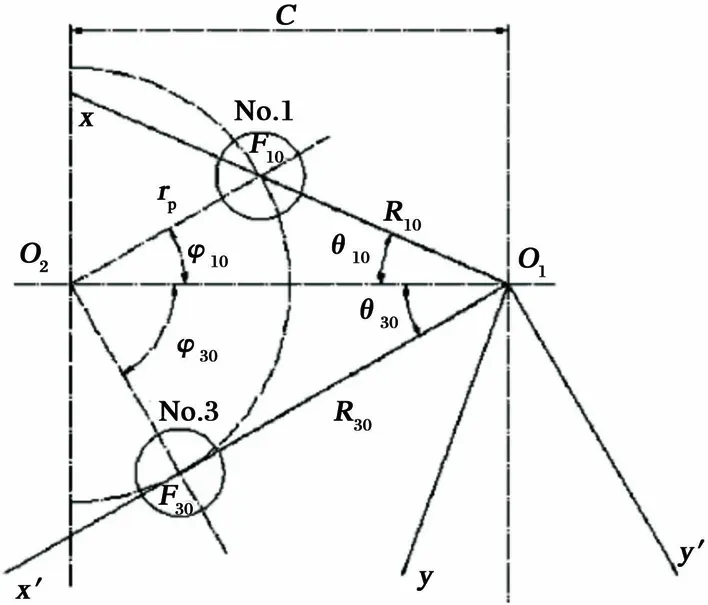
图2 滚子No.1与No.3间理论凸轮廓线标系建立

yt1=-rpcos (θ+φ-φ10-λ1)+Ccos (θ-

φ10-λ1)

(2)

其中，rp表示的是分度盘节圆半径；C代表分度盘中心点与凸轮中心点之间的距离；θ为凸轮的角位移；φ与φ10分别代表的是分度盘的基准初始位置角与角位移；λ1则是计算时所用到的辅助角，可根据式(3)计算获得.

(3)

图3是No.1滚子的轮廓曲线坐标建立图. 从

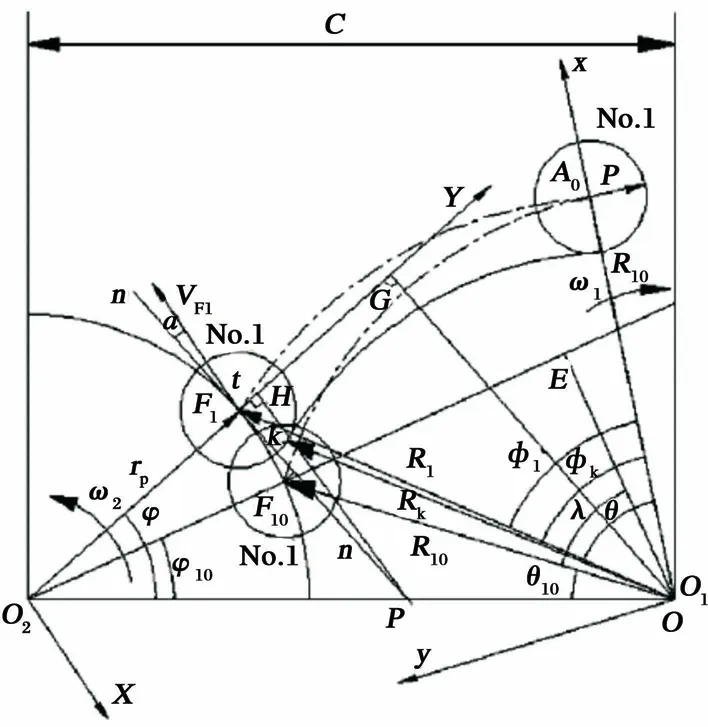
图3 No.1滚子的轮廓曲线坐标建立

x't=rpsin (θ+φ-φ30-λ3)-Csin (θ-φ30-λ3)

(4)

y't=-rpcos (θ+φ-φ30-λ3)+Ccos (θ-

φ30-λ3)

(5)

xt3=x'tcos (θ10-θ30)-y'tsin (θ10-θ30)

(6)

yt3=x'tsin (θ10-θ30)+y'tcos (θ10-θ30)

(7)

式(4)与式(5)中的λ3是计算辅助角，可依据式(8)计算获得.

(8)

图2是滚子No.1与No.3间理论凸轮廓线标系. 由图2可知，θ10表示No.1滚子在初始φ10位置处时F10O1和中心距线段O1O2之间的夹角，θ30表示No.3滚子在初始φ30位置处时F30O1和中心距线段O1O2间的夹角.

1.3 平行分度凸轮机构工作凸轮廓线

滚子No.1、滚子No.3所接触的实际工作凸轮廓线的运算公式如式(9)至(14)所示：

xk1=xt1-ρcos (θ+φ-φ10-λ1+α)

(9)

yk1=yt1-ρsin (θ+φ-φ10-λ1+α)

(10)

x'k=x't-ρcos (θ+φ-φ30-λ3+α)

(11)

y'k=y't-ρsin (θ+φ-φ30-λ3+α)

(12)

xk3=x'kcos (θ10-θ30)-y'ksin (θ10-θ30)

(13)

yk3=x'ksin (θ10-θ30)+y'kcos (θ10-θ30)(14)

其中，α是压力角，求取公式为

(15)

其中ω1、ω2分别为凸轮角速度、分度盘分度期的角速度.

2 平行分度凸轮传动机构CAD/CAM系统设计

2.1 总体设计

本次CAD/CAM系统设计采用C++语言开发，根据应用需求设计凸轮运动机构. 本次系统总体设计的内容共包括以下4个方面：一是可选择凸轮机构从动件运动规律； 二是凸轮参数设计以及确定参数的合理性； 三是可对凸轮轮廓与压力角等进行设计并进行运动仿真； 四是数控加工文件与轮廓仿真等数据输出.

2.2 界面设计与实现

结合上述总体设计需求以及平行分度凸轮传动机构的运动特点，此次CAD/CAM系统设计共分为运动循环设计、凸轮参数设计与凸轮运动仿真等模块.

2.2.1 运动循环设计

平行分度凸轮的从动盘机构不同于普通的凸轮，其运动具有周期性，共分为转动期与休止期. 因此，反映到凸轮运动规律上也同样是具有周期性的，并且速度、方向不会改变，位移曲线应该在0至1的范围内单调递增[8]. 对此采用C++语言进行设计，设计效果如图4所示，该设计模块共包含了40余种常见运动规律，可通过对运动规律的各段进行等分数据点数量设定来提高计算精度. 图4中设置动程角，多项式的运动曲线，所显示的运动循环效果图如图5所示.

图4 凸轮运动循环设计模块界面

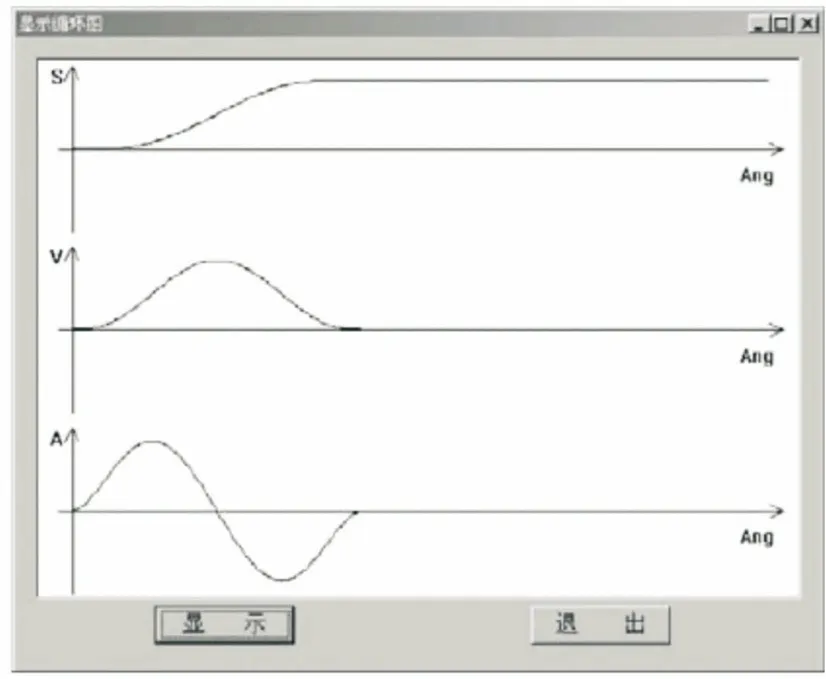
图5 运动循环效果图

2.2.2 凸轮参数设计

对于平行分度凸轮机构设计而言，参数确定是重要的设计环节. 凸轮的参数将直接影响凸轮的动力性能，因此，在凸轮机构设计中非常注重对凸轮的头数、中心距、节圆半径、滚子半径、分度盘以及分度盘转角的参数化处理. 凸轮参数设计界面如图6所示. 在此模块中，可对凸轮的几项重要参数进行设置，并且可在右边对设计的平行分度凸轮进行二维预览. 但是凸轮参数设计并非随意为之，而是需要通过压力角等判断条件来优化参数，从而来确保凸轮轮廓曲线的合理性.

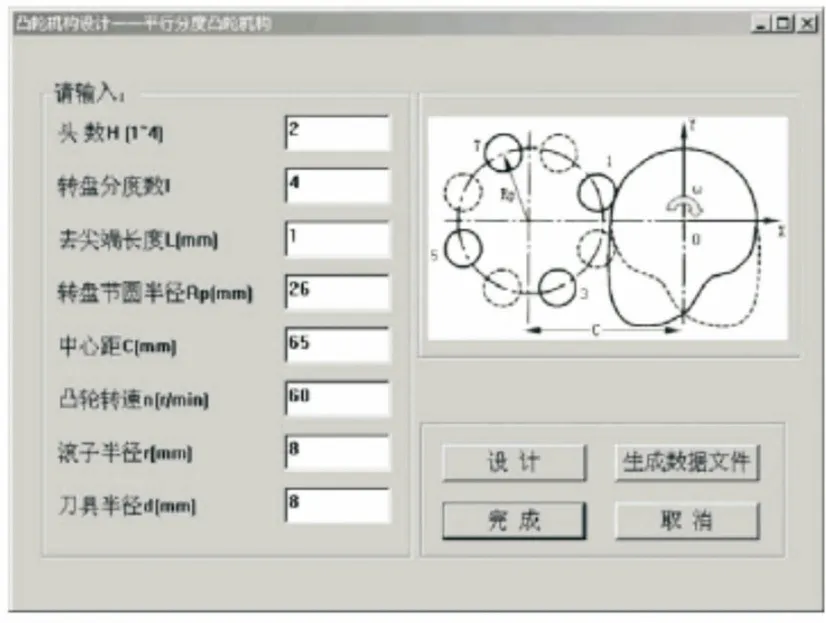
图6 凸轮机构参数设计界面

2.2.3 NC代码生成

平行分度凸轮机构的凸轮廓线是由多段曲线构成的. 在计算滚子No.1、滚子No.3的凸轮廓线后，其中向径较短的为分度期的廓线，其余的则为停歇期的廓线，然后用相切的圆弧封闭即可得到完整的凸轮轮廓曲线数据. 随后就可在UG环境下生成凸轮轮廓模型图，然后就可进行加工仿真，并自动生成NC代码. 该模块的部分源代码如下所示. 通过该模块的仿真结果来校核设计的平行分度凸轮机构的啮合情况.

viod ClnputDlg: :intersection ( )

{int u=0, v=0, j; double min, t;

min=( Xc [0] -Xcl [0]* (Xc [0]-

Xcl [0]) + (Yc [0] - Ycl [0]) * ( Yc [0] - Ycl [0]);

for (int i=0; i < num; i + +)

{for (j=0; j < num; j + +)

{t =(Xc [i]- Xcl [j]) * (Xc [i]-

Xcl [j]) + Yc [i]- Ycl [j]) * Yc [i]-

Ycl [j])

if (min >t)

{min=t; u=I; v=j;}

}

}

… …

}

3 平行分度凸轮传动机构运动仿真

为设计动力性能更好的平行分度凸轮传动机构，对其进行动力仿真是必不可少的，这能有效地对设计的凸轮机构进行修正. 对此，在Pro/E的应用环境中，利用Mechanism/Pro接口来实现与Adams系统仿真功能的无缝对接. 根据前面设置的参数与运动规律，获得的平行分度凸轮机构运动仿真如图7所示. 利用仿真系统对No.1滚子的角速度与角位移数据进行测试，测试结果见图8. 从图8中不难看出，本次设计的平行分度凸轮传动机构结构是合理的，动力性能满足要求.

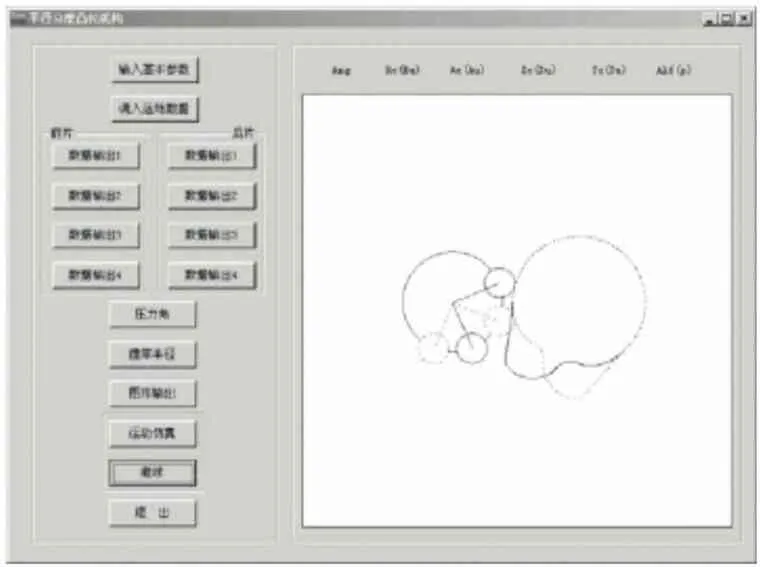
图7 设计平行分度凸轮机构运动仿真图

图8 No.1滚子角速度与角位移曲线

4 结论

在基于凸轮机构传动原理的基础上，利用Pro/E软件实现了平行分度凸轮机构CAD/CAM设计系统的开发，在系统中实现凸轮工作轮廓曲线的计算，并进行了运动仿真，来进一步校验设计的凸轮机构的合理性，从而修正设计参数. 该系统极大地提高了设计效率，通过仿真校验等多种手段确保了平行分度凸轮机构的质量.