基于R 语言的ARIMA 乘积季节模型对重庆某儿童医院门诊量的预测分析

唐 路，宋 萍，谢冰珏，佘 颖

（重庆医科大学附属儿童医院病案统计科，重庆 400014）

门诊医疗服务工作通常具有点多、线长、面广的特点，是医疗活动的首要环节，关系到医院的整体形象[1]。门诊量在很大程度上直接反映出医院规模、医疗技术水平、管理水平及患者对医院的信任度[2]。我院是集医教研为一体的国家三级甲等综合性儿童医院，在全国最佳医院排行榜中连续多年位居全国儿童医院第三位。2019 年医院日均门诊量0.92 万人次，门诊外埠患者比例近20%，加上儿童就诊特殊性，极易形成短时间内人流量高峰，增加排队时间，从而引发医患矛盾。求和自回归移动平均（auto regressive integrated moving average model，ARIMA）在门诊量预测中已得到了广泛应用，且预测效果较好[2-4]。本文通过对我院月门诊量时间序列数据进行预测分析，了解其变化特点及规律，以期为医院合理配置人力资源及医疗物资提供有力支撑，增强现代医院的门诊综合服务能力及效率。

1 资料与方法

1.1 资料来源 数据来源于重庆医科大学附属儿童医院病案统计科2009 年～2019 年医院业务量月报表，其中2009 年～2018 年逐月数据用于建立时间序列预测模型，2019 年逐月数据用于模型效果检验及预测评价，数据真实可靠。

1.2 方法 ARIMA 模型全称为求和自回归移动平均模型，该模型是由1970 年美国统计学家G.E.P.Box和英国统计学家G.M.Jenkins 提出的一种经典时间序列预测模型[5，6]。ARIMA 模型可对具有季节效应的时间序列进行建模，根据季节效应的提取难易程度分为简单季节模型ARIMA（P，D，Q）S 和乘积季节模型ARIMA（p，d，q）×（P，D，Q）S。因门诊量时间序列既有季节效应又有长期趋势效应且和随机波动之间存在比较复杂的交互影响，所以本文采用混合效应的乘积季节模型ARIMA（p，d，q）×（P，D，Q）S，其中p、d 和q 分别表示非季节自回归阶数、差分阶数和移动平均阶数；P、D 和Q 分别表示季节自回归阶数、季节差分阶数和季节移动平均阶数，S 为季节差分周期[6-8]。

乘积季节模型建模步骤[9-10]：①时间序列平稳化：ARIMA 模型的使用前提条件是数据必须是平稳的时间序列数据。应用时序图、自相关函数图初步识别序列趋势性、季节性等特征，采用单位根检验判断序列的平稳性。对于非平稳时间序列则需进行自然对数转换、非季节差分、季节差分等预处理，直到序列平稳为止。②模型参数定阶：根据差分次数确定d、D 阶数，p、q 和P、Q 阶数依据平稳序列的自相关函数图及偏相关函数图拖尾、截尾特征来确定。R软件中的auto.arima 函数可以进行最优模型自动筛选[11，12]。筛选依据：赤池信息准则（AIC）或贝叶斯信息准则（BIC）最小，对数似然函数值（Log likelihood）最大的模型为最优模型。③模型的检验：采用Ljung-Box test 判断模型的适合性，若残差满足白噪声，该统计量应没有显著性，否则模型需要进行改进。④模型预测：以2009 年～2018 年逐月门诊量数据进行模型拟合，筛选出最优乘积季节模型。再用2019 年逐月门诊量数据检验模型预测效果，根据预测值与实际值的平均绝对百分比误差（MAPE）评价预测效果。，其中Xi为原始数据，为预测值，N 为数据个数。

1.3 统计学分析 采用Microsoft Excel 2016 建立数据库，应用R-3.6.3 软件中的tseries 程序包和forecast 程序包进行数据处理和统计建模，以P＜0.05 表示差异有统计学意义。

2 结果

2.1 2009 年～2018 年门诊量时序图 依据我院2009年～2018 年门诊量数据绘制原始序列时序图，见图1。2009 年～2018 年我院门诊量总体呈现上升趋势，且有明显的季节波动特征，每年的5～7 月份出现第一个高峰期，之后有所回落，在11～12 月份再次出现高峰。

图1 原始序列时序图

2.2 时间序列平稳化 由于原始序列时序图存在上升和季节波动趋势，且经单位根检验差异无统计学意义（Dickey-Fuller=-2.9882，P=0.1656），因此判断原始序列不满足ARIMA 模型建模要求。为了消除原始序列的时间趋势，对其进行一阶非季节差分和一阶季节差分处理，处理后经单位根检验差异有统计学意义（Dickey-Fuller=-12.3890，P=0.01），时间序列数据已平稳，满足建模前提。

2.3 模型参数定阶 绘制平稳时间序列的时序图、自相关图（ACF 图）和偏自相关图（PACF 图），见图2。可以看出，平稳序列的ACF 和PACF 均拖尾，由此可以判断模型适用于ARIMA（p，d，q）×（P，D，Q）S。因对原始序列进行了一阶非季节差分和周期为12个月的一阶季节差分，所以d=1，D=1，S=12，初步确定模型为ARIMA（p，1，q）×（P，1，Q）12。对于p、q 和P、Q 阶数的判断可以从平稳序列的自相关函数图及偏相关函数图拖尾、截尾的特征得到启示，且根据历史文献参考超过两阶的情况较少[13，14]。本文利用R软件中的auto.arima 函数自动筛选最优模型，得出参数分别为：p=1、q=2，P=2、Q=0，因此经筛选得出最优模型为ARIMA（1，1，2）×（2，1，0）12。

图2 平稳序列相关图

2.4 模型检验 最优模型ARIMA（1，1，2）×（2，1，0）12 的赤池信息准则AIC=2315.69，贝叶斯信息准则BIC=2334.46，模型中各参数检验均有统计学意义（P＜0.05），见表1。采用Ljung-Box 方法对模型残差进行检验，检验统计量Q=6.3022，P=0.3902，模型残差为白噪声序列。同时对残差序列做自相关图（图3）和偏相关图（图4）。此模型残差大部分都落入95%可信区间内，序列信息已经被充分提取，得到的模型是适合的拟合模型。

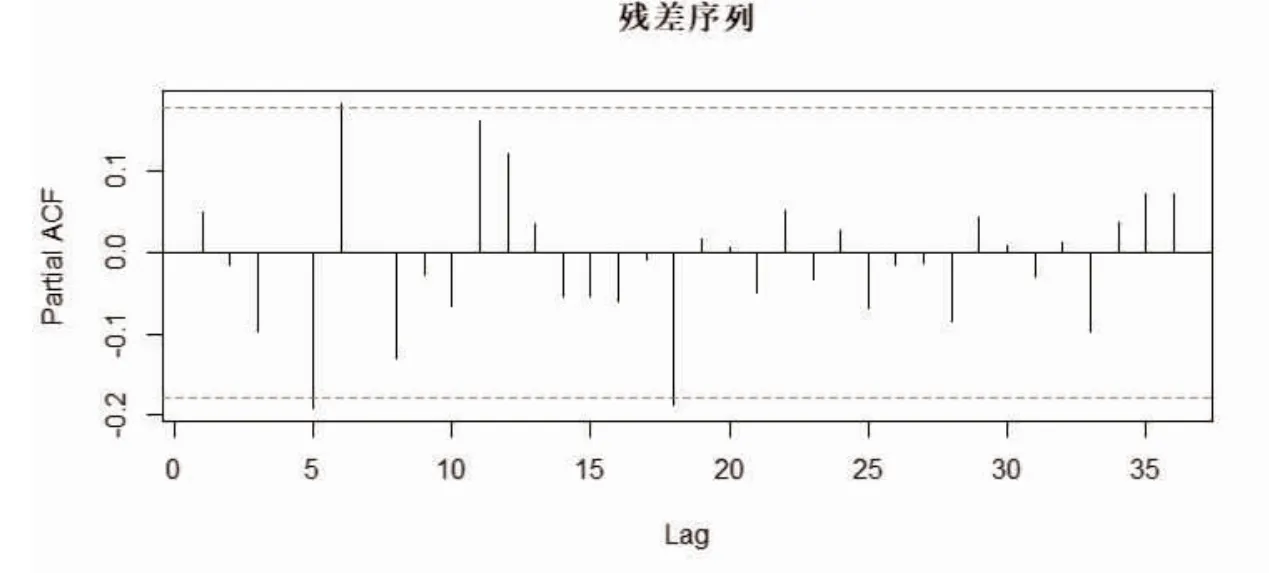
图4 模型残差偏相关图

图3 模型残差自相关图

表1 ARIMA（1，1，2）×（2，1，0）12 预测模型参数检验

2.5 模型预测 运用ARIMA（1，1，2）×（2，1，0）12 模型预测2019 年1 月～12 月门诊量，预测值与实际值对比情况见表2，实际值均在月门诊量预测值的95%可信区间以内，平均绝对百分误差6.56%＜10%，预测模型精确度较高。

表2 某儿童医院2019 年1 月～12 月门诊量预测值与实际值比较

表2（续）

3 讨论

随着社会经济发展，人们就医意识不断增强，及时就诊成为人们的迫切需求[15]。儿童作为一个特殊群体，面对二孩政策放开，公立医院应及时整合医疗资源来优化儿童门诊，以便满足日益增长的儿童卫生服务需求，提高儿童卫生服务效率，保证儿童健康水平。因此，科学准确的短期门诊量预测在医院日常管理和经营决策中具有重要意义，是现代医院管理的重要内容。及时掌握门诊量的变化趋势可以为医院合理开设门诊科室、配置医护人员等资源配置提供基础数据，同时节约医疗业务成本，提高医院的经济效益，有利于公立医院社会效益的实现[16]。

越来越多的预测模型在门诊量短期预测中得到广泛应用，如线性回归预测、灰色GM（1，1）预测、指数平滑模型预测、ARIMA 模型预测等[17]。不同的模型各有其优缺点及适用范围，其中，ARIMA 模型在医学领域的应用较为广泛，主要适用于有季节变动的数据，在短期预测上精确度较高。R 软件作为一款开源软件，在处理时间序列数据时具有强大的统计运算及绘图功能，本研究利用R 语言，通过时间序列数据预处理、模型参数定阶、模型检验等步骤，最终拟合得到门诊量ARIMA（1，1，2）×（2，1，0）12 模型，进一步对该模型残差分析发现，该模型较好地模拟了我院月门诊量时间序列变化趋势。利用该模型预测2019 年逐月门诊量，预测值与实际值的平均绝对百分比误差为6.56%，实际值均在预测值95%可信区间内，提示模型预测精准度较高。

综上所述，本研究建立的ARIMA 乘积季节模型为相对最优模型，且适合门诊量的短期预测，预测结果对医院合理配置人力资源具有实际应用价值，医院可以根据预测结果采取如下措施：①提前在门诊高峰时间、季节尽可能多增加知名专家门诊的坐诊人数，周末适当增加专家或专科号，增强门诊医疗技术力量。②实施弹性排班、分时段预约等措施，合理配置门诊医疗资源，发挥人、财、物资源的最大效益。③对于慢性患者，健康宣教时尽量提醒他们在门诊低峰时就诊，既可缓解门诊高峰时的就诊压力，也可节约患者的等待时间，从而缓解医患矛盾。但门诊量的变化是由多因素联合作用引起的，某些因素的改变可能会使得拟合模型不适用，如政策因素、传染病疫情流行与暴发。同时，ARIMA 模型由于其模拟的原理，对数据要求不高，只适合短期预测，因此下一步可以考虑通过组合模型进行预测，不断提高模型预测精确度。