遗传编程在医院日门诊量预测中的应用

大连理工大学经济管理学院(116023)

刘晓冰 顾福来△

【提 要】 目的 医院门诊量预测对于提高医院的工作效率具有重要意义。方法 针对日门诊量预测问题，提出一种基于遗传编程的日门诊量预测方法，该方法首先采用基于距离的离群点挖掘算法识别节日效应的有效时间范围。同时，用节气作为表示气候变化的最小时间单位，以及其他若干属性来描述日门诊量历史数据。最后，以遗传编程为框架，提出了日门诊量预测函数的分段学习策略。结果 算法对日门诊量的预测结果的决定系数均在0.9以上。结论 遗传编程方法具有较强的日门诊量预测能力。

门诊作为医院医疗服务的第一道窗口，为居民提供早期诊断，开展及时治疗，具有服务面广、随意性大和可控性小等特点。门诊服务水平直接影响患者的就医体验和医院的工作效率[1]。门诊量预测是根据门诊量的发展变化规律，预计和判断其未来发展趋势和状况的活动。准确的门诊量预测对提高医疗资源的利用效率具有重要意义，可以根据门诊量预测的结果动态安排出诊医师及导医、收费及药房等窗口服务人员，合理调配诊室数，从而缩短患者就医时间，维持良好的门诊秩序。

门诊量预测的研究可分为以下三种方法：(1)统计预测方法，即采用数理统计方法研究门诊量的变化规律。(2)人工智能方法，即采用人工智能算法(如神经网络，遗传算法)学习门诊量数据的规律，(3)混合方法，即将统计预测和人工智能方法相结合。上述预测方法在门诊量的预测上取得了一定的成果，但目前的研究还存在如下问题：(1)预测时间粒度较粗：目前研究主要以季度或月份为单位进行预测，鲜有日门诊量的预测研究。事实上，日门诊量对医院每天的工作安排更有指导意义，相反，以季度或月份为单位的门诊量预测缺乏实际的工作指导意义；(2)鲜有节假日的门诊量预测：准确预测节假日门诊量对合理安排医护人员的休假有重要指导作用，可缓解“医护人员过劳”的普遍状态；(3)缺乏门诊量的节日效应研究，所谓的节日效应是指门诊量在某节假日的前或后的一段时间内，日门诊量数据发生异常变化。

本文提出了一种日门诊量预测方法，首先采用“节气”等数据特征来描述日门诊量历史数据，相比于季节和月份，节气更准确地反应了气候变化的规律和对疾病的影响；然后，采用基于距离的离群点挖掘算法识别节假日门诊量的节日效应的时间范围，为节假日的门诊量预测奠定数据基础；最后，基于遗传编程(genetic programming，GP)，设计了日门诊量的预测学习算法。

数据预处理和节日效应识别

1.数据描述

本文所使用的数据为大连市某三甲医院2015年1月1日至2017年12月31日期间共计1096条日门诊量的历史数据，如图1所示。由图1观察可知：日门诊量数据呈逐年上涨趋势，且具有季节性波动特征。全部数据的部分统计特征如下：均值为5500，方差为4653076，最大值为9639，最小值为619。

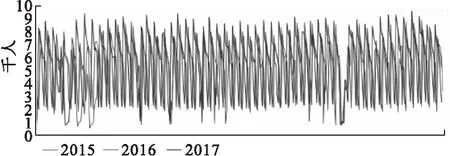
图1 2015年1月1日至2017年12月31日的日门诊量

2.数据准备

参考相关文献[2-3]，本文将描述日门诊量数据的特征或属性集合定义为:

{year，season，month，day，weekday，festival，festIndex，outpaNo}

其中，year={2015，2016，2017}表示年份；season={1，2，3，4}表示季度，1为第一季度，其他依次类推；month={1，2，…，12}表示月份，1为一月，其他依次类推；day={2015/01/01，…，2017/12/31}表示具体的日期；weekday={1，2，…，7}表示该天是星期几，1为星期一，其他依次类推；festival={0，1，2，3，4，5，6，7}表示节假日类型，0表示非节日，1为元旦，2为春节，3为清明节，4为五一劳动节，5为端午节，6为中秋节，7为国庆节；festIndex={1，2，…，n}表示某节假日内的第几天，1为该节假日内的第一天，其他依次类推；outpaNo表示该天的门诊量。

表1展示了2016年春节前后一段时间的日门诊量，数据显示春节期间的日门诊量急剧下降。

表1 2016年春节前后一段时间范围内的日门诊量

3.预测评价指标

使用均方根误差(root mean square error，RMSE)和决定系数(coefficient of determination，R2)作为预测结果的评价指标，定义如下：

4.特征集调整

ARIMA模型和SARIMA模型是当前常用的预测门诊量的时间序列预测模型[4-6]，二者区别在于SARIMA更适用于具有季节性波动的时间序列预测。图1可知日门诊量具有显著的季节性波动特性，因此本文采用SARIMA模型进行初步预测，预测结果为：R2=0.773，RMSE=1029.418。图2显示了全部三年的日门诊量预测结果，图3详细地显示了2016年2月的预测结果，其中，2016年2月7日为春节，该天的日门诊量为747，SARIMA预测结果为4532。

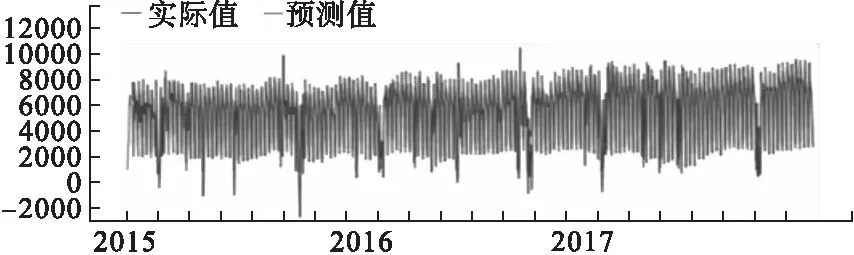
图2 2015年1月1日至2017年12月31日的预测结果

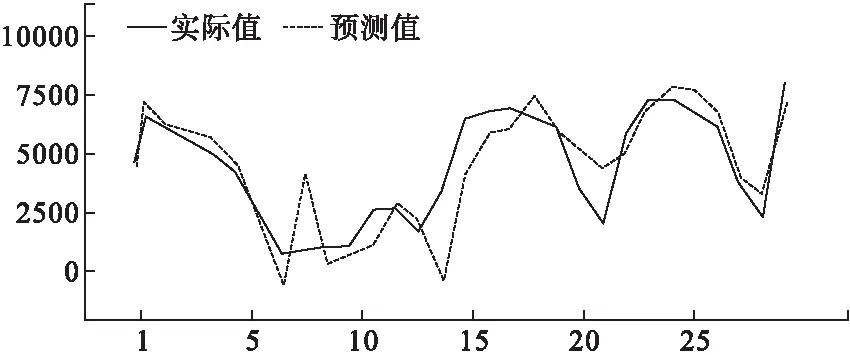
图3 2016年2月的预测结果

SARIMA模型预测结果显示：日门诊量的预测值与实际值的误差较大，特别是节假日以及节假日前后一段时间范围内的日门诊量的预测值很大程度偏离实际值。经过分析，造成预测误差较大的可能原因如下：

(1)节假日的日门诊量较非节假日的日门诊量有显著下降，特别是重要节日，如春节，国庆等节；

(2)日门诊量存在节日效应，所谓的节日效应是指在节假日的前后一定时间内，日门诊量数据异常变化；

(3)日门诊量与医院所在地的气候条件存在较密切的关系[7]，而季度和月份两个时间特征反应气候变化的粒度较为粗糙，同一个季度和月份的在不同的年份的同一天，可能在气候上存在显著差异；

(4)ARIMA和SARIMA模型在日门诊量的预测上能力不足，目前，这类模型主要用于月度和季度的门诊量预测，如文献[4]和[5]，鲜有日门诊量预测的案例。

此外，自然界现象周期性、节律性变化，直接或间接地影响着人体，而节气的划分充分考虑了季节、气候、温度、湿度等自然现象的变化以及变化的滞后效应。因此很多医学研究表明，人体疾病的发生发展与“二十四节气”有密切关系[8-9]。为此，本文根据SARIMA模型的分析结果以及节气对疾病的影响的事实，将描述日门诊量数据的特征集合调整为：

{year，month，solarTerm，weekIndex，weekday，festival，festIndex，festEffitive，outpaNo}

其中，新的特征定义如下：solarTerm={1，2，…，24}表示24节气，1为小寒，其他按照“二十四节气”的顺序依次类推；weekIndex={1，2，3}表示在当前节气内的第几周，1表示当前节气内的第一周，其他依次类推，由于每个节气最多16天，weekIndex的最大取值为3；festEffitive={-nb，…，-1，1，…，na}表示节日效应的时间范围，-1表示某节假日有节日效应的节前第一天，1表示某节假日有节日效应的节后第一天，其余依次类推，需要说明的是：节日效应变量nb和na具有如下特征：(1)该节假日的节前的第nb天和该节假日节后的第na天一定有节日效应；(2)该节假日的节前的第nb+1天和节后的第na+1天一定没有节日效应；(3)对于同一节假日，nb和na可能不相等。

根据调整后的特征集合，表2重新给出了表1中的数据(2016年春节的nb=2，na=4，后文给出计算方法)。需要说明的是，每年的任意一天可由属性year，solarTerm，weekIndex和weekday上的取值唯一确定。

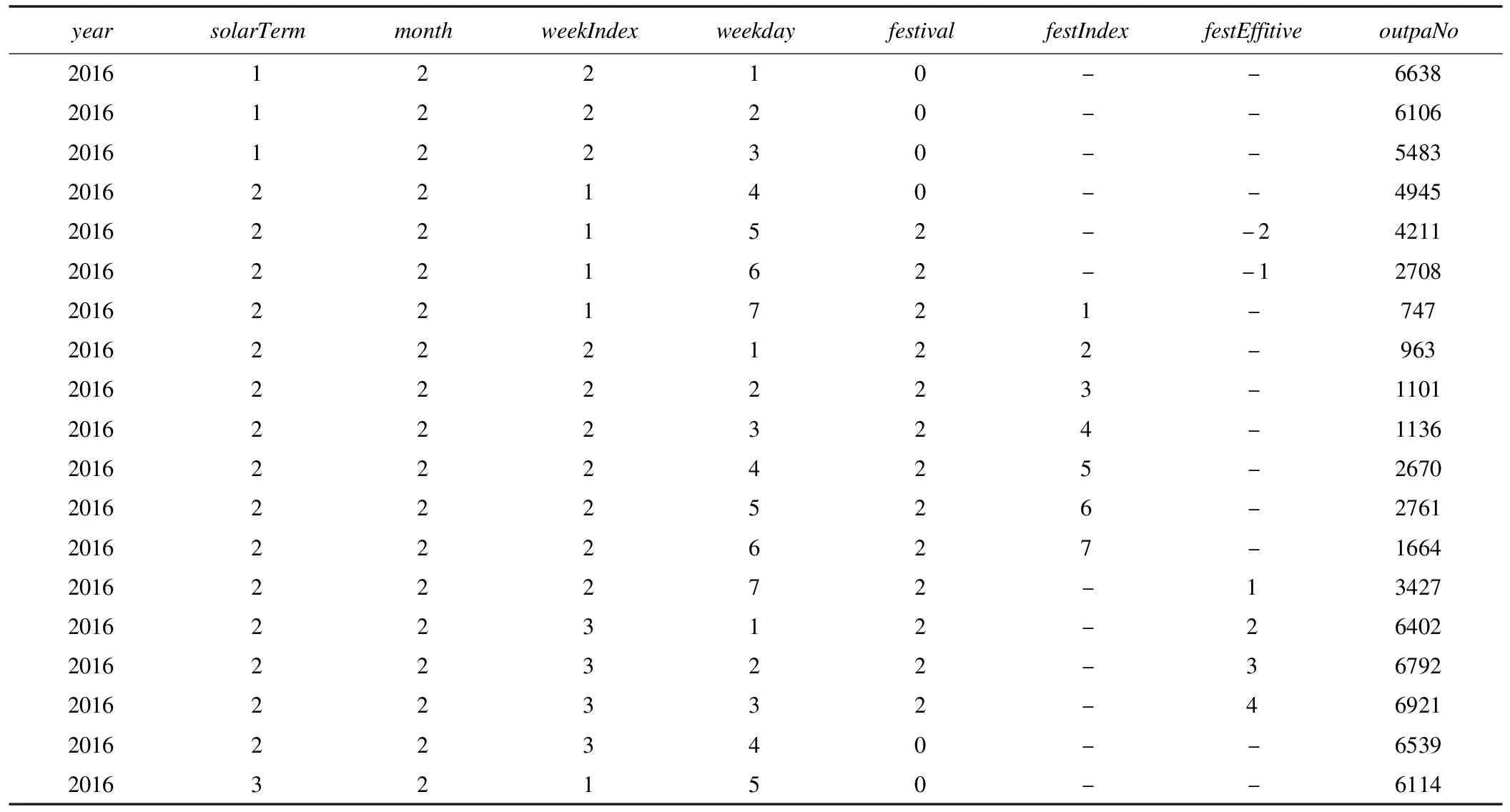
表2 2016年春节前后一段时间范围内的日门诊量(新)

5.门诊量的节日效应识别

节日效应广泛存在于股市、期货、旅游等领域。显然，日门诊量存在明显的节日效应，它是指节假日对日门诊量的波动产生的影响(不包括节假日本身)，且可能同时存在节前效应和节后效应，即节假日前后一定时间的日门诊量发生异常变化，或显著增加，或显著减少。

为了识别门诊量的节日效应，首先需要确定节日效应的时间范围，即nb和na。本文将采用识别离群点的方法确定节日效应的时间范围，即：若某节假日的节前或节后的某天的日门诊量发生异常变化，则该天的日门诊量是相对于该天一定时间范围内的日门诊量数据集的离群点(outlier)。离群点挖掘算法通常有基于统计、基于距离、基于深度、基于密度和基于聚类等方法[10]。由于门诊量的节日效应仅由节假日造成，因此，日门诊量的节日效应属于低维度离群点挖掘，本文选用基于距离的离群点挖掘算法来识别节日效应的时间范围。需要说明的是基于距离的离群点挖掘算法对于低维度数据特别有效[9]。

确定节日效应的时间范围，首先需要确定节假日前或后的某天的日门诊量是否为离群点，为此，本文设计了如下的离群点识别算法(lth_Day_Check)：

(1)

(2)

(3)

以2016年春节为例(数据见表2)，针对春节后第一天(即2016年2月14日)，确定该天是否有节日效应，该天为星期日，假设k=8，λ=0.6，数据集db(7，1，9)的实际取值为{3427，2158，1725，1687，2053，2074，2250，2469，2277}，其中，第一个数据(3427)为春节后第一天的日门诊量，其他8个数据为该天前后4个同为星期日的正常日期的日门诊量。计算可知：Mean_outpaNo=2236.56，maxdb(7，1，9)=3427，mindb(7，1，9)=1687。式(1)计算结果为vu=3280.56，小于3427，因此该天疑似有节日效应。由式(2)、式(3)可得：P=0.89，r=98.56。通过计算可知该天的日门诊量与数据集中db(7，1，9)中除自身之外其他天的日门诊量的距离均大于r，故该天的日门诊量为数据集db(7，1，9)的离群点，即：2016年春节后的第一天存在节日效应。

在算法lth_Day_Check的基础上，确定某个节假日x的节日效应的时间范围的完整算法如下：

Step1:sum_nb=sum_na=0

Step2:foreachy∈year

Step2.1:采用lth_Day_Check算法，确定该节假日在本年度的假日效应参数nb，y和na，y

Step2.2:sum_nb+=nb，y，sum_na+=na，y

Step3:end for

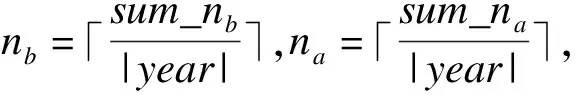
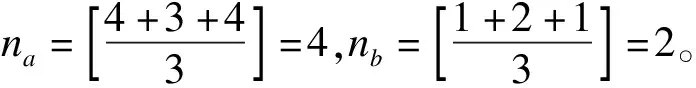
基于遗传编程的日门诊量预测算法

1.基于遗传编程日门诊量预测算法概述

遗传编程(GP)是由Koza教授提出的一种人工智能算法[11]，它采用分层结构表示解空间，且结构大小可变。遗传编程广泛应用于预测、符号回归等领域。本文基于遗传编程，结合函数符号集与终端符号集，随机产生日门诊量的预测表达式(即初始群体)，通过选择，交叉和变异等操作进行日门诊量预测表达式的学习。下面将从编码、选择和适应度评价、交叉、变异四个方面进行介绍。

(1)编码

个体编码的基因值来源于函数符号集与终端符号集，其中，函数符号集由数学运算符号构成，终端符号集由问题的输入变量和常数构成。本文中，个体编码为树状结构组织，并采用“生长法”产生初始群体，其步骤如下：预先给定一个树的最大深度(即节点层数)，之后随机从函数符号集中选择一个元素作为根节点，然后随机产生与该元素所对应的函数的操作数数目相同的子树，如果某个节点的深度小于给定的最大深度，则随机从函数符号集或终端符号集中选择一个元素填充该节点，若深度等于最大深度，则从终端符号集中选择一个元素填充该节点。

(2)选择和适应度评价

在适应度评价结束后，采用锦标赛算子选择个体参与交叉和变异。锦标赛算子基本操作如下：假设锦标赛规模为m，随机从父代种群中选择m个个体，m个个体中适应度最好的个体被选中。此外，本文还使用了精英保留策略，即保存每代适应度最好的个体。

(3)交叉

交叉是产生新个体的主要操作，新个体继承父代基因并产生新基因。本文采用的交叉操作如下：随机从种群中选择两个个体(P1，P2)作为父代，然后从每个父代中随机选择一个点作为交叉点，两个父代交换以交叉点为根节点的子树，得到新个体(O1，O2)。图4给出了一个交叉的例子。

图4 交叉

(4)变异

变异可以增加种群多样性，有利于算法跳出局部最优。本文的变异操作具体如下：随机从种群中选择一个个体作为父代，然后随机选择父代一个节点作为变异点，删除以该变异点为根节点的子树，最后随机生成一个新的子树插到该变异点。图5给出了一个变异例子。

图5 变异

2.分段学习

观察图1可发现，在不同的时间区间，门诊量的曲线形状有所不同，部分区间差异非常大。存在日门诊量预测函数的分段现象，即：不同区间的日门诊量预测表达式有所不同，不能采用一个统一的预测表达式来预测全部的日门诊量。本文采用分段学习策略来实现日门诊量预测函数的分段学习，其基本思想为：预先设定一个适应度阈值，采用GP算法进行预测表达式的学习。若所得预测表达式的适应度低于阈值，则任选一个特征进行分段并确定其分段边界，再根据分段情况分别生成预测表达式并进行预测学习，直到适应度达到阈值为止。

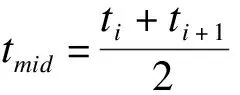
由于日门诊量数据的异常变化主要由节假日导致，因此，优先选择festival特征采用二分法进行分段学习。

实验结果

使用某三甲医院的1096条日门诊量历史数据作为实验样本，首先采用前面提出的特征定义和节日效应的时间范围确定算法进行数据预处理，之后采用遗传编程进行日门诊量的预测表达式的学习。GP的参数如下：种群规模为200，最大深度为10，交叉概率为0.8，变异概率为0.1，迭代次数500。函数符号集为{+，-，*，/，sin，cos，tan，log10，exp，ln，sqrt}，终端符号集为{X0，X1，X2，X3，X4，X5，X6，X7}∪{1，2，3，5，7，11，13，100}。各变量含义为：X0代表年份；X1代表月份；X2代表节气；X3代表节气的第几周；X4代表星期几；X5代表节假日类型；X6代表某节假日内的第几天；X7代表节日效应的时间范围。{1，2，3，5，7，11，13，100}为常量集，常量集主要由1～13的素数构成，这样的常量集有助于预测表达式中常数项的挖掘[13]。

为了避免学习过程中的过拟合和欠拟合等问题，采用如下方式进行实验：若某一待学习区间的样本数量大于50，则将75%的数据作为学习集，25%数据作为测试集；否则，采用“留一法”，即：假设有k个样本，每次只留下一个样本做测试集，其他样本做学习集，共学习k次，选择适应度最高的预测表达式作为最终结果。

具体实验结果如表3所示，表中“函数分段条件”列中的所有节假日均表示某节假日以及该节假日的具有节日效应的区间。

表3 日门诊量预测的实验结果

由实验结果可知：R2均在0.9以上，表明日门诊量预测表达式能够解释门诊量预测中90%以上的因素，证明本文的日门诊量预测方法有很好的预测能力。其中，非节假日(即：X5=0且X7=0)的日门诊量预测表达式，在学习集上的预测精度为：R2=0.9381，RMSE=498.6147；在测试集的预测精度为：R2=0.98163，RMSE=463.0586。测试集的预测结果如图6所示。从图中可看出，非节假日的日门诊量预测值曲线和实际值曲线基本吻合。

图6 日门诊量预测值和实际值的对比

讨 论

由对比可知，本文所提出的算法的预测结果的R2均在0.9以上，相对于前述SARIMA模型的预测结果有显著提高，且克服了SARIMA模型在节假日及节日效应时间范围内预测精度较差的问题。此外，由实验结果可知，测试集的R2和RMSE均优于训练集，说明预测算法不存在过拟合的问题，且具有较强的泛化能力。

从实验可以看出，本文算法具有较好的日门诊量预测能力，其原因如下：(1)采用节气来标识气候条件的变化，细化了气候条件对日门诊量的影响；(2)基于距离的日门诊量节日效应离群点挖掘算法准确识别了节日效应的有效长度；(3)基于二分法的分段函数的分段策略，有助于日门诊量分段函数的挖掘。

结 论

针对医院门诊量分析与预测问题，首先根据日门诊量数据和SARIMA模型的预测结果不足进行分析，采用基于距离的日门诊量节日效应离群点挖掘算法进行节日效应的判别。为了更为准确判断气候变化对门诊量的影响，采用节气作为表示气候变化的最小单位。在此基础上，提出了分段学习策略，实现了基于遗传编程的日门诊量预测，取得了较好的预测效果。

在未来的研究中，可考虑在日门诊量预测时加入更多的特征，如空气质量、患者年龄、交通出行指数等因素对门诊量的影响等。也可在本文所提出的研究方法基础上，开展突发性公共卫生事件，如新冠肺炎等，对门诊量的影响研究。