5自由度角接触球轴承的静态特性分析

李震，关先磊，王青山，秦斌

（1.中南大学 高性能复杂制造国家重点实验室，长沙 410083；2.中南大学 交通运输工程学院 轨道交通安全教育重点实验室，长沙 410075）

随着旋转系统转速和精度的不断提高，轴承作为旋转系统的重要组成部件，对旋转系统中的转子起到重要支撑作用。轴承的种类繁多，且已经系列化和标准化。在众多轴承种类中，角接触球轴承能够同时承受径向力和轴向力，且具有较好的稳定性和良好的润滑特性，被广泛应用于机床主轴和电主轴等要求高转速、高精度和高稳定性的场合，其静态特性会影响旋转系统的工作性能。为了提高旋转系统的工作性能，有必要对角接触球轴承的静态特性开展研究。在此领域，国内外学者已经做了大量的研究工作，并取得了一系列成果。

师浩浩等[1]基于Hertz点接触理论建立了角接触球轴承的静态分析模型，并与传统简化算法对比，验证该模型的有效性和精确性。徐涛等[2]基于赫兹接触理论，采用有限元软件ANSYS建立角接触球轴承分析，研究其在外载荷作用下的静态接触特性。丁鸿昌等[3]在Jone-Harris刚度模型的基础上，建立一个基于沟道控制理论的5自由度角接触球轴承刚度模型，研究其静态刚度特性。Guo等[4]基于滚珠轴承动力学理论，提出四列角接触球轴承的静力学分析模型。Demul等[5]基于经典赫兹接触理论，提出一种新型的、通用的5自由度滚动轴承数值分析模型，可以实现滚动轴承静态特性的快速求解。同时指出，该模型所用到的理论也被称作“Demul理论”。任泓睿[6]采用Demul理论建立5自由度拟静力学分析模型，研究其静态接触特性。Liu等[7]提出了一种考虑轴向预加载和接触角的角接触球轴承内载荷分布和刚度的解析方法。研究了组合载荷对静态接触角、内载荷分布和轴向刚度的影响。Zhang等[8-9]基于琼斯模型建立角接触球轴承5自由度分析模型，研究其静态接触角和接触载荷的变化规律。Hong等[10]建立了角接触球轴承在不同预紧机构作用下的刚度比较模型，研究预紧力对轴承静态特性的影响。Wang等[11]采用无滚道控制理论建立角接触球模型，极大简化了模型的求解计算，并采用该模型研究轴承的静态特性。Bizarre等[12]建立了考虑非线性刚度和阻尼的5自由度角接触球轴承分析模型。

综上所述，现有角接触球轴承的静态分析方法基本上是基于琼斯和Jone-Harris模型展开的，但是计算量大，需要多次迭代求解，且求解精度较差。本文基于Demul理论和弹性赫兹接触理论，以角接触球轴承为研究对象，考虑轴承滚珠和滚道之间的弹性接触，从轴承内部几何关系入手，建立5自由度角接触球轴承的简化静态分析模型；然后将本文结果与文献结果进行对比，验证本文模型的准确性和有效性；最后利用该模型研究轴承外载荷对轴承静态参数的影响。本文模型考虑结构简单，具有较高的计算效率和精度，适用于复杂工况下角接触球轴承的静态特性求解，为确定最佳预紧载荷提供理论基础和技术指导。

1 理论推导

1.1 角接触球轴承的模型

如图1所示。考虑角接触球轴承5自由度的几何分析模型，在没有外载荷的条件下，角接触球轴承内外圈滚道的曲率中心与滚珠中心位于同一条直线上，即Oi,Oo,O3点共线，直线Oi,Oo与垂直于轴承内圈轴线方向所夹的角为αo。ri和ro分别表示内外圈滚道曲率半径；D表示滚珠直径。

Dm表示轴承节圆直径；Fx,Fy,Fz,Mx,My分别表示作用在轴承内圈上的外和外力矩，用F表示轴承内圈受到外力向量；Qr,Qz,M分别表示滚珠作用在轴承内圈上的力和力矩；rp和zp分别表示内圈滚道曲率中心的径向距离和轴向距离。

图1 轴承几何模型

如图2所示。描述了角接触球轴承在受力前后内外圈曲率中心以及滚珠中心位置的变化，Oi,Oo,O表示未受力的位置，Oʹi,Oo,Oʹ表示受力后的位置。从图中可以看到，外圈的曲率中心在受力前后没有发生改变，这是因为轴承在工作过程中，一般是内圈随转轴一起转动，外圈与轴承支座固定。A1j和A2j分别表示未受力前内外圈曲率中心的轴向距离和径向距离；和分别表示受力后内外圈曲率中心的轴向距离和径向距离；looj和loij分别表示轴承在受力前滚珠中心与内外圈中心之间的距离；loj和lij分别表示轴承在受力后滚珠中心与内外圈中心之间的距离；uz和ur分别轴承内圈在力作用下的轴向位移和径向位移；vz和vr分别滚珠在力作用下的轴向位移和径向位移。

图2 曲率中心的相对位置

根据图2所示的几何分析，可以得到受力后内外圈曲率中心的轴向距离和径向距离，进而可以得到内外圈曲率中心之间的距离。

受到外载荷后，轴承的接触角会发生改变，角接触球轴承在受力后的第j个滚珠与内圈的接触角用αj表示。

轴承的外圈固定在轴承支座上，当轴承受到外力时，轴承的内圈相对于外圈产生5个方向的位移。如图3所示。δx，δy，δz代表平动位移θx，θy代表转动位移,内圈相对于外圈的位移向量用δ表示。由上述分析可知单个滚珠也会对轴承产生作用力，作用在轴承内圈上的力向量用Qj表示，轴承内圈该力作用下产生的位移用ur，uz，θ表示，位移向量用uj。但是当轴承处于静态下，滚珠不会发生转动，即M=0，θ=0，故在图2中没有指出在滚珠作用下轴承内圈产生的转动位移。

图3 轴侧剖视图

将单个滚珠作用在轴承内圈所产生的位移ur，uz，θ视为轴承内圈在局部坐标系下的位移；将轴承内圈在外力作用下产生的位移δx，δy，δz，θx，θy视为轴承内圈在整体坐标系下的位移。为了建立5自由度的静态分析模型，需要建立ur，uz，θ和δx，δy，δz，θx，θy之间的关系。

为了建立上述变量之间的关系，需要进行从局部坐标系到整体坐标系的坐标变换，根据文献[5]，得到变换矩阵用Rj表示。

式（6）中的ψj表示滚珠方位角，可以参考图4所示的示意图，j表示第j个滚珠，与X轴相交的滚珠记为第1个滚珠，N表示滚珠的个数。

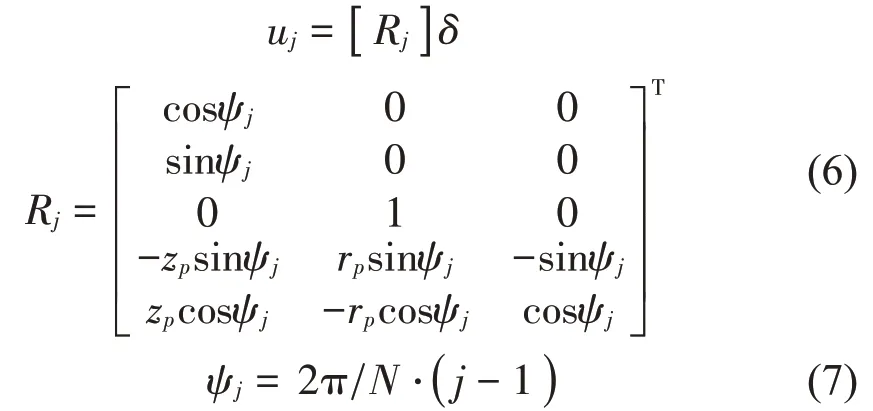
通过上述变换，将滚珠对轴承内圈的作用力转化为滚珠对轴承内圈的整体作用力。根据文献[5]，可以得到轴承内圈的整体平衡方程。

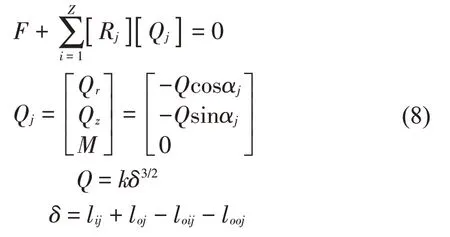
式（8）中的Q表示滚珠与轴承内圈接触所产生的接触力，k表示滚珠与轴承内圈的接触系数，一般情况下是常数，计算方法很多，本文参考文献[13]计算，由上述分析可以得到在受力前后轴承内外圈之间距离的变化，即可以得到轴承与滚珠弹性接触的变形量δ。将式（8）中的平衡方程进行展开，可以得到5个方向的平衡方程表达式，如式（9）所示。

1.2 角接触球轴承的模型求解

由于本文研究的是轴承静态特性，所以不需要考虑角接触球轴承中滚珠的转动。该模型求解的关键是上述5个方向的平衡方程，可以看出上述方程为非线性方程组。本文采用牛顿迭代法进行非线性方程组的求解，设置迭代收敛精度为10-8mm，设置最大迭代步数为1 000步，给出的程序求解流程图如图5所示。

图4 径向剖视图

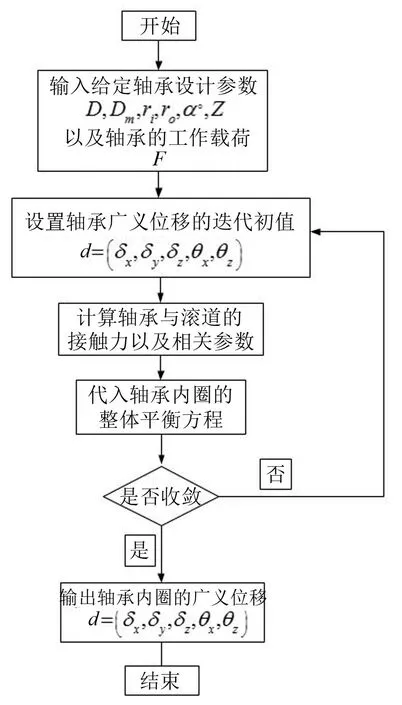
图5 模型求解程序流程图

流程图中的收敛是指通过平衡方程迭代得到位移值与上一次迭代位移值的差值小于事先设定的迭代精度，即差值要小于10-8mm。编程过程中，要注意判断变形量的正负号，滚珠与轴承内圈弹性接触只会产生压缩变形，不会产生拉伸变形，即变形量δ一定是非负的，如果求得的变形量小于零，需要将变形量强制为零进行接下来的迭代计算，这样才能保证程序快速收敛。角接触球轴承的静态刚度最能反映轴承的静态特性。所谓的静态特性分析主要是研究轴承的静态刚度。下面是计算轴承静态刚度的定义表达式。

除了利用定义式求解以外，也可以根据文献[5]采用下列公式进行计算。

2 算例分析

2.1 模型验证

为了验证本文在MATLAB软件中编程的正确性，在给定工况下，采用本方法求解轴承位移和刚度，与已知文献结果进行对比，证明本文模型的准确性、稳定性和通用性。

首先进行轴承位移的对比验证，轴承型号为7128B；滚动体和套圈的材料均为轴承钢，弹性模量E和泊松比ν分别是2.07×105和0.3；载荷工况为Fx=-18 000 N，Fy=0 N，Fz=18 000 N，Mx=0 N·m，My=89 N·m。轴承的具体参数参考表1。

表1 7128B的结构参数

轴承位移的对比结果如表2所示。从表2可以看出，尽管本文模型结果与文献[14]和文献[15]结果存在一定的差异，但数值基本保持一致。上述差异产生的主要原因是因为模型迭代求解精度的不同和弹性接触系数计算方法的不同。同时指出，本文方法中x方向的位移分量δx与文献结果的符号相反是因为本文坐标系x轴与文献坐标系x轴的正方向相反。这一点可以通过x方向施加的载荷看出，即Fx=-18 000 N。

表2 轴承位移结果对比

紧接着进行轴承刚度的对比验证，即采用本方法求解角接触轴承在给定载荷工况下的静态刚度矩阵与文献中实验得到的整体静态刚度矩阵进行对比。轴承型号为RPF7039；轴承的材料参数E=2.07×105，ν=0.3；载荷工况为Fx=Fy=500 N，Fz=2 000 N，Mx=My=1 N·m。轴承的具体参数参考表3。

表3 RPF7039的结构参数

在轴承静态刚度矩阵中，只有对角刚度矩阵才会对轴承的静态特性具有较大的影响。为了简化对比结果，本文仅进行对角刚度矩阵的对比。对比结果如表4所示，本文结果和文献[16]结果分别与文献[17]实验结果进行对比。从对比结果不难看出，本文模型不仅具有准确性和有效性，同时还具备较高的求解精度。同时指出，本文模型与文献实验结果存在差异化的原因可以归咎于模型迭代求解的精度以及本文模型自身的局限性。模型的局限性是指因为本文模型理论本身的局限性。

根据上述轴承位移和静态刚度的对比验证，可以看出本文模型具有准确性、稳定性和通用性。紧接着，在上述模型的基础上对轴承静态特性开展参数化研究，角接触球轴承的静态参数主要包括静态接触角、静态接触力和静态刚度（径向刚度、轴向刚度和角刚度）。同时指出，参数化研究的轴承型号是7128B；材料参数是E=2.07×105和ν=0.3；其余参数见表1。

2.2 轴承外载荷对静态接触角的影响

静态接触角是角接触球轴承的静态参数之一，表示轴承在静止状态下，轴承内外圈与滚动体之间的接触角。由于滚动体处于静止状态，不会产生离心力和陀螺力矩，所以轴承内外圈接触角基本保持一致。所以本节研究的接触角即是指内圈接触角又指外圈接触角。本节首先在不同轴向力作用下研究径向力对角接触球轴承静态接触角的影响，结果如图6所示。同时指出，径向力选取Fx和Fy同步变化；Mx和My均为0。

从图6中不难看出，在纯轴向力作用下，角接触球轴承的静态接触角随着方位角的增加保持不变，且静态接触角随着轴向力的增加而基本保持不变；在给定轴向力和径向力作用下，角接触球轴承静态接触角随着方位角的增加呈正余弦规律变化；在给定轴向力作用下，特殊方位角位置的静态接触角不随径向力的改变而改变，该位置被称作“节点”；同时指出，径向力越大，静态接触角的变化幅度越大。综上所述，可以看出径向力对角接触球轴承静态接触角产生重要影响。

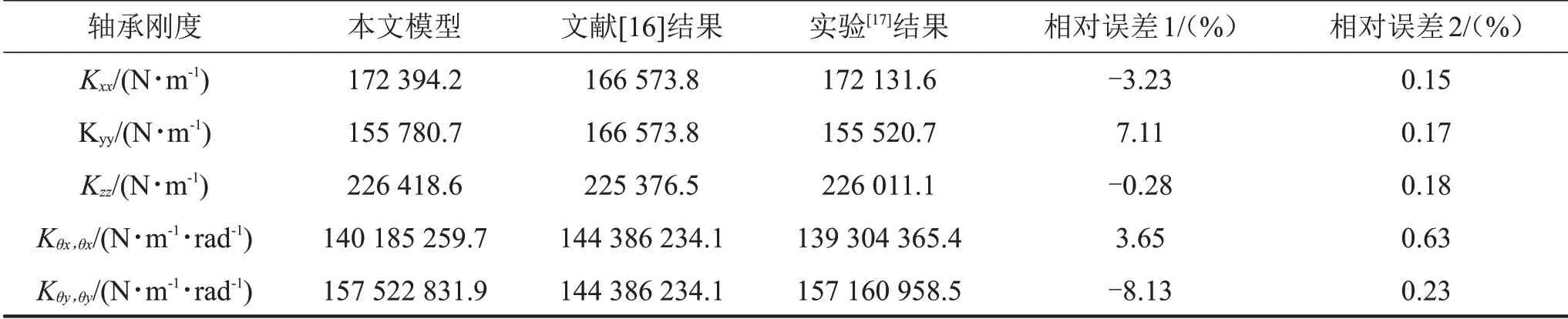
表4 角接触球轴承整体静态刚度对比

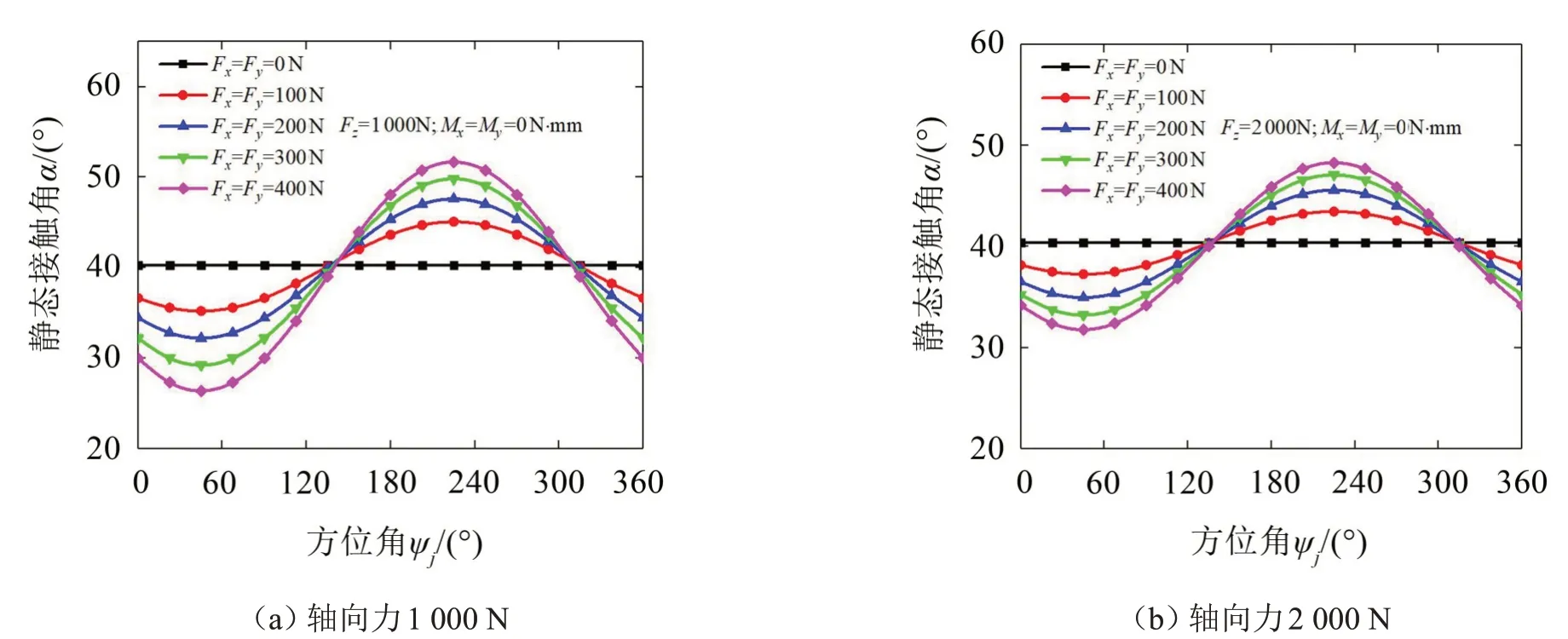
图6 径向力对静态接触角的影响

紧接着，在不同轴向力作用下研究力矩对角接触球轴承静态接触力的影响，结果如图7所示。同时指出，径向力选取Fx和Fy均为0；Mx和My同步变化。

从图7中不难看出，在给定轴向力和力矩作用下，角接触球轴承静态接触角随着方位角的增加呈正余弦规律变化。同时指出静态接触角的变化幅度随着径向力的增加而增加，但变化幅度较小。在给定轴向力作用下，静态接触角在特殊方位角位置也会出现相应的“节点”。综上所述，可以看出力矩对角接触球轴承静态接触角的影响较小，但不能忽视。

图7 力矩对静态接触角的影响

2.3 轴承外载荷对静态接触力的影响

静态接触力是角接触球轴承的静态参数之一，静态接触力表示轴承内外圈与滚动体之间的接触载荷。当轴承处于静止状态时，轴承内外圈静态接触力相同。本节首先在轴向力作用下研究径向力对角接触球轴承静态接触力的影响，结果如图8所示。

从图8中不难看出，在纯轴向力作用下，角接触球轴承静态接触力随轴向力的增加而增加。在给定轴向力和径向力作用下，角接触球轴承静态接触力随着方位角的增加呈正余弦衰减性变化，且静态接触力的变化幅值随着径向力的增加而增加。同时指出，静态接触力在特殊方位角位置会出现“节点”。在给定轴向力作用下，随着径向力的增加，特殊方位角会出现接触角为零的现象，但是这种现象会伴随着轴向力的增加而消失。综上所述，可以得到轴向力和径向力均会对静态接触力产生重要影响。同时指出，轴承在施加外载荷时，应当注意施加径向载荷的大小，不能过大，否则会引起失衡，出现特殊方位角位置接触力为零的现象。

图8 径向力对静态接触力的影响

紧接着，在轴向力作用下研究力矩对角接触球轴承静态接触力的影响，结果如图9所示。从图9中不难看出，在给定轴向力和力矩作用下，角接触球轴承静态接触力随着方位角的增加呈正余弦规律变化，静态接触力在特殊方位角位置会出现“节点”。同时指出，在给定轴向力作用下，静态接触力的变化幅度随着力矩的增加而增加，但是幅值的变化量较小。由此可见，力矩对角接触球轴承静态接触力的影响较小，但对高精度轴承来说不能忽视。

图9 力矩对静态接触力的影响

2.4 轴承外载荷对静态刚度的影响

静态刚度是描述角接触球轴承静态特性的参数之一，轴承静态刚度主要包括径向刚度、轴向刚度和角刚度。这3个刚度对角接触球轴承的静态特性影响最大，本节仅讨论这3个刚度。首先，在轴向力作用下研究径向力对角接触球轴承静态刚度的影响，结果如图10所示。同时指出，由于径向力Fx和Fy同步变化，力矩Mx和My同步变化，所以径向刚度Kxx和Kyy相等，角刚度Kθx,θx和Kθx,θx相等。

从图10中不难看出，对于径向刚度来说，在给定径向力作用下，径向刚度随着轴向力的增加而增加。在给定轴向力作用下，径向刚度随着径向力的增加出现先增加后减少的现象。产生上述现象的原因是径向刚度随着径向力的增加而增加，径向力过大，会导致轴承产生不平衡现象，径向刚度会出现弱化现象。一旦增加轴向力，会减缓弱化现象；对于轴向刚度来说，在给定径向力作用下，轴向刚度随着轴向力的增加而增加。在给定轴向力作用下，轴向刚随着径向力的增加而减小，说明径向力会弱化轴向刚度；对于角刚度来说，在给定径向力作用下，角刚度随着轴向力的增加而增加。在给定轴向力作用下，角刚度随着径向力的增加而减少。这说明径向力会弱化角刚度。综上所述，轴向力会强化轴承静态刚度（径向刚度、轴向刚度和角刚度），径向刚度会弱化轴向刚度和角刚度，但是会强化径向刚度。

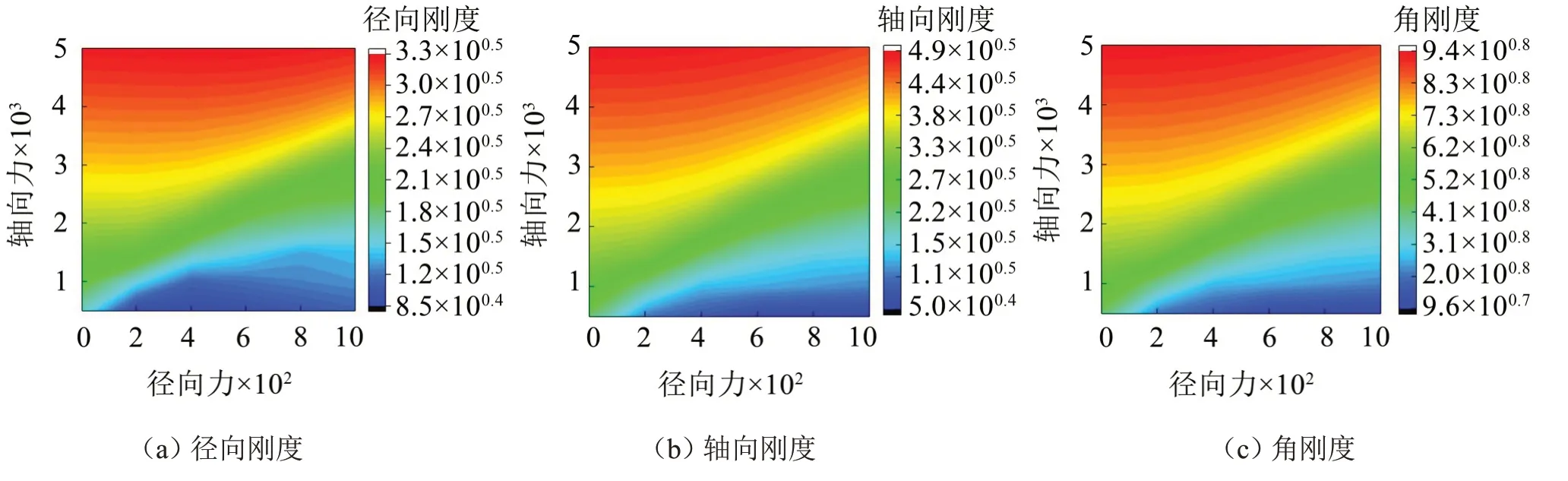
图10 轴向力和径向力对静态刚度的影响

紧接着，在轴向力作用下研究力矩对角接触球轴承静态刚度的影响，结果如图11所示。

从图11中不难看出，在给定轴向力作用下，轴承静态刚度随着力矩的增加而基本保持不变。由此可见，力矩的变化对角接触球轴承静态刚度（径向刚度、轴向刚度和角刚度）几乎不产生影响。

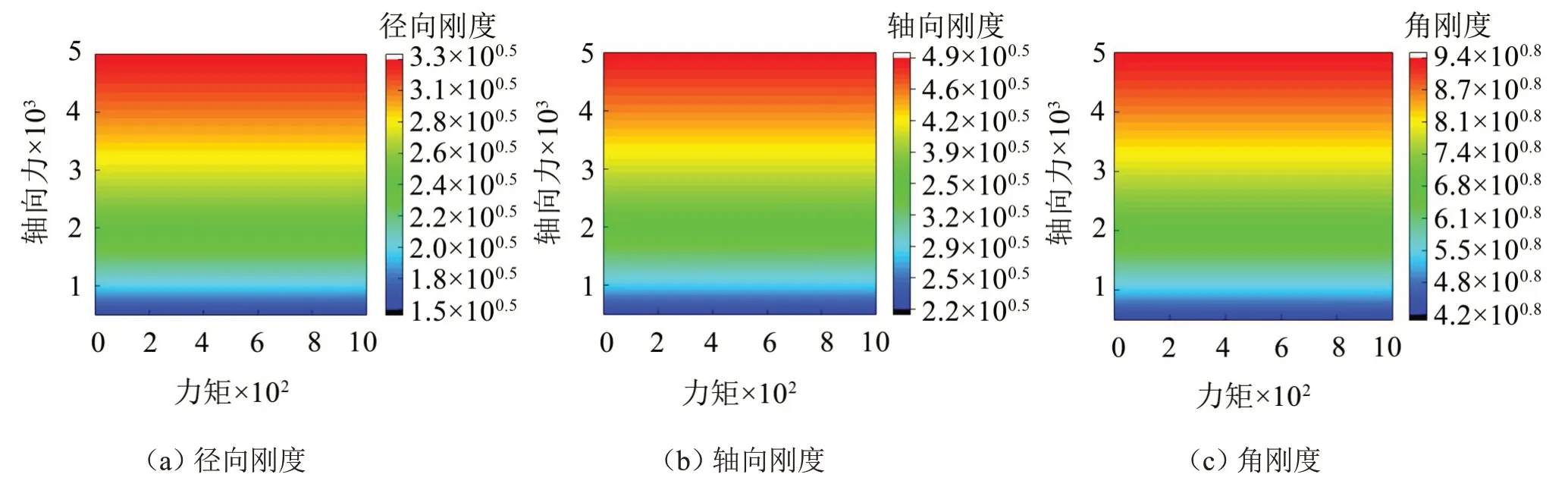
图11 轴向力和力矩对静态刚度的影响

3 结语

（1）基于Demul理论和弹性赫兹理论，建立5自由度角接触球轴承的静态特性分析模型，并利用MATLAB软件采用牛顿迭代法对模型进行求解，与已有文献的实验结果进行对比，证明本模型具有准确性、稳定性和通用性。

（2）根据上述模型，分别研究了轴向力、径向力和力矩作用下对轴承静态接触角和接触力的影响，轴向力和径向力会对静态接触角和接触力产生较大的影响，会出现“节点”，力矩对静态接触角和接触力几乎不产生影响。

（3）根据已建立模型，分别研究轴向力、径向力和力矩对轴承静态刚度的影响，可以看出，轴向力和径向力对轴承静态刚度（径向、轴向和角刚度）产生重要影响，但力矩对轴承静态刚度几乎不产生影响。