含有对称间隙的2自由度振动系统电路仿真

常逢亮，汪诤，胡国静

（兰州交通大学 机电工程学院，兰州 730070）

非光滑机械系统具有复杂的动力学特性，其非线性特性由分段线性、间隙、干摩擦和时滞等非线性因素引起。对于含有间隙的分段线性机械振动系统，当振子在间歇内运动时为线性系统，而一旦接触到边界时，系统将出现弹性系数的突变，造成强烈的振动和噪声，促使机械零件加速磨损和冲击，引起的随机性载荷严重影响到机械零件的寿命和可靠性[1-2]。

非线性机械振动的研究是近年来研究的热点，其以理论研究和数值仿真为手段进行分析。数值仿真采用MATLAB、Fortran或C等编程语言实现，通过长时间的计算获得分岔图和相图。由于数值仿真应用了数值迭代求解微分和积分方程，当精度要求很高时，计算需要花费漫长的时间和巨大的计算量[3]。为了能够快速完成计算过程，研究者通常对算法进行优化，提高数值计算的效率，或采用昂贵的高性能计算机，以期缩短计算时长。

本论文建立了2自由度线性系统的传递函数，确定了非线性特征发生的频率范围。以Multisim为仿真软件，设计了与数学模型完全等效的电子电路模型，该等效电路模型仅由几个TL074CN运算放大器和电阻电容组成，通过仿真得到非线性动力学中相图，不仅极大地降低了对于算法和编程能力的要求，而且电路图具有能直观表达方程式的优点，同时Multisim具有运行时间短和调整参数简便的优点。

1 对称间隙的2自由度振动系统模型

1.1 动力学模型和数值仿真

典型的含有对称间隙2自由度振动系统的动力学模型如图1所示，质量M2通过线性弹簧K2和线性阻尼C2与机架连接，并且在简谐激励P2sin(ωt+τ)的作用下运动。质量M1通过线性弹簧K1和线性阻尼C1与质量M2连接，在距离质量M1零点（M1和M2在受力为0的平衡点）B的两端有线性弹簧K0。设在静态情况下M1和M2所在位置为x1和x2。当质量M1的位移小于对称间隙B时，M1和M2为一个2自由度线性振动系统，当质量M1的位移大于+B或-B时，其与线性弹簧K0接触并发生作用，此时M1受到分段线性弹簧力的作用，并且产生非线性运动。

图1 动力学模型

根据动力学理论，可以建立质量M1和M2的物理方程：

式中非线性部分为

式(1)为物理方程，其每个因子均含有量纲，为了分析方便，将式(1)转换为无量纲方程，取无量纲化参数为

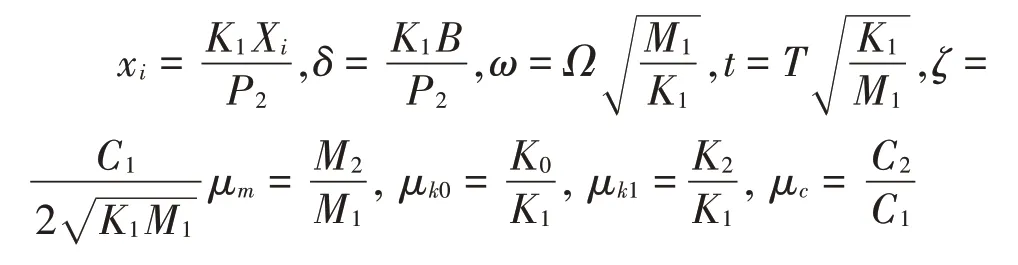
则可得到方程的无量纲化形式，即数学方程为

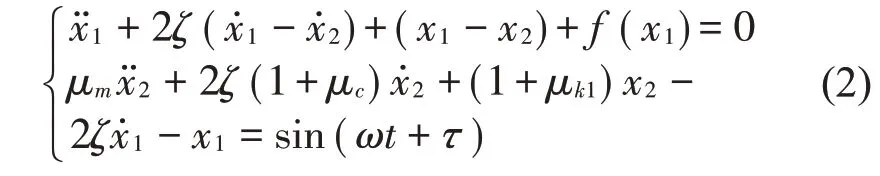
非线性部分为

式(2)中的系数有5个，随着变量ω的变化，系统的运动特性将呈现复杂的运动特征。选取μm=μc=μk1=1，μk0=25，ζ=0.2，δ=0.2，首先确定质量M1与线性弹簧K0不发生接触的频率范围。此时，系统为一个线性系统，将式(2)中的非线性项去掉，即可得到线性方程为

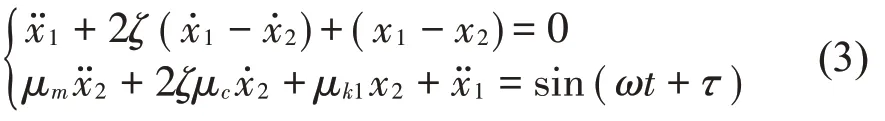
根据动力学模型，对于质量M1，输入可以认为是X2，输出为X1；对于质量M2，输入为激励信号sin(ωt+τ)，输出为X2；而整个系统的输入为激励信号sin(ωt+τ)，输出为X1，建立式(3)的第一个方程的传递函数，有：

则：

建立式(3)的第二个方程的传递函数，有：

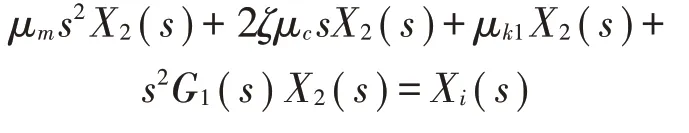
则：

以系统激励信号为输入信号，输出为X1(s)，则系统的传递函数为

则：

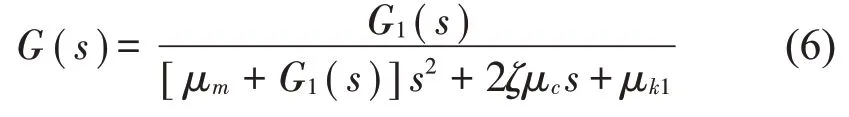
将μm=μc=μk1=1,μk0=25,ζ=0.2,δ=0.2代入式(6)中可以得到：

在Simulink中绘制系统的伯德图，如图2所示。可以看出，系统在频率为1.9附近增益为0.2（纵坐标最小值设为0.2），随后继续下降，因此，系统只有在频率低于1.9时才可能与线性弹簧K0发生接触碰撞。图中横坐标为频率，纵坐标为增益。

1.2 分岔图和相图

根据上述分析，并根据图2和式(7)，可知当μm=μc=μk1=1,μk0=25,ζ=0.2,δ=0.2时，系统中质量M1仅在激振频率小于1.9时才会与线性弹簧K0发生接触并碰撞，系统进入非线性运行范围，而在频率高于1.9时，系统整体呈现线性状态。将参数代入式(2)，令对方程进行状态转换，转换为1阶微分方程，即状态方程为

图2 伯德图

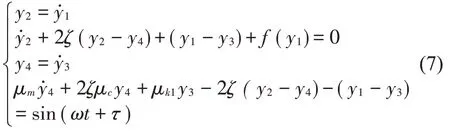
式(7)中非线性部分f(y1)为

根据状态方程式(7)，经过编程绘制分岔图，如图3所示。图中横坐标为频率ω，纵坐标均为相对速度y2-y4。

从分岔图3中可以看出，随着频率ω的变化，含有间隙的2自由度振动系统随着激励频率的变化，系统出现了单周期、2周期、4周期和混沌等复杂的非线性运动特征。根据分岔图，选取图3中的1.35、1.395、1.4、1.44，如图4所示。图中横坐标为M1相对M2的位移y1-y3，纵坐标为M1相对M2的速度y2-y4。

图3 分岔图

2 电路仿真

使用等效电路实现振动系统的分析，首先要将振动系统的方程转换成等效的电路方程[4-7]，将式（7）转换为积分形式：

图4 相图

非线性部分为

在此选择有源积分电路，将式（8）转换成等效的电路方程即：

非线性部分为

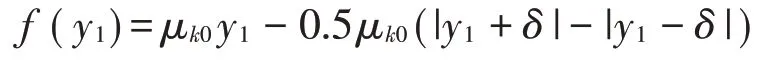
分别选用4个积分模块来实现式(9)，其中运算放大器选用TL074CN，电路设计图如图5所示。其中第一个方程由U1A和U1B实现；第二个方程由U2C、U4B和U4C组成；第三个方程由U1C和U1D组成；第四个方程由U3A、U3B、U3C组成，U4A和U2A为反相器，非线性函数由软件提供的NONLINEAR-DEPENDENT模块实现，供电电压选择±18 V，将式（9）转换为2阶微分方程[8-9]，则有：

式(10)和式(1)形式上完全相同，为了使两式实现等效，必须确定式(10)中各个参数的数值。根据无量纲化过程选取的参数，即μm=μc=μk1=1，μk0=25，ζ=0.2，δ=0.2.考虑到电阻电容的影响，选取R1=R2=10 kΩ，R10=100 kΩ，C1=C2=C3=C4=22 nf，则得到R4=R7=30 kΩ，R5=R9=30 kΩ，R3=R6=R8=43.3 kΩ，其余电阻仅用于反相电路，所以均取100 kΩ。

图5 电路图

正弦波函数的幅值可由δ=0.2求得：

δ=0.2，即可得Vm=1.067 V

由无量纲化过程，可得出激励频率f和ω之间的关系为

3 Multisim12.0仿真

通过MultiSim12.0对电路模型进行仿真，函数发生器正弦波幅值为1.067 V，选择激励频率分别为563.86 Hz(1.35ω)、582.65 Hz(1.395ω)、584.74 Hz(1.4ω)、601.45 Hz(1.44ω)，运行结果如图6所示。示波器中横坐标通道1为位移(y1-y3)，刻度为100 mV/Div；纵坐标通道2为速度(y2-y4)，刻度为100 mV/Div。

图6 电路仿真相图

相比较于通过编程绘制相图，Multisim12.0绘制的相图和其完全一样。自行编程的运行时间为等效电路仿真的3倍，说明了程序需要进行更进一步的优化，当然更说明了编程对于非线性研究的影响太大，能降低其影响，可以提高研究效率。同时电路仿真还拥有着动态参数可调的优点，利用等效电路分析非线性动力学，降低对编程要求，提高研究的效率。

4 结语

通过对2自由度线性系统建立传递函数，应用bode图分析分段线性系统的碰撞区间，确定分段线性动力学系统发生非线性特性的频率范围，减少数值分析的计算时长。应用Multisim12.0电路仿真软件中的NONLINEAR-DEPENDENT模块及几个TL074CN运算放大器、电阻电容等简单的电路元器件，快速建立与动力学模型等效的电路模型，得到与数值仿真相同的结果。由此可见等效电路可以实现非线性动力学的分析和研究，节省了数值仿真对算法、编程和计算机性能的要求，为非线性动力学研究提供了一种很好的研究方法。