含Dankowicz动摩擦的碰撞振动系统动力学分析
张艳龙,魏超,王丽,王振禄
(1.兰州交通大学 机电工程学院,兰州 730070;2.兰州城市学院 数学学院,兰州 730030)
众多机械系统运行过程中构件之间都会产生摩擦,如轴承、抗蛇形减震器、齿轮、机器人关节等。在机械系统运行过程中,因摩擦及间隙导致的振动不仅影响系统性能,也导致零件磨损失效,产生噪声,甚至发生不安全的事故。因此,对引入摩擦的强非线性碰撞振动系统,有许多学者构建得到了一些力学模型和摩擦模型,研究因摩擦作用出现的系统粘滑、颤振等动力学现象。Cone等[1]将冲击振荡器模型简化,分析含摩擦的振动系统行为,发现存在多种不同的分岔行为。钱大帅等[2]和Fang等[3]研究一种具有库伦干摩擦的振动系统,分析系统粘滑运动边界,并解释了滑移、黏滞等运动状态之间的转换。Shaw[4]研究在简谐激励的作用下,一类分段线性系统的运动稳定性,研究发现了系统存在复杂的摩擦诱导振动现象及多种分岔特性。丁旺才等[5]、朱喜锋等[6]和Pascal[7]数值模拟得出系统因摩擦诱导粘滑振动行为,并发现系统的颤碰运动现象。Awrejcewicz等[8-9]理论分类探讨含摩擦的振动系统在自激励与外激励分别作用的情况下,系统发生粘滑与混沌运动交替出现的动力学现象,并利用数值模拟得出系统的运动过程。乐源[10]简化得到了一种存在摩擦振动的物理模型,研究了系统在Neimark-Sakerpitchfork分岔点附近的双参动力学行为。
随着学者的研究深入,静摩擦模型已经不能更加准确描述内部变量对摩擦振动系统的影响,部分学者开始深入微观,建立自身包含动力学性质的动摩擦模型,如:Dahl摩擦模型、LuGre摩擦模型、Dankowicz摩擦模型等。Pikunov等[11]和Ashesh等[12]分别针对含LuGre动摩擦和Dankowicz动摩擦的非光滑机械系统,进行系统稳定性分析,对比在不同参数影响下的系统运动情况。Hoffmann[13]研究了LuGre动摩擦模型对摩擦振动系统点接触稳定滑动基本机理的影响。张艳龙等[14]建立一类含Dankowicz动摩擦单自由度振动系统,分析得出振子受力的判断条件,并研究了摩擦导致系统振动和两种参数影响下系统呈现的动力学行为。本文在文献[14]的基础上,引入Dankowicz动摩擦对轴承系统进行简化,得到一类含动摩擦的2自由度碰撞振动系统动力学模型,分析了系统在不同阶段的运动过程及条件,并数值仿真了一些非常规分岔行为及系统参数变化对系统动力学行为的影响,从而为轴承运动的稳定性、安全性及系统结构优化提供一些理论参考依据。
1 力学模型
单列圆柱滚子轴承的结构如图1所示。

图1 单列圆柱滚子轴承的结构示意图
在实际有关轴承的机械系统中,随着机械系统的高速运转,圆柱滚子将会与保持架两端发生碰撞,同时保持架与轴承内圈发生摩擦振动。为了深入得到轴承在机械系统运转过程中呈现的动力学行为,将单列圆柱滚子轴承简化为一类含动摩擦的碰撞振动系统力学模型如图2所示。其中,将轴承的内圈简化为传送带,圆柱滚子简化为质量M1的振子,保持架简化为质量M2的振子,将两振子之间润滑油简化为刚度系数为K1和K2的线性弹簧及阻尼系数为C1和C2的线性阻尼器,轴承外圈简化为固定壁,振子M2与固定壁之间润滑油简化为刚度系数为K3的线性弹簧,两振子之间接触面均为光滑表面,振子M2与传送带之间为粗糙表面,Vb为传送带速度,振子M1在水平方向上由间隙为2D的两个挡块进行约束,假设阻尼是Rayleigh型比例阻尼,碰撞过程由碰撞恢复系数R确定,简谐激振力Psin(ΩT+τ)作用在振子M1上,振子M1与振子M2的位移分别用X1和X2表示。

图2 含动摩擦的碰撞振动系统力学模型
Ff为带与振子M2之间作用的摩擦力,该摩擦力的表达式为[12]
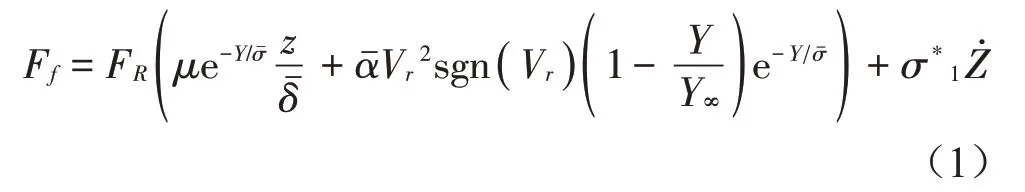
式(1)右边前半部分表示切向方向的等价微凸体形变,后半部分表示两个接触面之间的分离距离,FR是法向载荷总和,μ是摩擦系数是粗糙度高度的标准差是最大的允许微凸体形变,Vr=Vb-是带与质块的相对滑移速度,Y∞是将微凸体半径转换为法向的分离距离,动摩擦模型的内部变量Z由方程式(2)支配[12]:

式中,对于Vr>0,Z趋向于;对于Vr<0,Z趋向于-故Z∈[-]。
状态变量Y的运动由方程式(3)支配[12]:

取无量纲参数及变量为

系统运动的无量纲微分方程(4)为

当|x1-x2|=d时,振子M1与振子M2发生碰撞,碰撞前后速度关系无量纲表达式(5)为
将高岭土浆料于110 ℃烘干3 h,然后粉碎、研磨,置于马弗炉500 ℃煅烧 2 h,即得煅烧高岭土粉体.将煅烧高岭土粉按一定比例掺入低碳混凝土中代替部分矿粉,并与基准组进行比较,探讨其对低碳混凝土性能的影响.依照GB/T 50081-2002《普通混凝土力学性能试验方法》和GB/T 50082-2009《普通混凝土长期耐久性能试验方法》对所制备的低碳混凝土的物理性能、强度及耐久性能进行检测.
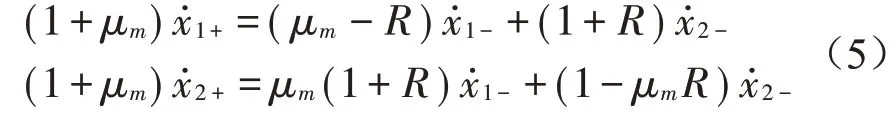
式中:标注符号“-”和“+”分别表示振子M1与振子M2发生碰撞前和碰撞后的状态。
Dankowicz动摩擦模型无量纲表达式(6)为

式中:


为了全面清楚研究得到的系统运动状态变化,分析两个振子的受力及速度变化,将系统运动过程分类讨论如下:
过程1:由于振子M1在简谐激振力作用下始终处于运动状态,对振子M2进行系统受力分析,令F2表示振子M2所受到的合力,则F2=2ξ(1+μc1)×若振子M2合力大于或等于零且振子M2的速度不为零,即F2≥0,≠0时,振子M2做加速滑移运动,两振子都处于运动状态;若振子M2合力小于零且振子M2的速度不为零,即F2<0,≠0时,振子M2做减速滑移运动,两振子都处于运动状态。
过程2:同上振子M1始终为运动状态,F2表示振子M2的合力,若振子M2合力小于零且振子M2的速度大小等于带速,即时,振子M2处于粘着状态。
过程3:因振子M2受合外力F2的影响,当两振子的位移差|x1-x2|=d时,振子M1与振子M2发生碰撞。
为了准确描述摩擦诱导振动特性,揭示摩擦振动现象,用符号n-p-q表示系统的运动状态,其中:n表示激励周期数;p、q分别表示振子M1与振子M2在右侧和左侧挡块的碰撞次数。为了准确描述系统相轨线与碰撞面关系及系统分岔特性,选取Poincaré截面建立Poincaré映射X(i+1)=其中:为实参数。
2 激振频率ω对系统的影响

图3 系统运动分岔图

图4 投影Poincaré映射图
由于分岔图不能显示系统的擦边碰撞、粘滑运动等行为,系统运动相图如图5所示。当选取ω=2.908时,如图5(a)显示系统进入周期3-6-9运动,系统经Grazing分岔出现左侧擦边碰撞行为,此时由于振子M1与振子M2运动位移差恰好为-d时,振子M2的合力方向突然改变,振子M2在合力作用下远离挡块运动,发生振子与左侧挡块擦切。当选取ω=2.981时,如图5(b)显示系统进入周期3-6-8运动,随着ω增大,系统出现Bare-grazing分岔,即系统发生擦边碰撞,导致周期运动失稳,随即转迁为混沌运动。当选取ω=4.145时,如图5(c)显示系统进入周期4-7-6运动,系统经Grazing分岔出现右侧擦边碰撞行为,此时由于振子M1与振子M2运动位移差恰好为d时,振子M2的合力方向突然改变,振子M2在合力作用下远离挡块运动,发生振子与右侧挡块擦切。当选取ω=5.569时,如图5(d)显示系统进入周期1-1-2运动,随着ω逐渐变大,系统进入稳定的周期1运动。
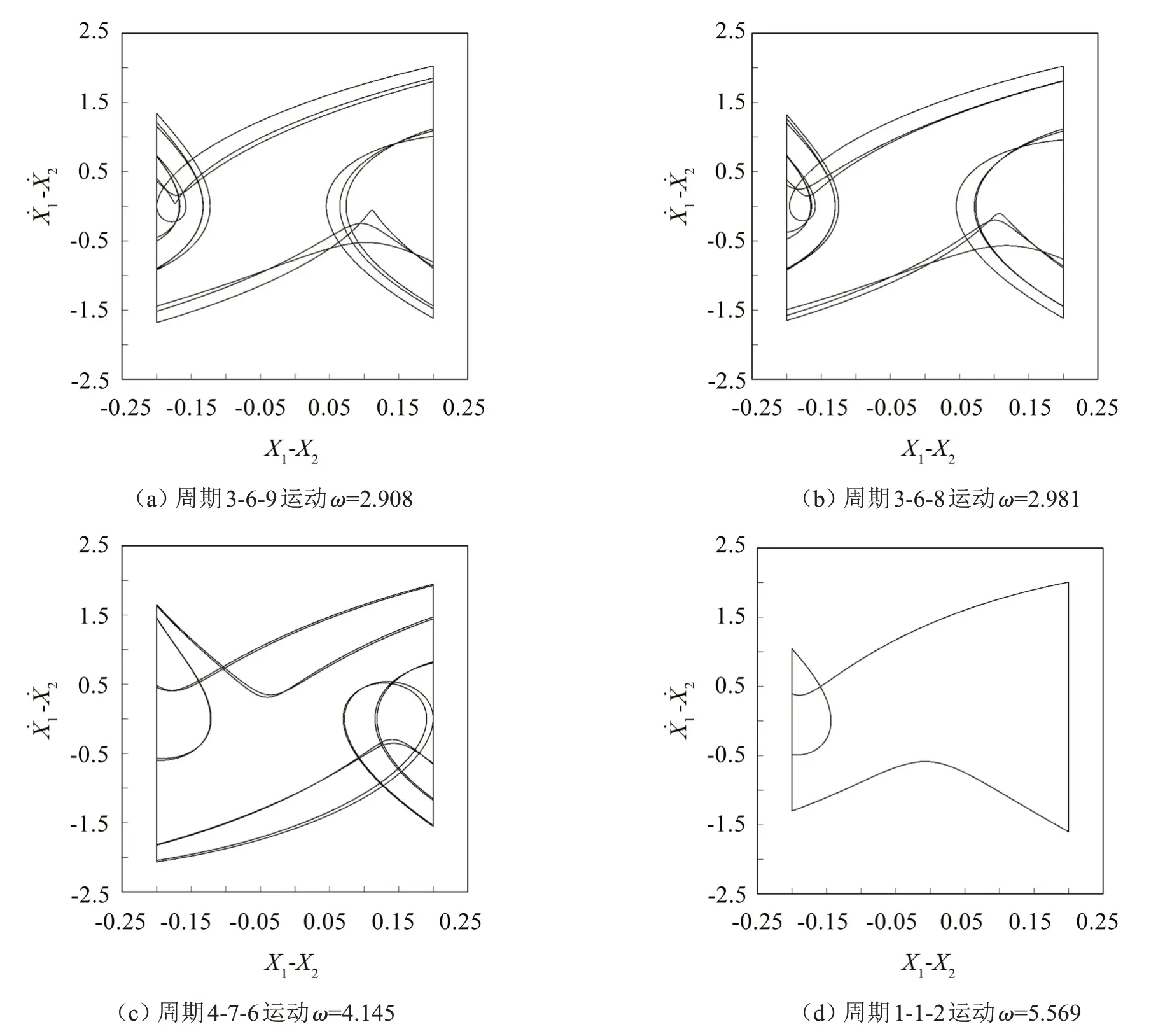
图5 系统运动相图
3 间隙d对系统的影响
经过大量数据仿真实验,发现不同系统参数下系统的动力学行为不同,为了能够更好地表达d影响下系统摩擦诱导粘滑碰撞振动特性,选取如下特例参数:
μc1=0.1,μk1=0.2,μk3=0.6,ξ=0.1,μm=0.4,μ=0.2,α=2.2,vb=0.2,R=0.8,σ=0.01,fr=3,δ=0.000 1,σ1=10,γ=3000,y∞=2 000。
以间隙d作为分岔控制参数,研究间隙d影响下系统呈现的动力学行为。选取几种不同的较低激振频率,数值模拟呈现出间隙对系统摩擦诱导振动响应的系统运动分岔图如图6所示。当选取ω=3.0时,如图6(a)为系统运动分岔图,随着间隙的变化,系统表现为周期与混沌运动相互转迁的复杂特性,系统混沌窗口较宽。当选取ω=3.5时,如图6(b)为系统运动分岔图,相比ω=3.0时,系统清晰表现经周期倍化分岔进入混沌,但系统存在多种分岔行为,混沌窗口依然较宽。当选取ω=3.8时,如图6(c)为系统运动分岔图,系统主要发生周期倍化分岔等常规分岔行为,系统混沌窗口略微变窄。选取不同的较高激振频率,数值模拟呈现出间隙对系统摩擦诱导振动响应的系统运动分岔图如图7所示。当选取ω=6.8、7.2、7.5时,系统运动全局分岔图分别如图7(a)、7(b)和7(c)所示,随着间隙的变化,系统主要呈现周期运动,混沌窗口几乎逐渐消失。
选取激振频率ω=3.5,间隙影响下系统振动响应如图8所示。如图8(a)为图6(b)的局部放大图。当d=0.225时,如图8(b)显示系统处于稳定周期1运动,随着d逐渐减小,周期运动失稳,发生倍化分岔,如图8(c)显示系统进入稳定周期2运动。随着d继续减小,系统发生Neimark-Sacher分岔进入概周期运动,如图8(d)显示形成两个吸引不变圈。随着d继续减小,系统经过锁相(如图8(e)所示)进入混沌运动。选取d=0.195时,如图8(f)显示系统发生Sliding分岔出现粘着运动。选取d=0.144时,如图8(g)显示系统出现逆Bare-grazing分岔,从混沌运动瞬间进入稳定周期2-4-6运动,随着d减小,系统出现Bare-grazing分岔,即系统发生擦边碰撞,导致周期运动失稳,随即转迁为混沌运动。选取d=0.136 3时,如图8(h)显示系统经Grazing分岔出现左侧擦边碰撞行为,此时由于振子M1与振子M2运动位移差恰好为-d时,振子M2的合力方向突然改变,振子M2在合力作用下远离挡块运动,发生振子与左侧挡块擦切。

图6 低频下系统随间隙变化的分岔图
4 结语
研究一类含动摩擦的碰撞振动系统,对两振子的受力和速度变化情况分类研究,理论分析系统进入不同阶段的运动条件,利用数值仿真分析摩擦诱导碰撞振动系统动力学特性,结果表明:
(1)随着激振频率逐渐变化,系统呈现出周期与混沌运动相互转迁的复杂动力学特性,如系统发生Grazing分岔出现擦边碰撞行为、系统由周期运动经Bare-grazing分岔直接进入混沌运动、系统发生Neimark-Sacher分岔经锁相进入混沌运动。
(2)选取较低激振频率时,随着间隙改变,系统发生Neimark-Sacher分岔、周期倍化分岔、Sliding分岔、Grazing分岔和Bare-grazing分岔等多种分岔行为,呈现出周期与混沌运动相互转迁的复杂动力学特性,系统混沌窗口较宽。当选取较高激振频率时,随着间隙的变化,系统主要呈现周期运动,混沌窗口几乎逐渐消失。
通过理论分析及数值仿真,为含轴承的机械系统在实际的应用中结构参数的优化和系统运动的稳定性改善提供理论参考依据。
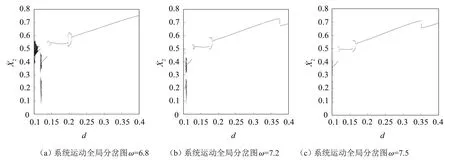
图7 高频下系统随间隙变化的分岔图

图8 间隙影响下系统振动响应(ω=3.5)

图8 间隙影响下系统振动响应(ω=3.5)

