非自由声场中目标声源粒子速度场的重构

周达仁，肖永雄，卢奂采

（浙江工业大学 机械工程学院，杭州 310023）

近场声全息技术[1-3]使用布置在声源近场的全息测量面获取的声场信息，重构出结构表面和三维声场中的声压、介质粒子速度和声强等声学量的分布，为结构噪声源的识别定位提供了强大的技术支撑。近场声全息技术的一般思路是利用齐次Helmholtz方程在各类坐标系下的基本解，即自由空间的格林函数建立结构表面声学量与场点声学量、以及各场点声学量之间的关联，并建立相应的声场模型，再通过求解逆问题，将全息测量面上的声学量映射到重构面。相应地，在具体实施时，声源则必须置于开放的自由声场或全消声的环境中[1]。这一要求使得近场声全息的实施受到一定程度的限制。为了解决这一问题，研究者在各类近场声全息技术的基础上，发展出了相应的声波分离方法[4-18]。

在建立同时包含目标声源和干扰声源辐射的非自由声场数学模型时，声波分离方法使用两组基函数分别对目标声场和干扰声场进行建模。相应地，则需使用两组全息测量值作为算法的输入量，以求解出两组基函数系数。常用的测量前端有双层声压测量面[4-8]、双层粒子速度测量面[9-11]或者单层声压-粒子速度联合测量面[7-8,11-15]。也有研究者使用单层声压测量面[16-18]作为测量前端，重构目标声源的声压场，在特定的声场模型下，获得了较高的重构精度。

在对非自由声场中目标声源辐射重构的研究中，所重构的声学量多为声压标量，而对介质粒子速度矢量的重构则相对较少。相对于声压场，粒子速度场包含了更为丰富的声场信息。然而，粒子速度重构的传递矩阵的病态性也更大[19]。因此，对粒子速度的重构相比于对声压的重构更具有挑战性。Jacobsen等[8,11]以统计最优近场声全息技术为基础，对非自由声场中目标声源的粒子速度场进行了重构，并对比了以双层声压测量面、双层粒子速度测量面和单层声压-粒子速度联合测量面作为测量前端时的重构精度。Langrenne等[15]提出了基于逆边界元法的声波分离方法，对置于刚性反射边界附近的目标声源的粒子速度场进行了重构。Hu等[6,9-10,12]基于等效源法，对目标声源的粒子速度场进行了重构，并对比了双层声压测量面和双层粒子速度测量面得到的重构结果[9-10]。基于傅里叶声学法，Hu等[4]对非自由声场中平面声源辐射的粒子速度场进行了重构。

基于球面波函数叠加的近场声全息方法所使用的全息测量面可以为不规则的、非封闭的几何形状，相比于傅里叶声学法、统计最优法和逆边界元法，其实施更为灵活[1,19]。另外，随着P-U探头[20]技术的不断发展，在实施全息测量时，直接获取声场中的粒子速度变得容易。因此，本文在基于球面波函数叠加的近场声全息方法的基础上，辅以单层的粒子速度测量面作为前端，对非自由声场中目标声源辐射的粒子速度场进行重构。

本文的第1节介绍粒子速度重构的数学模型；第2节通过数值仿真对所提方法加以验证；第3节对所提方法进行消声室内的实验验证；第4节是对全文的总结。

1 数学建模

1.1 自由声场中粒子速度的建模

自由声场中任意场点处的声压可表述为有限项的球面波函数的叠加[19]。当声场为稳态时，忽略时间变量t的相关项e-iωt，其中：i=，ω为声波角频率，场点x的声压p(x;ω)的表达式为

其中：ψj(x;ω)为球面波基函数，cj(ω)为基函数系数，j为基函数项序数，J为基函数总项数。使用球面坐标(r,θ,φ)，ψj(x;ω)可表示为[19]

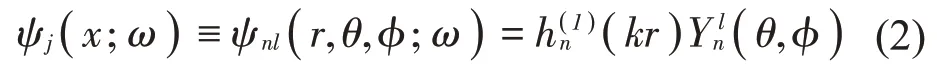
在自由声场中，场点x处的声压p(x;ω)与粒子速度v(x;ω)通过欧拉方程建立联系：

其中：Δ为梯度算子。将式(4)代入式(1)中，可得到场点x处的，在单位法向矢量n方向的粒子速度分量：

若在声场中布置传感器采集一组场点的声压或法向粒子速度，则由式(1)和式(5)分别可得：

其中：C(ω)为基函数系数列向量，m=1,…,M，M为采样点数，声压展开矩阵Ψp(xm;ω)与粒子速度展开矩阵Ψv(xm;ω)满足关系式：

使用包含M个粒子速度测点的全息测量面采集测量面法向的粒子速度分量，通过对式(7)求逆，可求出基函数系数向量：

其中：上标H表示共轭转置。当基函数系数C(ω)求得之后，在声源表面或空间的场点处的法向粒子速度可由下式重构得到：

其中：s=1,…,S，S为重构点数为重构点处的法向粒子速度的展开矩阵。

1.2 非自由声场中粒子速度的重构

如图1所示，当粒子速度测量面另一侧存在干扰声源时，第1.1节中所述的方法不再适用于目标声源的辐射粒子速度场的重构，因为，测量面所处的声场为非自由声场。

图1 目标声源和干扰声源辐射的非自由声场

以目标声源的几何中心O1和干扰声源的几何中心O2为原点建立局部坐标系，在第m个测点处，目标声源和干扰声源的法向粒子速度的贡献可分别表示为

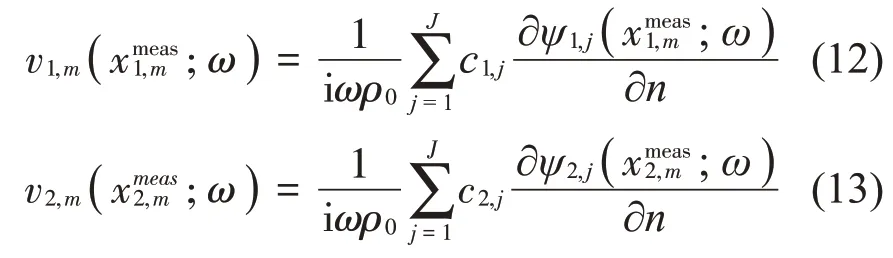
其中：

其中：上标T表示向量的转置。式(15)右边的两叠加项的物理意义分别为源于坐标原点O1和O2的外行波。求解式(14)，可得系数向量为

在求解系数向量之前，需要确定最优展开项数Jopt。将重构的粒子速度与采集的粒子速度进行对比，计算出相对误差的2-范数，遍历不同的展开项数重复上述过程，将最小误差2-范数的对应的展开项数定为最优展开项数Jopt。在数学上，最优项数选取准则可表示为[21]

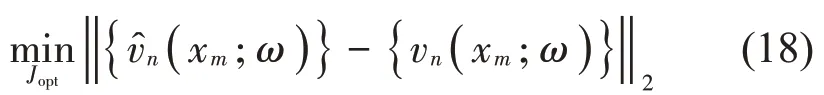
再结合式(11)即可重构出目标声源辐射的粒子速度场。

2 数值仿真

在本节中，选取脉动球、刚性摆动球和点激励简支板，这3类辐射粒子速度场具有解析解的声源，对所提方法进行仿真验证。空气密度和声速分别设为1.29kg/m3和340m/s。为了对重构精度量化评估，定义重构面上的相对重构误差为[16]

2.1 脉动球和刚性摆动球辐射的非自由声场

图2所示为目标声源、干扰声源和粒子速度传感器阵列组成的仿真声场。定义全局坐标系Oxyz以描述两声源和阵列之间的相对位置关系，O1和O2分别为两组球面波函数的局部坐标原点，各自位于两个声源的几何中心。使用脉动球和刚性摆动球分别作为目标声源和干扰声源。脉动球半径为0.05m，球心坐标为(0.06m,0m,0m)，球面质点径向振动速度为0.011m/s。刚性摆动球声源半径为0.05m，球心坐标为(0.06m,0m,0.4m)，球体沿z轴方向摆动速度为0.016m/s。平面粒子速度传感器阵列的孔径为0.2m×0.2m，其上包含36个测点，相邻测点间距为0.04m，使得在频率f=1500Hz时，一个声波波长包含6个测点；阵列面几何中心位于z轴，与x-y平面平行，两者距离为0.1m。为了便于描述重构结果，对36个粒子速度测点编号，如图3所示。

图2 脉动球、刚性摆动球以及粒子速度传感器阵列组成的仿真声场模型

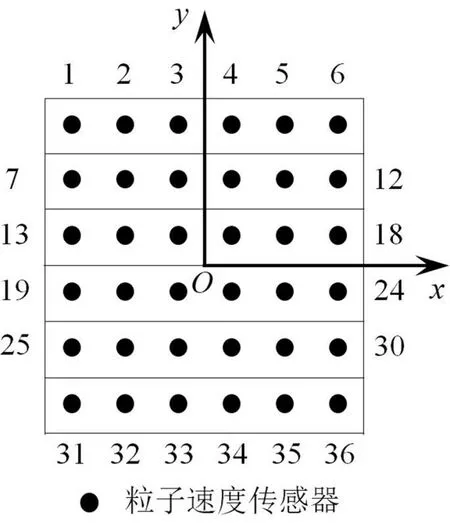
图3 阵列上传感器的分布和编号规则

其中，第1号测点坐标为(-0.1m,0.1m,0.1m)，第36号测点坐标为(0.1m,-0.1m,0.1m)。需要说明的是，平面阵列并非本方法的最优阵列形状。与目标声源几何结构共形或者近似共形的阵列更有利于均匀地采集目标声源的声场信息，得到更高的对目标声源辐射粒子速度的重构精度[17]。然而，在仿真和实验中，均使用平面阵列采集粒子速度信息，目的在于检验所提方法对阵列拓扑结构的鲁棒性。对阵列的测量值施加信噪比为30 dB的高斯白噪声，以模拟测量误差的影响。

使用本文所提方法重构出脉动球辐射在阵列各测点处的法向粒子速度。结果显示，最优展开项数为Jopt=3，相对重构误差为ε=2.54%。图4(a)和图4(b)给出了各测点处的法向粒子速度幅值和相位的分布，包括两声源辐射的叠加值、目标声源辐射的重构值和理论值。从图中可知，由于受到干扰的刚性摆动球辐射的影响，无论是幅值还是相位，两声源的叠加值相对于理论值均存在一定的偏差。使用本文所提出的粒子速度重构方法后，重构值与理论值能够很好地吻合。结果表明，该方法能以很高的精度抑制刚性摆动球辐射的影响，重构出脉动球声源辐射的粒子速度场。

图4 粒子速度在阵列各测点处的分布曲线，包含两声源辐射叠加值、脉动球辐射的重构值和理论值

2.2 刚性摆动球和点激励简支板辐射的非自由声场

在上一算例中，目标声源和干扰声源均为理想的球形声源，使用低阶的球面波函数即可对其辐射声场精确描述，因而获得很高的重构精度。在本算例中，选用刚性摆动球作为目标声源，选用在工程应用中更为常见的板声源作为干扰声源，对该方法进行进一步验证。

仿真声场模型如图5所示。刚性摆动球半径为0.04m，沿z轴方向的摆动速度为0.05m/s，球心O1，即描述其辐射声场的球面波函数的局部坐标系原点的全局坐标为(0.08m,0m,0m)。方形简支板的边长为0.16m，板的振动表面与x-y平面平行，其几何中心位于(0m,0m,0.5m)。板的其它参数为：杨氏模量，2.06×1011Pa；泊松比，0.3；厚度，0.001m；密度，7 850kg/m3。对板施加幅值为25N的简谐激励，施力点坐标为(0.05m,0m,0.5m)，并假定在板所在的平面上，其外部区域为刚性障板，即表面振动速度为零，此时，板表面的速度分布可由模态叠加法计算得到。在得到表面速度分布之后，板辐射粒子速度场可由瑞利第一积分联同欧拉方程计算得到。在本算例中，选取简支板振动的前25阶模态计算其表面速度分布。根据文献[21]，将描述板辐射声场的球面波函数的局部坐标原点O2设置在(0m,0m,0.58m)处。平面粒子速度传感器阵列的孔径、测点数、相邻测点间距以及测点坐标等参数与上一算例相同。对阵列的测量值施加信噪比为30dB的高斯白噪声。

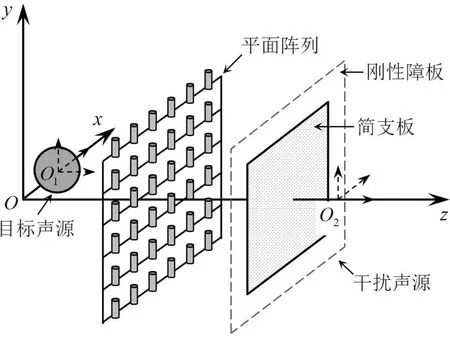
图5 刚性摆动球、简支板以及粒子速度传感器阵列组成的仿真声场模型

使用本文所提方法重构出刚性摆动球声源在阵列各测点处的法向粒子速度。结果显示，最优展开项数为Jopt=12，相对重构误差为ε=14.67%。图6(a)和图6(b)给出了各测点处的法向粒子速度幅值和相位的分布，包括两声源辐射的叠加值、目标声源辐射的重构值和理论值。

从图6(a)中可知，由于受到板声源的辐射的影响，在大多数测点处，两声源叠加的幅值相对于理论值均明显偏大，并且，两者在各测点分布趋势明显不同。使用本文所提出粒子速度重构方法后，重构幅值与理论幅值能够较好地吻合，误差较大的测点多分布在阵列边缘的测点处，因为在使用球面波函数描述板声源声场时，对阵列中心附近场点的描述精度要高于对边缘场点的描述精度。在图6(b)所示的速度相位分布中，也能观察到类似的现象。结果表明，该方法能以一定的精度抑制板辐射的影响，重构出刚性摆动球辐射的粒子速度场。

图6 粒子速度在阵列各测点处的分布曲线，包含两声源辐射叠加值、刚性摆动球辐射的重构值和理论值

3 实验验证

在本底噪声低于18 dB(A)的全消声室中，对本文所提方法进行了实验验证，主要的实验设备布置如图7所示。在实验中，使用两个直径约为0.05m的同型号扬声器作为目标声源和干扰声源，声源纸盆中心坐标分别为(0m,0m,0m)和(0m,0m,0.2m)。使用的粒子速度采集前端为Microflown公司生产的手持式P-U探头阵列。该阵列为平面阵列，孔径为0.225m×0.150m，其上均匀分布12个探头，测点间距为0.075m。阵列面与x-y平面平行，距离为0.05m。对12个测点进行编号，如图8所示。

图7 主要实验设备的布置

图8 阵列上P-U探头的分布和编号规则

在实验数据采集过程中，首先同时驱动两个扬声器以相同频率发声，使用P-U探头阵列采集声场粒子速度，得到粒子速度的叠加值；然后，关闭干扰声源，在相同参数下驱动目标声源发声，采集得到目标声源辐射的理论值。设置第9号测点处采得的声压信号作为参考信号。12个通道采集的粒子速度信号与参考信号进行互功率谱计算，得到各测点法向粒子速度的相位信息；12个通道采集的粒子速度信号进行自功率谱计算，得到各自的幅值信息。然后，将各测点处的法向粒子速度的频域值输入重构算法，对测量面上各测点处的粒子速度进行重构，得到目标声源辐射的重构值。

给出频率为f=1500Hz时的重构结果。当f=1 500Hz时，最优展开项数为Jopt=11，相对重构误差为ε=8.67%。图9(a)和图9(b)给出了各测点处的法向粒子速度幅值和相位的分布，包括两声源辐射的叠加值、目标扬声器声源辐射的重构值和理论值。观察图9发现，由于受到干扰扬声器辐射的影响，两声源的叠加的速度分布远远偏离于目标扬声器辐射的理论分布。使用本文所提出的粒子速度重构方法后，重构值与理论值能够较好地吻合，这说明干扰扬声器声源的辐射所造成的影响被较好地抑制。实验结果验证了本文所提方法在存在干扰声源辐射影响的情况下，对目标声源辐射粒子速度场的重构效果。

图9 粒子速度在阵列各测点处的分布曲线，包含两扬声器辐射叠加值、目标扬声器辐射的重构值和理论值

将实验的重构误差与两个仿真算例的重构误差进行对比分析。第2.1节中以刚性摆动球作为干扰声源时的重构误差最低，第2.2节中以点激励简支板作为干扰声源时的重构误差最高，实验所得的重构误差介于两者之间。这是因为，在所建的声场模型中，以两组球面波扩展函数分别描述目标声源和干扰声源的辐射粒子速度场，从而，该模型对球形声源辐射粒子速度场的描述精度高于对板形声源的描述精度。所以，在仿真算例中，以球形声源作为干扰声源时的重构精度远高于以板形声源作为干扰声源时的重构精度。对于实验而言，一方面，由于扬声器声源辐射声场接近于双极子声场，球面波扩展函数对其辐射声场的描述精度高于对板形声源的描述精度，使得重构误差比第2.2节的重构误差为低；另一方面，实验的声场环境较仿真而言更为复杂，使得重构误差比第2.1节中以理想的球形声源作为干扰声源时的重构误差为高。另外，由于实验所用到的P-U探头阵列为商业化产品，其测点间距、测点个数和测量孔径等参数为固定值，且并非该声场条件下的最优化阵列参数。如果适当减小测点间距、增大测点数目，可以更为充分地采集声场信息，实验有望获得更高的对目标声源辐射粒子速度的重构精度。

4 结语

本文提出了一种基于单层粒子速度测量面作为测量前端的非自由声场中目标声源辐射粒子速度场的重构方法。该方法使用两组球面波扩展函数分别对目标声源和干扰声源的辐射粒子速度场进行建模，以两组基函数的线性叠加来匹配全息测量面上测得的粒子速度场，通过求解两组基函数的系数，重构出目标声源单独辐射的粒子速度场。

在数值仿真中，以球形声源和板形声源作为干扰声源，对球形目标声源的辐射粒子速度场进行了重构，结果表明，所提方法均能以较高的精度重构出目标声源的辐射粒子速度场，其中，当干扰声源为球形声源时的重构精度高于当干扰声源为板形声源时的重构精度。在消声室内，使用两个扬声器声源作为目标声源和干扰声源，以较好的精度重构出目标扬声器单独辐射的粒子速度场，对所提方法给予了实验验证。该方法为实际复杂声场环境中，目标声源的辐射粒子速度场的重构提供了解决方案。