平面磨削表面的特征解耦与形貌仿真

石爱娟，叶 丹

（安徽文达信息工程学院机械与汽车工程学院，安徽 合肥 231201）

0 引 言

机械加工粗糙表面的微观形貌仿真一直以来都是摩擦学领域研究的基础性课题之一[1]。微观表面形貌的仿真研究对于机械加工表面质量控制与粗糙表面接触仿真研究具有重要意义[2]。

目前对于平面磨削加工方式下微观表面形貌的仿真应用较多的两种方法有数值模拟方法和几何仿真方法[2]。数值模拟方法是通过设定初始粗糙度参数生成高斯或非高斯表面，实现对平面磨削粗糙表面的仿真方法[3]。WU等[4-5]运用傅里叶变换生成高斯或非高斯表面对平面磨削粗糙表面进行了仿真。WANG等[6]在后续研究工作中基于傅里叶变换与JOHNSON转换系统[7]生成非高斯表面对平面磨削粗糙表面进行了仿真。数值模拟方法得到的仿真表面基于粗糙度表征参数，在统计学角度能够满足相关特征。但后续研究发现[2-3,8]，高斯或非高斯仿真表面无法准确地表征平面磨削表面形貌，甚至会对平面磨削表面有限元接触仿真分析引入误差[9-10]。

几何仿真方法是结合磨削加工参数与砂轮磨粒在磨削过程中的运动轨迹，实现对平面磨削表面的三维形貌仿真方法。WARNECKE等[11]运用切削运动学得到了平面磨削加工过程中砂轮磨粒的运动轨迹方程。NGUYEN等[12-13]基于WARNECKE提出的理论开发了平面磨削表面形貌的仿真模拟程序。CAO等[14]基于NGUYEN等人的理论，在磨削工件表面形貌仿真过程中考虑了砂轮与工件之间的相互振动对表面形貌的影响。CHEN等[15]将表面波纹度信息引入到平面磨削表面的仿真过程中。几何仿真方法能够得到平面磨削加工过程加工参数对表面形貌形成的对应规律。但是，磨削加工过程中存在大量的影响因素，随着研究的进一步深入，几何仿真方法的可行性将大大降低。

本文运用小波分析对于复杂信号多尺度分解的特点，对实测平面磨削表面形貌的采集信号进行分解处理。结合对每层信号分量的小波能量分析以及平面磨削加工过程中的影响因素分析，将复杂的表面形貌信号按照频率信息划分为高频频段、理论频段及低频频段3个频段，实现对复杂表面形貌信号的解耦。并且将提取得到的高频频段与低频频段信息分别进行重构，形成通用仿真模型。结合磨削运动学得到的平面磨削表面理论形貌，最终生成平面磨削仿真表面。继而得到一种基于少量参数的平面磨削表面形貌仿真方法。

1 平面磨削表面形貌成因分析

机械加工零件的表面形貌信号按照不同频率信息范围可划分为粗糙度、波纹度、几何形状误差以及其他随机因素4个组成部分[2]。文献[2]中对于4部分内容进行了详细概述，这里不再赘述。

按照频率信息的划分，可将平面磨削表面三维形貌成因进行归纳，如图1所示。可以看出，实际平面磨削表面形貌形成过程中存在大量的影响因素，倘若通过探索各个影响因素的影响规律对表面形貌仿真进行正向分析，则需针对每个影响因素的信号成分进行单独分析。正向分析方法可行性较差，并且难以做到将全部参数考虑在内，容易造成考虑参数缺失，进而导致最终仿真表面不准确。

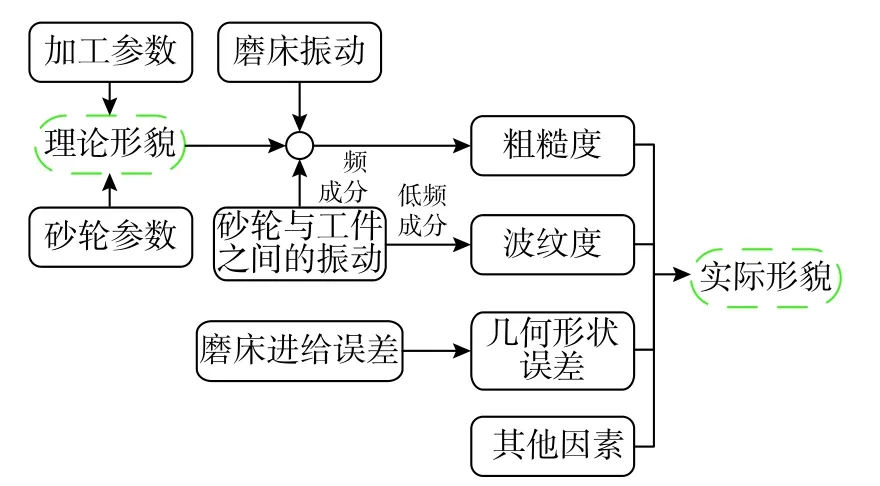
图1 平面磨削表面形貌成因分析

本文从已成型的实际表面形貌着手，基于复杂信号解耦的思想，采用小波变换将实际平面磨削表面形貌信号进行多尺度分解，如图2所示。考虑到理想磨削过程实际上是砂轮对试样表面材料的去除过程，在只考虑砂轮与工件相对运动并且材料能够完全去除的理想条件下，工件获得的平面磨削表面形貌，称为理论形貌。从数据信号角度来讲，理论形貌信号对应一个频段，为理论频段。通过对理论频段的信号进行截取，可实现平面磨削表面的整体信号的三部分划分。

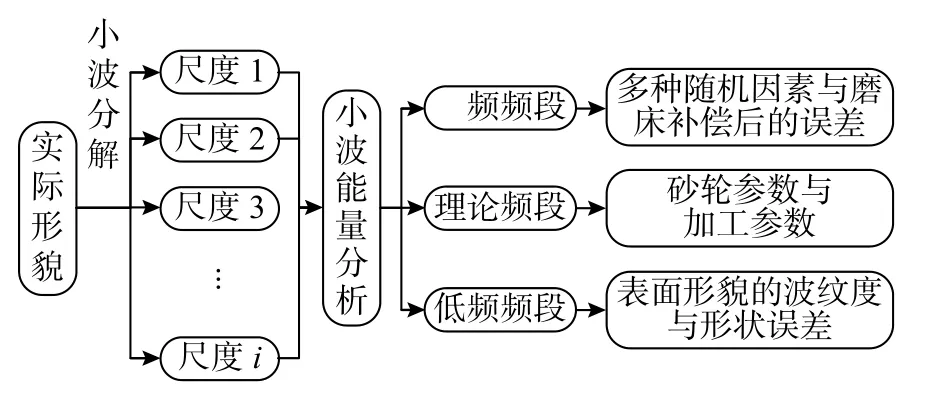
图2 表面形貌信号的小波分解

对于每一频段临界点的划分，需要结合对复杂信号每一尺度下重构信号的小波能量分析，继而可将复杂的形貌信号划分为高频频段、理论频段和低频频段3个频段。高频频段信息中包含多种随机因素与磨床补偿后的误差。低频频段信息中包含实际形貌中波纹度与形状误差等要素。

相比单独对多参量复杂信号正向分析来讲，本方法仅需针对实际形貌信号3个频段进行分析，降低了对于复杂信号分析的难度。并且从另一角度来讲，本文方法可以很好地解决在复杂信号解耦过程中参数考虑缺失与复杂信号无法直接解耦的难题。

2 平面磨削表面形貌的解耦

2.1 平面磨削表面实际形貌的采集

为验证本文方法的可行性，本节将对常见低碳钢Q235的平面磨削表面进行研究分析。采用M1420型万能磨床对试样表面进行磨削处理。选用常见半径 rs=300 mm的单晶刚玉砂轮对试件进行加工，砂轮粒度为60#。并且为保证后期理论磨削形貌的生成，记录试样的加工参数，包括：砂轮转速 n=1 500 r/min，工件的进给速度为vw=10 m/s，磨削进给量ap=10 μm。

采用BMT EXPERT型3D表面形貌分析仪对平面磨削试样表面形貌进行测量。图3所示为粗糙度Sa 0.415 μm下平面磨削表面的采集结果。采样区域为 （3×3） mm2，采样点数为 1 024×1 024。

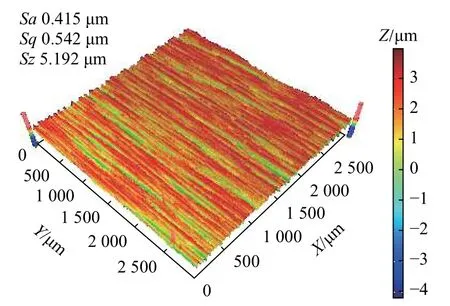
图3 Sa 0.415 μm下平面磨削表面形貌

下节将运用小波变换对复杂的表面形貌数据进行多层分解处理，以实现复杂形貌信号的解耦。

2.2 平面磨削表面形貌的小波分解

小波变换以其多尺度分解的优势，广泛应用于信号处理领域，小波能量分析则是复杂信号解耦较为常用的方法之一[16]。本文将这种小波分析方法引入到复杂表面形貌信号的解耦分析领域。对复杂的平面磨削表面形貌信号进行小波分层处理，并对每个分解尺度下低频重构信号进行小波能量分析。

按照小波分解的思想，将Sa 0.415 μm下平面磨削表面形貌信号进行小波9层分解。分解得到的每层的高频重构形貌如图4所示。表1所示为不同分解尺度下低频重构形貌的小波能量及其占比。

图4 不同分解尺度下高频重构形貌

从表1可以看出，在尺度3到4以及尺度7到8两处，小波能量存在明显的阶跃点，即在阶跃点处小波能量降低幅度较大。基于这两处阶跃点，可以将实测表面形貌信号划分高频频段、理论频段及低频频段。尺度1、2、3下的高频仿真形貌展示了实际形貌信号中的高频成分信息，即多种随机因素与磨床补偿后的误差成分。尺度8、9下的低频仿真形貌展示了实际形貌信号中的低频成分信息，即波纹度与形状误差成分。

表1 不同分解尺度下低频重构形貌的小波能量及其占比

因此，本节把尺度1、2、3下的仿真形貌信号叠加成为高频频段形貌，把尺度8、9仿真形貌信号叠加成为低频频段形貌。图5与图6分比为实际形貌中分离得到的高频频段与低频频段仿真形貌。并且，本文将上述提取整合的高频频段、低频频段仿真形貌作为通用仿真模型，应用于不用加工参数下平面磨削表面形貌的仿真。

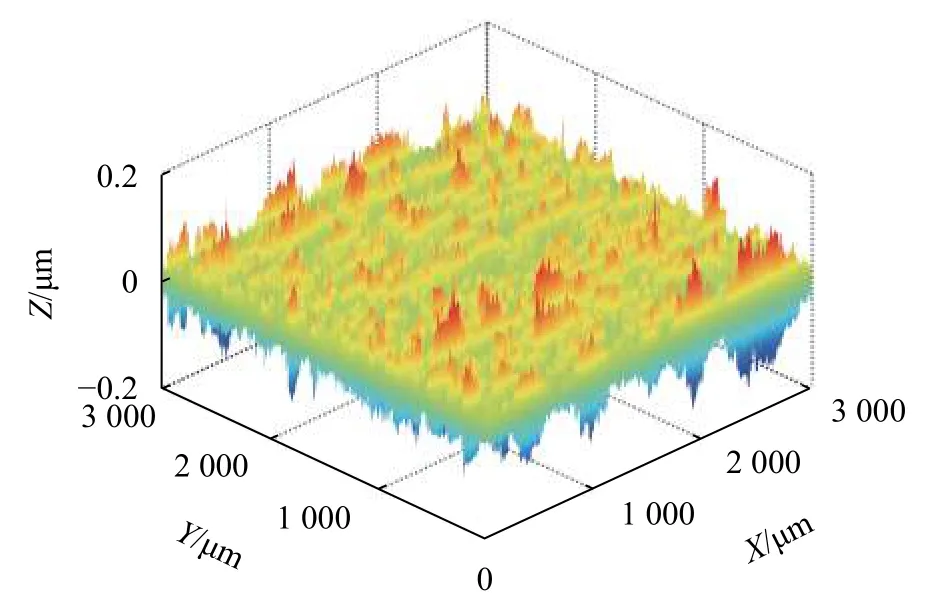
图5 高频频段重构形貌

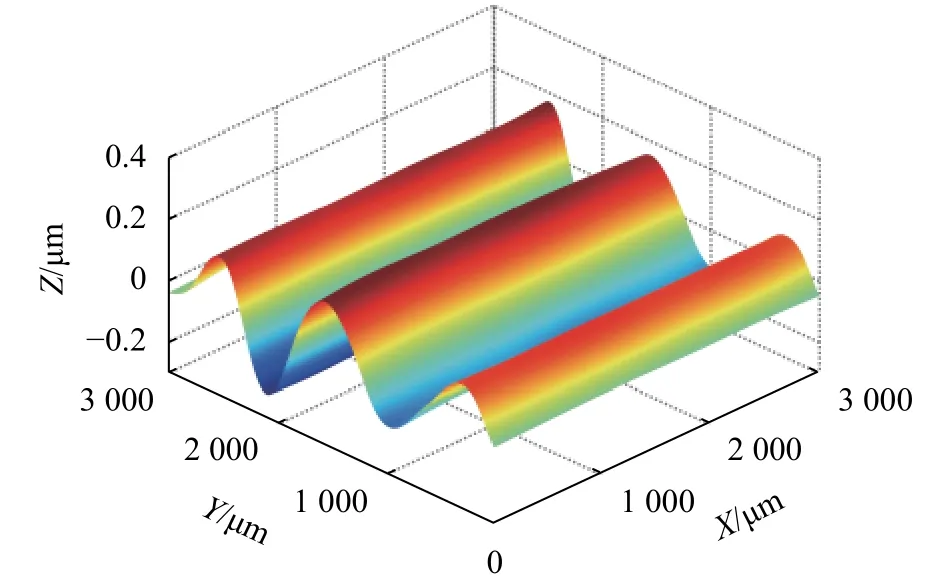
图6 低频频段重构形貌

2.3 平面磨削表面理论形貌的仿真

通过2.2节分析，本文基于实测平面磨削表面提取并重构出通用仿真模型。仿真流程图如图7所示。若想得到完整的平面磨削表面形貌，还需添加理论频段仿真形貌。而理论频段是与砂轮参数及加工参数有关。因此，本节将基于磨削运动学理论，结合砂轮参数及加工参数，实现平面磨削表面理论形貌的仿真。继而结合2.2节得到的高、低频通用仿真模型，最终对实现平面磨削表面形貌的仿真。

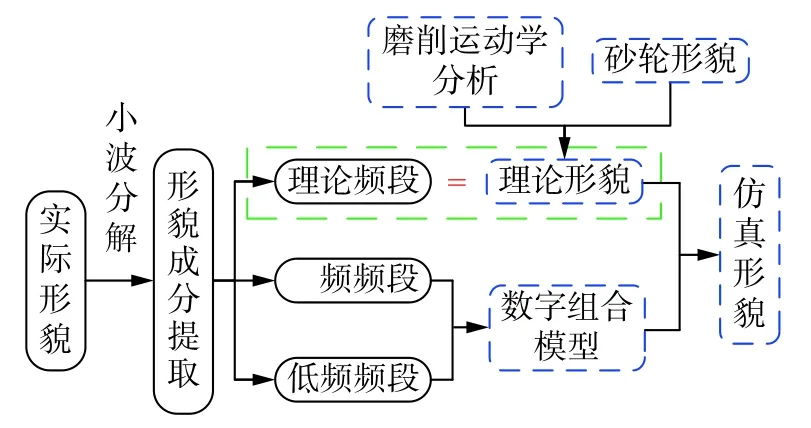
图7 仿真流程图

平面磨削表面理论形貌的仿真需要从磨削用砂轮的表面形貌进行着手。首先，需要对砂轮表面形貌进行仿真；继而，结合磨削运动学理论，即可实现对平面磨削表面理论形貌的仿真。

采用BMT EXPERT型3D表面形貌分析仪对60#粒度下砂轮表面进行三维形貌测量。图8为砂轮表面形貌，测试区域为3 mm×3 mm。

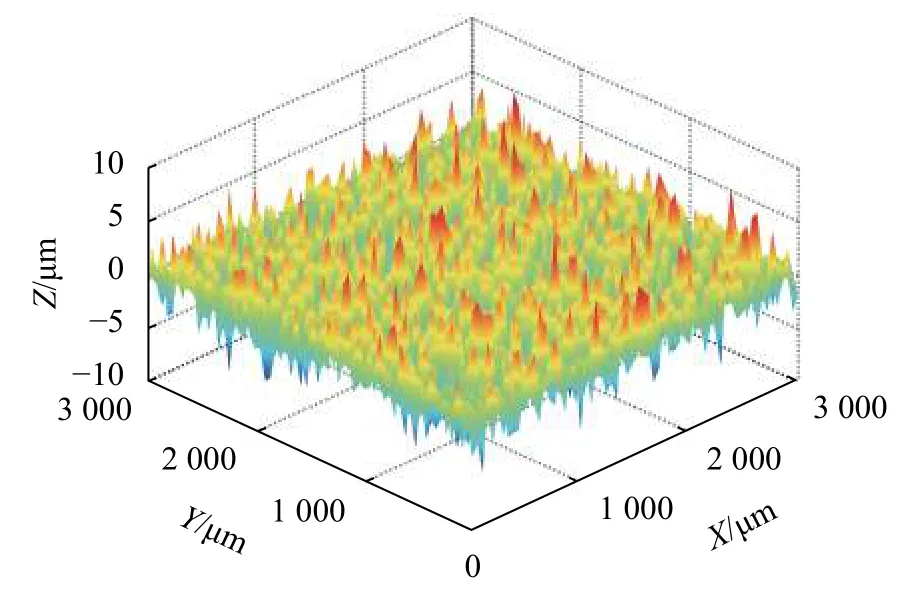
图8 砂轮表面形貌

文献[17]中对于砂轮形貌的仿真流程及实现方法进行了详细说明，这里不再赘述。结合2.1节平面磨削的加工参数，本文按文献[17]所述方法编制相应程序，即可实现对平面磨削表面理论形貌的仿真。平面磨削表面理论形貌仿真结果如图9所示。

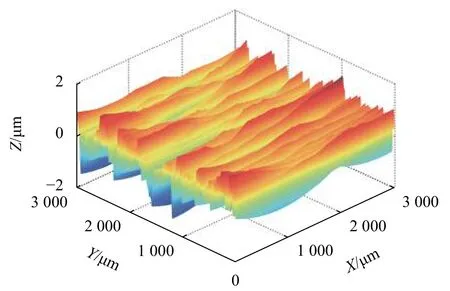
图9 平面磨削表面理论形貌

3 平面磨削表面形貌仿真与误差分析

通过第2节的分析，分别得到了基于实测平面磨削表面形貌的通用仿真模型及平面磨削表面的理论形貌。叠加两者可以得到平面磨削表面仿真形貌。平面磨削仿真形貌如图10所示。

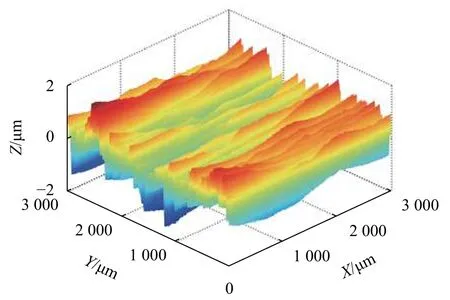
图10 仿真表面形貌

为验证本文提出方法的准确性，选取算术平均偏差Sa、均方根偏差Sq、偏态Ssk、峰态Sku 共4个粗糙度参数对实际形貌与仿真形貌进行对比分析。通过计算，仿真表面的4个粗糙度参数分别为：Sa=0.411 μm，Sq=0.538 μm，Ssk=-0.189，Sku=2.241。首先，分别对试样表面3个区域进行数据采集，对实际形貌与仿真形貌进行对比分析。其次，针对不同磨削进给量 ap（5，10，15，20 μm），对不同工况条件实测表面与仿真表面的粗糙度参数进行对比分析。

3个实测区域的粗糙度参数以及相对仿真表面的粗糙度参数误差如表2所示。不同工况条件下粗糙度参数误差如表3所示。这里对于实测形貌与仿真形貌粗糙度参数的对比是包含对比区域内粗糙表面整体误差的对比，包括粗糙度、波纹度、几何形状误差以及其他要素累计误差。

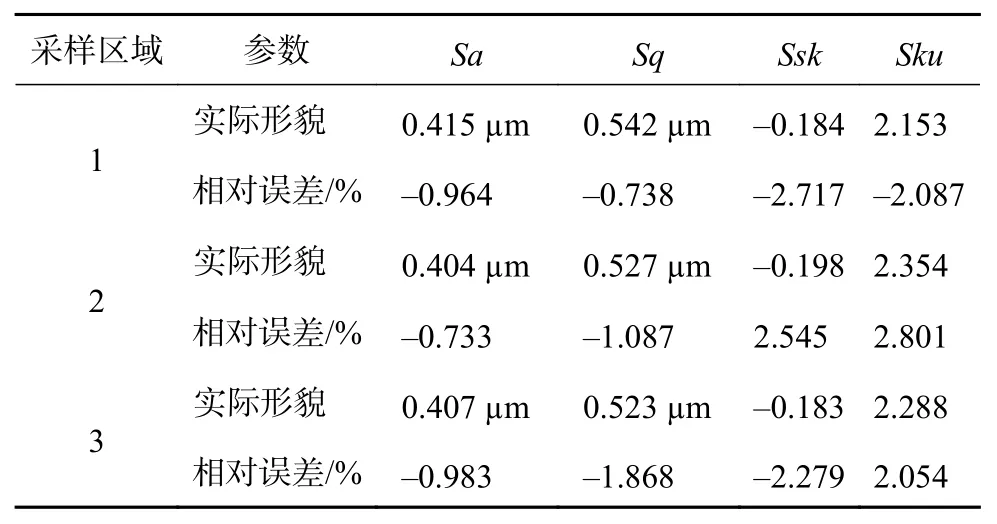
表2 3个区域粗糙度参数计算误差表

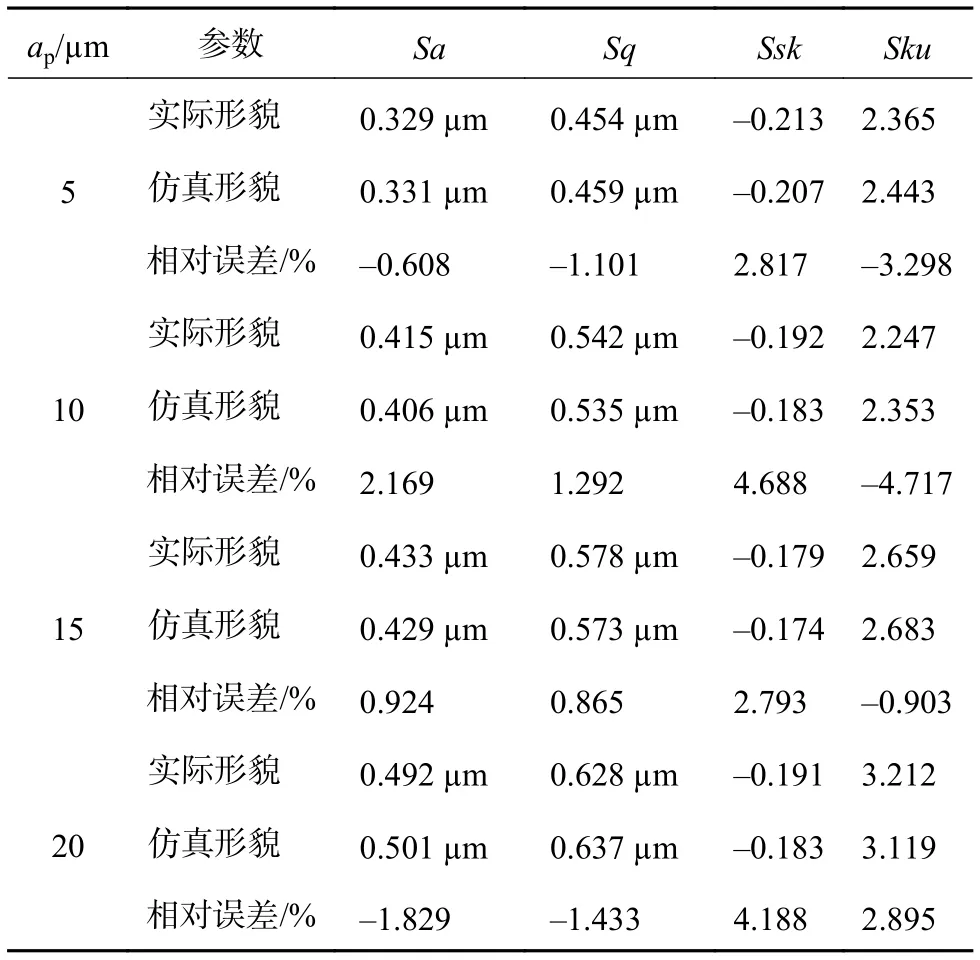
表3 各组试样的粗糙度参数计算误差表

对于3个区域粗糙度参数相对误差，仿真形貌与实际形貌就平均偏差Sa、均方根偏差Sq、偏态Ssk 及峰态Sku 四者的相对误差最大值为2.801%。对于不同磨削进给量 ap下相对误差，平均偏差Sa与均方根偏差Sq来讲，两者相对误差的绝对值较小，误差最大值为2.169%；偏态Ssk及峰态Sku相对误差的绝对值稍大，误差最大值为-4.717%。

从整体对比结果来看，本文方法得到的仿真形貌与实际形貌表面粗糙度参数的相对误差较小，进而验证了本文方法的准确性。

4 结束语

1）本文采用小波分层理论对平面磨削表面形貌信号进行了多尺度分解。结合对分层重构形貌的小波能量分析，将实际形貌按照频率范围划分为低频频段、理论频段和高频频段。将高频频段、低频频段信号叠加形成通用仿真模型。

2）基于磨削运动学原理，得到了平面磨削加工方式下的理论形貌。结合高、低频通用仿真模型与理论形貌，完成了对平面磨削表面形貌的仿真。本文提出的方法为平面磨削表面形貌的仿真提供了一种新的途径。

3）对Q235平面磨削表面的实际形貌与仿真形貌就相关粗糙度参数进行了对比分析。对比结果显示，仿真形貌与实际形貌表面粗糙度参数的相对误差较小，验证了本文方法的准确性。