旋翼减摆自润滑衬套疲劳试验温度设计与控制
马战奇,孙秀文,王玲奇
1.哈尔滨飞机工业集团有限责任公司, 哈尔滨 150066
2.上海市轴承研究所,上海 200031
某型机旋翼为铰接式构型,摆振铰应用自润滑衬套的摩擦阻尼作为减摆阻尼。减摆阻尼是桨毂在旋转平面内的决定性自激振参数,在直升机服役寿命中要求减摆阻尼处于稳定范围内来规避直升机“地面共振”的风险。旋翼在高频摆振运动时,产生大量的热,引起衬套对磨副温度升高。自润滑衬套提供阻尼的材料成分主要为高分子聚合物塑料(聚甲醛POM),该类材料在使用环境温度升高时,其疲劳性能降低、抗蠕变性能降低、稳定性变差[1-6]。因此,自润滑衬套使用温度成为保证减摆阻尼值稳定的关键要素,也是旋翼支柱关键零部件研制中疲劳耐久性考核试验的重要参数。
国内外许多学者对轴承、齿轮及其他摩擦结构的生热、传热、损伤进行了大量研究。李英等提出长时间作周期性旋转或摆动的轴承稳态分析方法[7],闫刚等对聚合物基材料的热导模型及热导率提出了应用建议[8],Khare等通过摩擦试验提出了铜和锡的磨损量与烧结温度关系[9]。Mivehchi和Varvani-Farahani研究了FRP复合材料温度对疲劳损伤累积的影响[10],Laraqi等提出了销盘摩擦装置中的温度和热量分配精确解析解[11],本文从旋翼减摆衬套的疲劳试验考核的角度,开展工程实践应用研究。
直升机在飞行中,旋翼减摆自润滑衬套作持续的、长时间的摆振运动,在摩擦生热及热量分配后,热传导可近似为稳态传热过程[7],热传导涉及不同传热参数的固体传热及高速空气对流换热。自润滑衬套的疲劳考核试验温度主要控制参数为冷却水流入流温度与流速。
通过建立摆振铰摩擦生热、传热模型,分别获得了摩擦副在稳态运转时和试验状态下的理论温度分布,进而为自润滑衬套疲劳耐久性考核试验提供满足要求的控制参数。
1 旋翼运转传热模拟
直升机旋翼运转时,在旋翼离心力作用下,旋翼自激周期摆振运动使得前后支臂在摆振铰处摩擦生热,向两端传递散热,如图1所示。忽略直升机起停车过程,旋翼支臂传热可看作是一个准稳态过程。分析过程分为两步:① 摩擦生热量及热流量分配计算;② 热传导过程温度场计算。
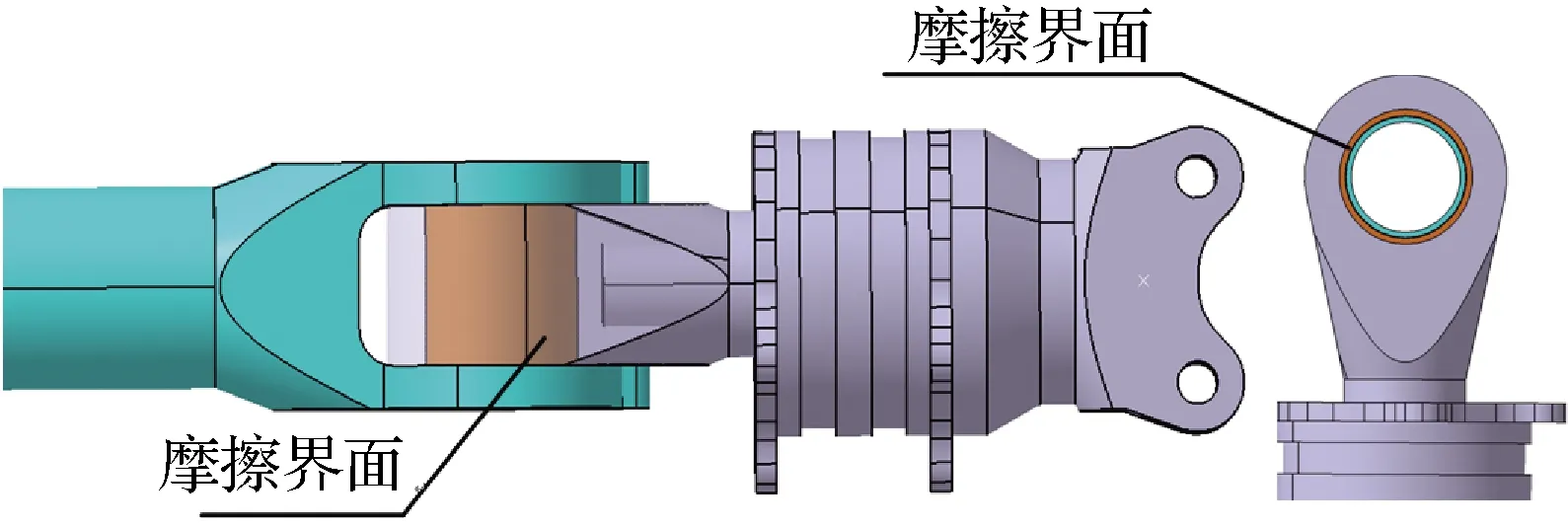
图1 生热模型示意图
假设旋翼周期摆振运动中,认为动能全部转化为摩擦热而被摩擦副吸收,在计算时衬套之间产生的热作为边界热流输入来处理,则摩擦表面输入热流密度满足:
q(θ,t)=fr·p(θ,t)·v(t)=
fr·p(θ,t)·ω(t)·r
(1)
式中:fr为动摩擦系数;p(θ,t)为摩擦表面上的比压,N/m2;θ为零件的相对角位移;t为时间;v(t)为零件的相对位移速度,m/s;ω(t)为角速度;r为径向坐标。
旋翼摆振铰处的离心力在一个相对的时间内数值并不随时间变化,在桨榖摆振周期运动过程中,衬套表面由于摩擦产生的热流量只随着圆周角θ变化。此时热流量可表示为
q(θ)=fr·p(θ)·v=fr·p(θ)·ω·r
(2)
衬套的摩擦接触面挤压力是旋翼离心力在摆振铰处的分布作用,沿圆周分布,如图2所示。图中:R为半径;δ为最大变形;F为径向载荷;L为衬套高度;ΔL为角位移θ处的变形。
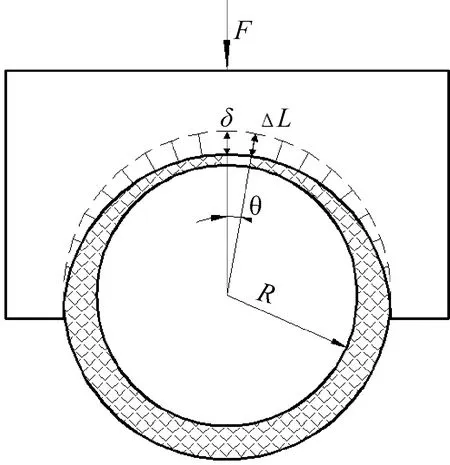
图2 摩擦界面挤压力计算示意图
自润滑衬套工作时所受的应力分布为
(3)
旋翼摆振运动产生自润滑衬套与钛合金衬套之间的相对滑动,与旋翼摆振角度有关。旋翼基频下(1 Ω)的摆振角度谱如表1所示,表中γ为减摆器角位移。

表1 自润滑衬套摆动角度谱
自润滑衬套与钛合金衬套在大部分摩擦运动时间(99.9%时间比例)的相对角位移在γ=±2°以内。按角位移为γ=4°计算角速度ω:
f=272/60=4.53 Hz
式中:f为频率。
旋翼摆振铰由钢基体、均聚甲醛耐磨材料层的自润滑衬套和钛合金衬套构成,摆振铰材料如表2所示。摩擦面为聚甲醛外表面和钛合金内表面,如图3所示。聚甲醛衬垫和钛合金衬套摩擦系数为0.22[8]。得摩擦表面总热流分布为

图3 摩擦界面示意图
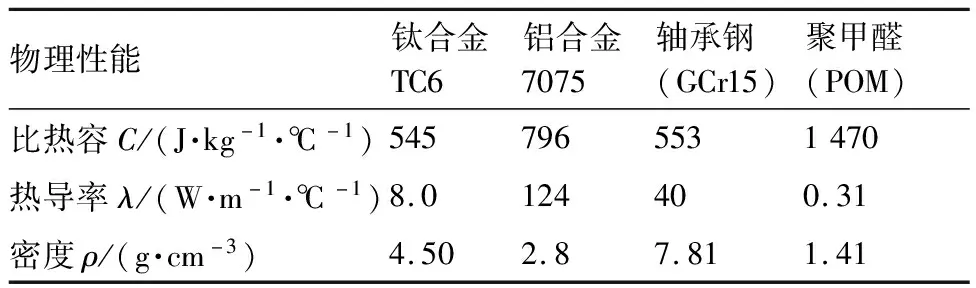
表2 支臂材料物理性能


图4 衬套表面热流量分布
1.1 热流量分配
对自润滑衬套摩擦生热分析实际是一个热与结构耦合的过程[12-16],摩擦热分析中,定量分析摩擦界面的热阻非常困难,应用试验Blok公式[16]进行计算,假定与摩擦表面的热阻无关,并且接触表面的最高温度相等且热流连续。边界条件可表述为,在接触面积内分属2个摩擦体最高温度的接触点配对温度相等。即
(5)
式中:Tpmax为自润滑衬套的最高温度;Ttmax为钛合金衬套的最高温度;η为热流分配系数;qp为分配至自润滑衬套上的热流;qt为分配至钛合金衬套上的热流。
热扩散系数:
式中:下标“t”表示钛合金衬套。
贝克来(Péclet)数:
对于静止的自润滑摆振衬套[12]:
式中:下标“p”表示钛合金衬套。
对于运动的钛合金衬套[12]:
最后可得
计算得热流分配系数为
η=0.374 8
因此,作用在自润滑衬套和钛合金衬套的热流量为
沿摩擦面圆周热流量分布如图5所示。

图5 自润滑和钛合金衬套表面热流分布
1.2 热传递过程
在直升机飞行时,旋翼支臂对流换热问题可以近似地看作为一个流体(空气)横向绕流单个圆柱体的强制对流稳态换热问题。圆柱表面的换热系数主要与表面流体的速度有关,而圆柱表面的流体速度由于边界层和尾涡的形成,沿圆周一圈变化,换热系数也随之变化。在工程实践中平均换热系数有重要意义。
绕流圆柱体的努塞尔(Nusselt)数为
式中:α为换热系数;d为圆柱直径;Cc、n和m取值依据表3条件确定。

表3 流体绕流单个圆柱的常数取值
旋翼支臂质心处平均线速度为
v=ωR=16.24 m/s
设定旋翼使用环境温度上限为40 ℃,此时空气的物理性质见表4。

表4 空气的物理参数
模型尺寸如图6所示。对于图6中实线合围区域换热系数α1的计算,支臂前段雷诺数为
空气的普朗特数:
Pr=0.699
取Cc=0.26,n=0.6,m=0.38,有
可得α1=64.88 W/(m2·℃)。
对于图6中虚线合围区域换热系数α2的计算:

图6 旋翼支臂尺寸
α2=50.24 W/(m2·℃)
平均换热系数:
参考文献[17-19]中的方法,建立了直升机旋翼支臂平均意义运转状态热传导细节有限元模型,如图7所示。热源为qt(θ),换热边界条件为空气强制对流,换热系数为57.367 W/(m2·℃)。
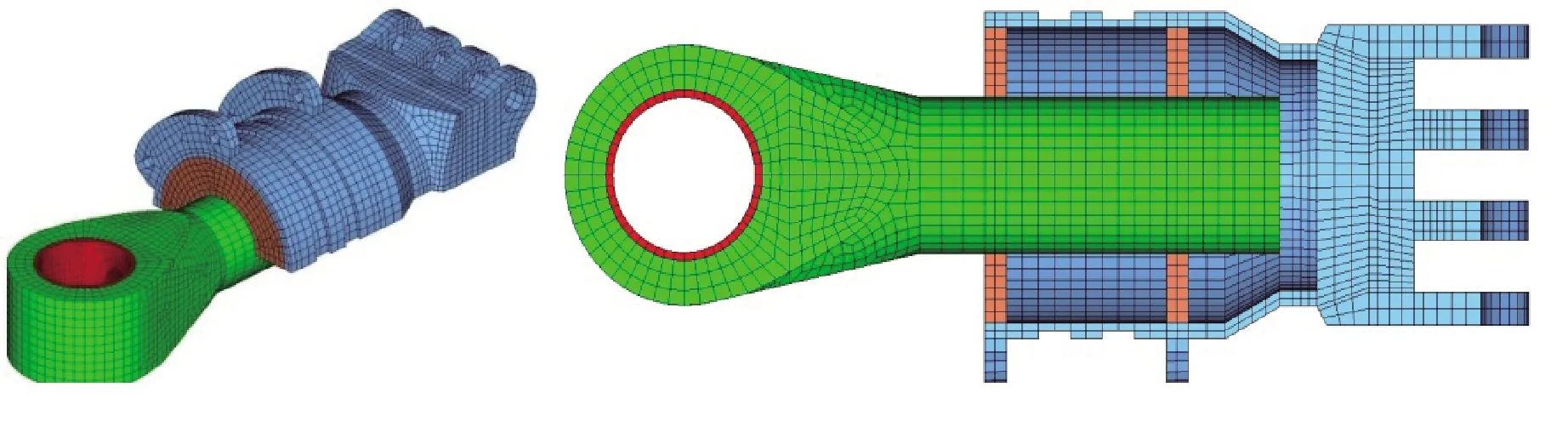
图7 有限元模型
将旋翼支臂内腔油脂温度作为旋翼支臂计算模型中的内腔边界条件。计算的温度分布如图8~图10所示。分析结果显示,钛合金衬套最高温度为65 ℃。根据摩擦界面等温假设,自润滑衬套外表面温度等于钛合金衬套温度。

图8 总体温度分布结果

图9 钛合金衬套温度分布结果
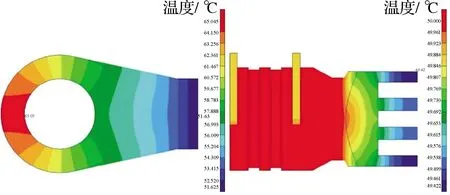
图10 支臂前段和后段温度分布结果
2 疲劳试验夹具传热分析
自润滑衬套疲劳耐久性考核试验工作环境温度应能保证服役寿命期内摩擦阻尼稳定,在施加旋翼离心力与摆振角的情况下要求试验装置(见图11)的散热效率不高于旋翼支臂实际散热效率。

图11 试验装置示意图
试验控温方式为加载块通水冷却,冷却水流的速度、水温为试验装置控制自润滑衬套温度的输入参数。加载块水流管道布置如图12所示。

图12 试验加载片水冷却示意图
2.1 水流换热参数计算
试验夹具水冷过程可以近似看作是一个水流(无变相)管内对流传热问题,按冷却水流速vw=3.54 m/s,特征温度为20 ℃进行试算,冷却水和加载块工装的物性参数[20]如表5所示。

表5 冷却水和加载块的物理参数
由密度ρ=998 kg/m2,动力黏度μ=1.005×10-3Pa·s,得到紊流雷诺数:
流体流态为紊流,流体在圆形光滑管内紊流努塞尔数为
(6)
式中:普朗特数的表达式为
流体被加热,k取0.4,代入式(6),得到对流换热系数为
α=13 017.53 W/(m2·℃)
l/d=260/10<60(l为流管长度),流管为短管,对流换热系数α需采用短管系数fc修正[21],fc的表达式为
当雷诺数处于2 300~105时,紊流流体处于过渡区,换热系数需考虑过渡区修正系数f′c[21],f′c的表达式为
修正后水流换热系数为
α′=α×fc×f′c==14 292.17 W/(m2·℃)
当雷诺数Re<2 300时,水流形态为层流态,此时对流传热系数采用西德尔-泰特关联式计算:
式中:μw为管壁温度下水的动力黏度。
努塞尔数:


不同冷却水入流流速及不同流态的换热关系如图13所示。
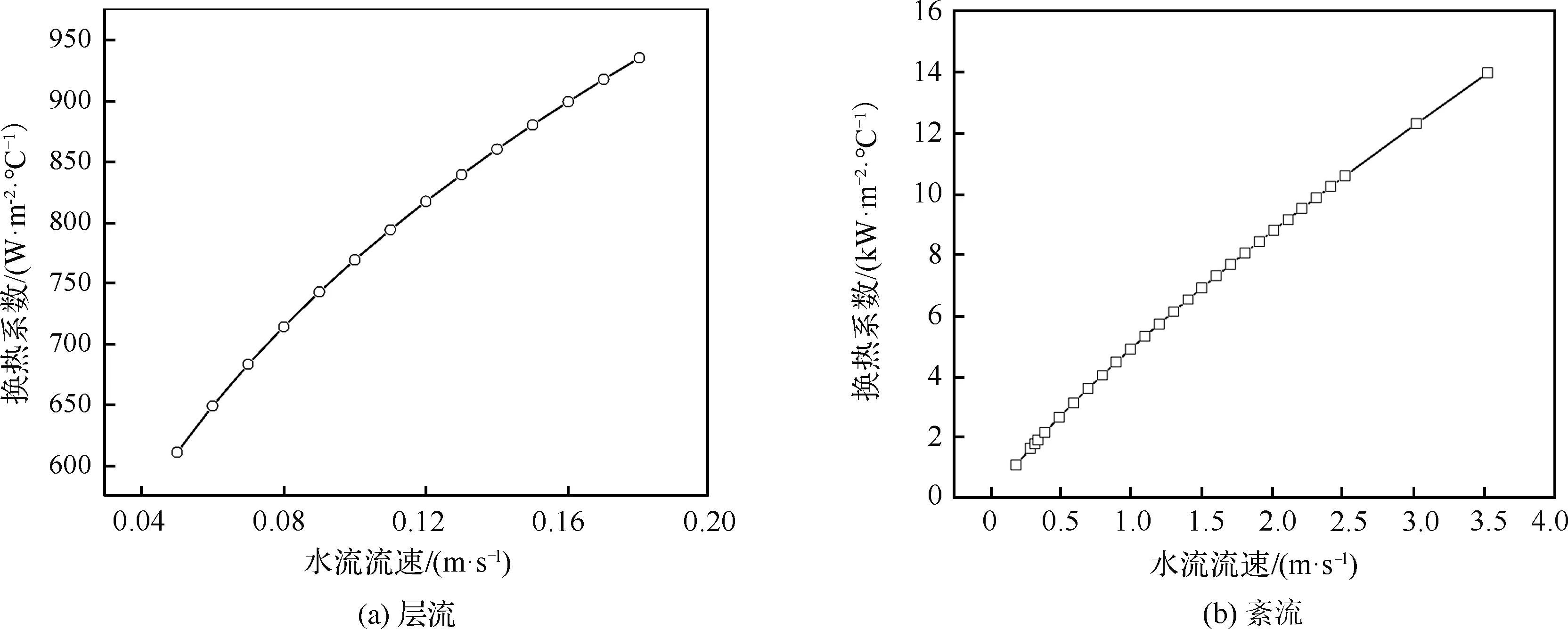
图13 层流、紊流流速与换热系数的关系
2.2 温度分布计算结果
将换热系数α′作为有限元模型换热外边界求解计算,温度云图结果如图14和图15所示。计算结果显示,当冷却水入流温度为20 ℃,入流冷却水流速为3.54 m/s时,试验装置的散热效率较高,试验件最高温度为26 ℃。

图14 加载块温度分布
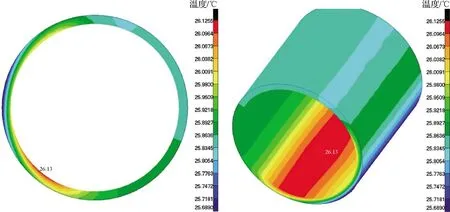
图15 钛合金衬套温度分布
控制不同冷却水入流流速和温度,得到不同换热系数下加载块温度分布如图16所示。计算得到冷却水流换热系数与自润滑衬套最高温度的关系如图17所示。

图16 不同换热系数下的温度分布

图17 不同换热系数及特征温度下的钛合金衬套最高温度
通过计算获得了试验装置冷却水入流参数与自润滑衬套试验中最高温度之间的关系,如入流水温在30 ℃,流速为0.2 m/s时,试验装置的散热效率与飞行时旋翼支臂散热效率相当。
3 结 论
1)自润滑衬套摩擦产生的热量大部分通过钛合金衬套一侧传导,其余通过自润滑衬套一侧传导。热流量沿衬套周向呈余弦分布,在旋翼轴线方向处达到最大值。
2)计算表明,在飞行中旋翼运转时摆振铰自润滑衬套最高温度控制线为65 ℃。
3)获得了试验装置冷却水入流参数与试验时自润滑衬套最高温度之间的关系,实现了试验的合理控温。

