基于优化Teager 能量算子的齿轮箱故障特征频率提取方法

金 宇，龚廷恺，杨 蓓

（南昌航空大学 通航学院，南昌 330063）

0 引言

在众多机械部件中，齿轮箱作为一种典型的传动通用零部件，其在运输机械、电力装备、冶金机械、航空等领域中有着广泛的应用。齿轮一般工作于交变的工况下，随着时间的推移，其失效无法避免，进而影响到整个设备的安全和制造企业的经济效益。及时、有效地诊断出齿轮故障诊断在理论和工程应用中显得尤为重要[1-2]。

在齿轮故障诊断领域，基于振动信号处理的方法已有众多的研究和应用。小波理论通过在不同时间以不同频率的一系列振荡函数来解析信号，可以将原始信号的时频特性更好地表征出来，广泛用于检测轴承故障及齿轮箱故障[3-6]。但是，这种方法具有一定的局限性，包括干扰项、边界失真和能量泄漏等，这些都会产生很多微小的不可预测的尖峰，难以解释和分析所得到的结果[7]。目前，经验模式分解作为一种自适应信号解调方法在故障诊断领域得到了广泛的关注[8-10]，该理论认为复杂信号可分解为一组完整的、几乎单调的本征模态函数，其中某些函数比原始信号包含了更多的故障信息。然而，这种方法都存在着模式混合、敏感于噪声和采样率等问题[11]。

作为一种非线性差分算子，Teager 能量算子能够将信号的瞬态特性显现出来，对被检信号中的冲击分量更为敏感，具有较好的时间分辨率。针对滚动轴承故障诊断问题，王洪明[12]提出了一种基于本征时间尺度分解和矢Teager 能量算子的解调新方法，从构建的仿真信号来看，该方法是有效的，将该方法与Hilbert 包络解调法相比较，从解调结果可知两方法的一致性良好。李浪[13]提出一种基于VMD 与Teager 能量算子的风电机组轴承故障诊断方法，即先使用VMD 处理振动信号并根据峭度指标筛选得到敏感本征模态函数，将敏感本征模态函数经Teager 能量算子和傅里叶变换处理，得到其Teager 能量谱，进而得到故障特征频率。王凤利等[14]考虑到集经验模态分解中的参数选择和轴承故障解调问题，构建了一种基于参数优化集合经验模式分解和Teager 能量算子的复合算法，并应用于滚动轴承的内、外圈失效识别。上述研究发现，Teager 能量算子解调应用中常借用其他方法作为辅助工具，其原因主要是由于强噪声对于分析的干扰了该解调方法的分析结果，进而先通过相应信号方法进行预处理，以便突出原始信号中的故障特征内容，最终实现更好的故障特征解调效果。

在Teager 能量算子处理低信噪比的齿轮故障数据时，提取故障特征频率存在困难。针对该问题，本研究构造了自适应Teager 能量算子算法，并通过仿真信号和实际振动信号的故障识别和诊断证明其有效性。

1 Teager 能量算子理论

一般而言，将信号的幅值平方再积分，所得称为信号能量，它代表的是系统的势能或者动能，是信号幅值的平方的积分，无法表征系统的总能量。当系统产生冲击时，会引起系统的总能量变化。此时，若是通过信号能量来观察冲击特征，会存在一定的困难。因为当冲击特征的幅值较小，噪声能量在信号整体能量中比率较大，从而使得有用信号能量被淹没。

Teager 能量算子的定义是信号幅值的平方和振动频率平方的乘积，其跟踪的是冲击的总能量（包括势能和动能）。相比信号能量，Teager 能量算子额外乘上了频率的平方。另一方面，当齿轮失效时所产生的脉冲信号具有较高的幅值，且频率高。相对信号能量，Teager 能量算子能够更好地抑制噪声能量对于信号整体能量的影响，突出原始振动信号中的冲击特征成分。

将Teager 能量算子记为 ψ，对任意的连续信号x(t)，设定该信号的Teager 能量算子：

另一方面，对于劲度为k的弹簧及质量为m的物块构成的线性无阻尼振动系统，根据牛顿运动定律建立其运动数学模型：

式中：x(t) 是相对于平衡点的位移，是x(t)对时间的二阶微分（加速度），解此二阶微分方程可得：

计算式(3)对时间变量t的一阶与二阶导数，得到物块的速度和加速度：

式中：A为振动幅值，ω=(k/m)1/2为 固有频率，φ为初始相位。无阻尼振动系统在任意的时刻下，其机械能等于物块的动能和弹性势能的和：

将式(3)、式(4)代入式(6)，可得：

由此得出，简谐运动任意时刻的总能量和频率的平方及振动幅值成正比的关系。

将式(4)、式(5)代入Teager 能量算子的式(1)，可得：

将式(7)、式(8)对比可得：两式只相差m/2，即系统的瞬时总能量和Teager 能量算子 ψ仅相差常数m/2。因而系统总能量是能被Teager 能量算子跟随。对于离散信号x(n)，式(1)离散化的差分方程为：

据式(9)可知：对于任意时刻n，仅需3 个采样数据点就可计算离散信号的Teager 能量算子。而且，Teager 能量算子能跟踪系统总能量，所以Teager能量算子 ψ对信号的突变敏感，计算简单，能够很好地显现信号的瞬态分量，对信号进行解调。

2 齿轮故障振动信号分析

2.1 仿真信号分析

在齿轮箱发生故障的时候，周期性的啮合振动信号将会发生调制现象，且在实际情况中齿轮箱振动信号一般会同时发生调频和调幅现象，从而在实际的信号频谱中，中心为固有频率或啮合频率的边频带是调频与调幅同时作用的结果。在仅有调频或调幅作用时，振动信号的频谱图中，边频带一般是关于啮合频率或固有频率对称的。但在调频与调幅同时作用时，这种对称性将会被破坏，因而在观察实际测得的振动信号时，边频带总是不对称的[15]。

依据上述分析，仿真信号数学模型为：

式中参数设定为：信号幅值A=1，调幅调制参数B=1，调频调制参数 β=0.5，载波啮合频率fm=400、特征频率fn=23。

由于本研究针对低信噪比的齿轮箱振动信号，该调幅调频信号添加高斯白噪声，信噪比为−10 dB，形成齿轮箱振动仿真信号，采样点数为4096，信号采样率为2048 Hz。如图1 所示，此为仿真信号的时域图和频域图。通过观察频域图1b可知，频域中载波频率fm和特征频率23 Hz 成分因强噪声干扰而未被提取，因此通过建议方法对其进行处理。

图1 仿真信号时域图频谱图Fig.1 Waveform and frequency spectrum of simulated signals

通过计算发现，该方法在进行到第3 次计算后获得了最大峭度值4.13，即优化过程结束，相应的解调结果如图2 所示。图2a 中能够较清晰地看出原始仿真信号的突变处，同时，图2b 中频谱内容的主要峰值出现在特征频率fn处，该仿真信号分析表明这个优化方法能够有效消除强噪声影响，突出特征信息成分。

图2 仿真信号二次能量算子处理后时域图和频谱图Fig.2 Waveform and frequency spectrum of simulated signals obtained by second-order Teager

2.2 风电机组齿轮箱故障诊断

该风电机组额定功率为3 MW，故障齿轮齿数为32，输出转速1800 r/min，采样时间为2 s，采样率为97 656 Hz，啮合频率fm为960 Hz，故障特征频率为28.3 Hz。齿轮故障振动信号的时域波形（图3a）中存在着明显的噪声成分，造成信号的信噪比较低，其频域图（图3b）中低频范围中没有发现故障特征频率及其谐波成分，同时以啮合频率为中心的两旁也未出现以特征频率为间隔的边频调制现象。因此，使用自适应Teager 能量算子对该信号进行处理，进行二次运算后，信号的峭度值为最大的12.5。其时域图（图4a）中已经可以发现明显的冲击信号，频域图（图4b）中也可以观察到故障特征频率及其谐波，所以该方法对这个风电机组齿轮箱的故障诊断是有效的。

图3 齿轮箱振动信号时域图和频谱图Fig.3 Waveform and frequency spectrum of fault gear signals

图4 齿轮箱振动信号二次能量算子处理后时域图和频谱图Fig.4 Waveform and frequency spectrum of fault gear signals obtained by second-order Teager

为了论证ATEO 算法的合理性，继续对同一故障振动信号分别进行一次和三次计算。图5 为一次Teager 能量算子处理的时域图和频域图，图中仍然存在着大量的噪声，因此其频率图中只有故障特征频率fn被微弱地提取，此时峭度值为5.23。这个结果表明，因噪声干扰，造成一次Teager算子故障解调能力较弱。三次分析后信号的峭度值为6.56，时域波形和频域波形见图6，尽管图中可以观察到齿轮故障特征，但二次分析结果相比较，该结果的故障特征提取效果明显减弱。上述对比结果表明：根据Teager 能量算子的差分方程式(9)，对于离散信号而言，在计算第n个采样点的Teager 能量算子时，只需使用n−1、n、n+1共3 个采样点。当所计算的第n个采样点为齿轮箱故障冲击的峰值点时（即此时处于故障冲击），齿轮箱振动水平大，x(n)与x(n−1)、x(n+1)之间的差值较大，[x(n)]2的 值与x(n−1)·x(n+1)的值差距会较大，具有解调冲击特征的作用。当所计算的第n个采样点为齿轮箱啮合振动信号的点时或为噪声信号时（即此时无故障冲击），齿轮箱振动强度较弱，x(n)与x(n−1) 的差值及与x(n+1)的差值较小，因此，[x(n)]2的值与x(n−1)·x(n+1)的值较为接近，计算得到的Teager 能量算子 ψ[x(n)]的值较小。通过这种自适应方式，经过多次计算逐步减少噪声干扰问题，并通过峭度参数作为计算次数的选取依据，最终实现故障特征的有效识别。

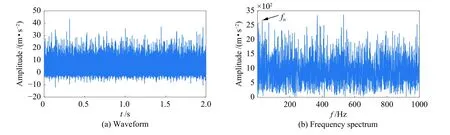
图5 齿轮箱振动信号一次能量算子处理后时域图和频谱图Fig.5 Waveform and frequency spectrum of fault gear signals obtained by first-order Teager

图6 齿轮箱振动信号三次能量算子处理后时域图和频谱图Fig.6 Waveform and frequency spectrum of fault gear signals obtained by third-order Teager

3 结论

1）针对齿轮箱故障状态下低信噪比信号的故障识别问题，提出自适应Teager 能量算子方法，即通过多次Teager 算子计算来降低噪声对于故障解调的影响。

2）对仿真信号和风电机组齿轮箱的故障振动信号进行分析后发现，处理后的信号峭度值约提升了1 倍，进一步改善了齿轮微弱故障诊断精度。