R软件在数值计算中的应用——以圆周率的近似计算为例

李洪毅，贺 陵，周盛康

(吉首大学数学与统计学院，湖南 吉首 416000)

当前，在工程、系统科学、高新技术等诸多领域的数值计算都离不开统计软件，常用的统计软件有R、Matlab、SAS等。R软件是一个开源、免费的统计软件，具有强大的统计分析和数值计算功能[1-3]。以圆周率的近似计算为例，详细介绍了R软件在数值计算中的广泛应用。

1 基于Buffon投针实验计算圆周率

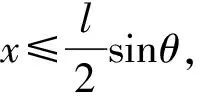
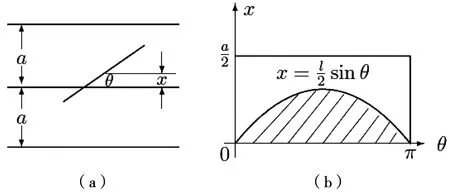
图1 Buffon投针实验的几何概型

基于R软件在计算机上实现Buffon投针实验并近似计算圆周率π的步骤为：

第一，产生随机数。首先产生n个相互独立的随机变量θ，x的抽样序列θi，xi，i=1，2，…，n，其中θi～U(0,θ),xi～U(0,a/2)。

基于R软件将上述步骤编写模拟程序Buffon.r如下：

Buffon<-function(n, l=0.8, a=1){

k<-0; i<-1; pai=rep(0,n); set.seed(666)

while(i<=n){

theta_i<-runif(1, 0, pi); x_i<-runif(1, 0, a/2)

if(x_i<=l/2*sin(theta_i))

k<-k+1

pai[i]=2*l*i/(k*a); i=i+1}

return(pai)}

图2 圆周率π的估计值随实验次数n(≤10 000)变化的动态图

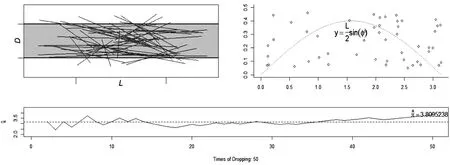
图3 基于buffon.needle函数Buffon投针实验的动态模拟结果(n=50)

2 基于概率分析法计算圆周率

图4 基于概率分析计算圆周率的几何概型

基于上述结果计算圆周率π的近似值，具体步骤为：

第一，产生随机数。首先产生n个相互独立的随机变量X与Y，X与Y的抽样序列xi，yi，i=1, 2,...,n，其中xi～U(0,1),yi～U(0,1)。

基于R软件将上述步骤编写模拟程序PA.r如下：

PA<-function(n){

k<-0; i<-1; pai=rep(0,n); set.seed(666)

while(i<=n){

x_i<-runif(1);y_i<-runif(1)

if(x_i^2+y_i^2<1)

k<-k+1

pai[i]=4*k/i; i=i+1}

return(pai)}

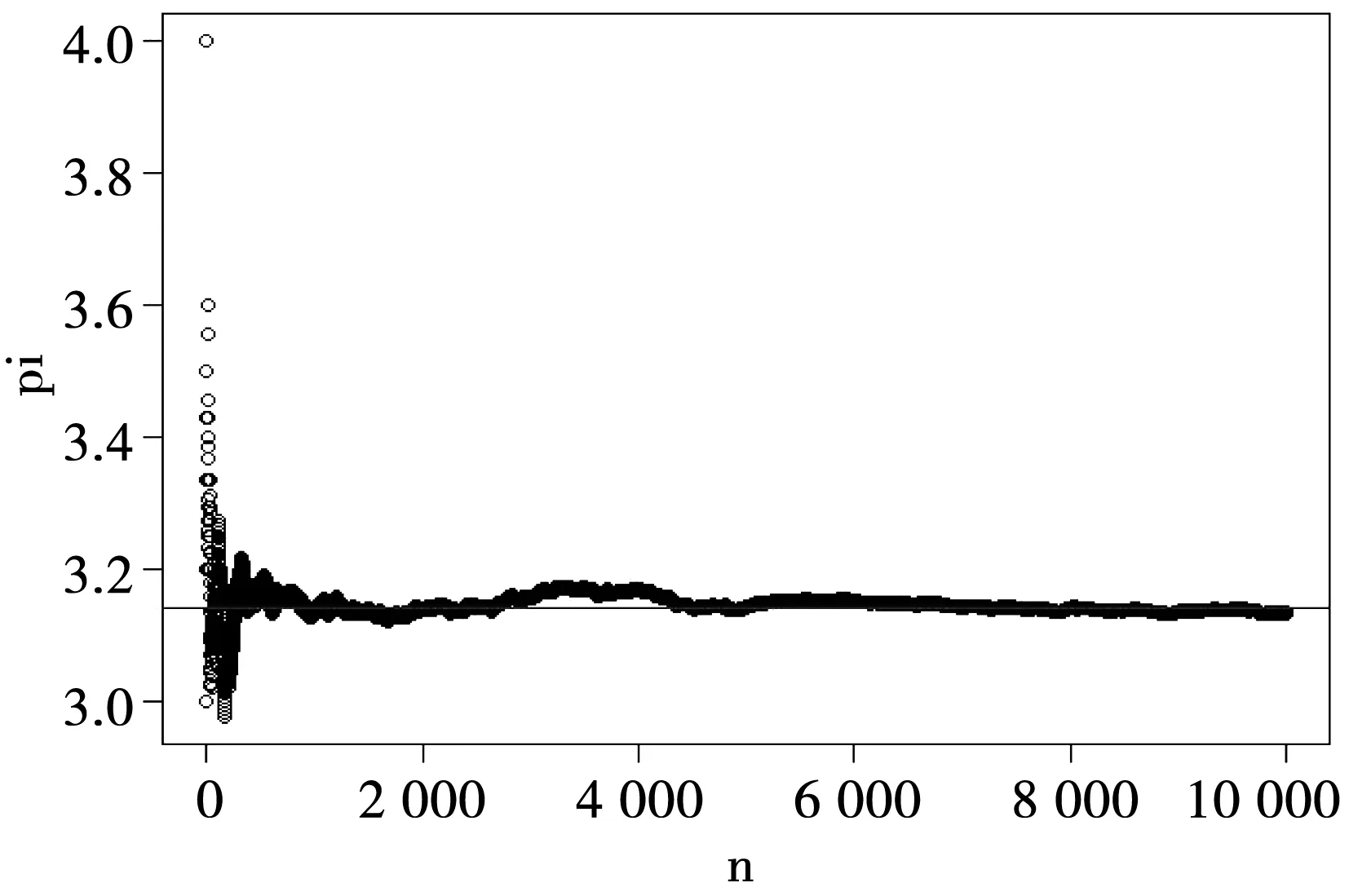
图5 圆周率π的估计值随实验次数n(≤10 000)变化的动态图

3 基于Monte Carlo方法计算圆周率

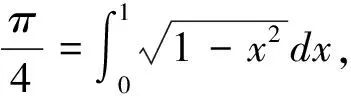
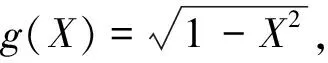
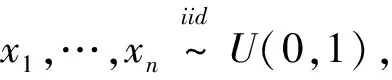
基于上述结果计算圆周率π的近似值，具体步骤为：

第一，产生随机数。首先产生n个相互独立的随机变量X，X的抽样序列xi，i=1,2,…,n，其中xi～U(0,1)。

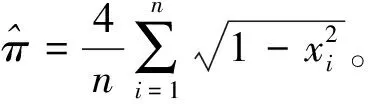
基于R软件将上述步骤编写模拟程序MC.r如下：

MC <-function(n){

i <-1; pai=rep(0,n); set.seed(66)

x <-runif(n)

for(i in 1:n)

pai[i]=4*sum(sqrt(1-x[1:i]^2))/i

return(pai)}

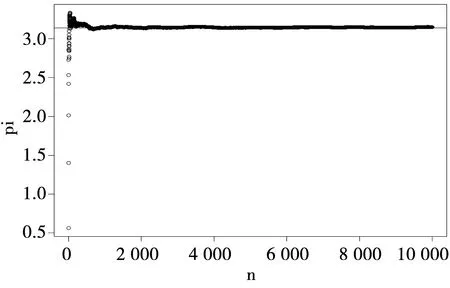
图6 圆周率π的估计值随实验次数n(≤10 000)变化的动态图

4 结语

以圆周率的近似计算为例，详细介绍了R软件在数值计算和数值模拟中的具体应用，由文中实例可以发现：R软件能够非常高效、便捷地解决数值计算和数值模拟中的近似计算问题。教学实践和研究实践证明，R软件可以为统计学、数学专业课程教学和科学研究提供有力支撑，一方面可以加深学生对基本概念和算法的理解，更好地掌握数学理论方法，另一方面还可以通过R软件优秀的图形功能加强计算结果的展示，使学生加深对数学理论方法的理解，更好地处理实际问题，激发学生学习兴趣和动力，为学生更好地应用专业知识处理实际问题奠定坚实基础，对其今后的工作和学习产生积极作用。