钢管混凝土构件的介质多相性及导波检测

刘鹏飞, 刘南希, 李祚华, 于洪涛, 滕 军, 陈 杰

(1.深圳市建筑设计研究总院有限公司，深圳 518031；2.哈尔滨工业大学(深圳) 土木与环境工程学院，深圳 518055)

钢管混凝土利用钢管和混凝土两种材料在受力过程中相互间的组合作用，充分发挥两种材料的优点,一方面能改善混凝土的塑性和韧性，另一方面可避免或延缓钢管发生局部屈曲，使钢管混凝土具有承载力高、塑性和韧性好、经济效果好和施工方便等优点[1]。钢管混凝土构件一般作为柱子等关键受力构件，一旦失效将会降低建筑结构整体的安全性，造成损失[2]。因此，为了及时发现潜在的安全隐患，避免事故发生，对这种关键受力构件进行定期的检测是十分重要的。基于导波的检测方法成本较低、操作简单、效率高、具有针对性又可满足全面性，受到了广泛关注[3-4]。

为了研究在不产生明显频散的激励频率下，钢管混凝土介质多相性及轴向缺陷产生的导波回波信号的变化，笔者基于有限元软件ABAQUS，分别创建钢管砂浆骨料分层模型、基于Monte Carlo方法(一种统计模拟方法)的随机圆形骨料模型和钢管混凝土构件含轴向缺陷的模型，模拟导波在钢管混凝土中的传播情况，以此来分析导波回波信号的变化。

1 介质多相性引起的导波回波信号变化

钢管混凝土构件中，混凝土骨料的粒径是随机分布的，试验条件很难直接控制这一变量，但试验结果却会受到这种随机分布的影响。基于伍君勇[5]对混凝土结构细观模型进行的研究，笔者将混凝土看作一种复合材料，其由砂浆和骨料组成，具有多相性。由此，创建钢管混凝土构件的有限元分析模型。

1.1 骨料层密度对导波传播的影响

选用solid单元(一种有限元单元类型)，外层为钢材，内层为混凝土材料，两者间以tie(一种接触方式)连接，模型全程处于弹性阶段。钢管混凝土模型长为3 200 mm，直径为100 mm，壁厚为5 mm。

混凝土构件中骨料和缺陷的存在都会使导波的传播路径发生变化，引起导波散射和能量耗散。为研究骨料层密度的变化导致的导波回波信号的变化，在砂浆中按不同密度布置骨料层来进行模拟。单一骨料层和骨料层整体分布如图1所示。以构件轴线与截面的交点为圆心，在直径为90 mm的范围内进行导波激励，激励频率为10 kHz，导波信号为汉宁窗调制信号，提取到的响应信号如图2所示。

图1 单一骨科层和骨科层整体分布示意

图2 不同骨料层的导波回波信号

由图2可知，对于整体信号而言，骨料层的密度变化导致的信号变化非常小。为研究不同骨料层密度的影响，放大信号的平稳段，得到如图3所示的信号。

图3 不同骨料层的导波回波信号(放大后)

由图3可知，随着骨料层密度增大，骨料反射回波幅值逐渐增大，提取信号中包含的骨料信息也增多。即便如此，相对于发射信号和回波信号的幅值骨料反射回波幅值极小。

1.2 骨料含量对导波传播的影响

为研究骨料含量的变化导致的导波回波信号的变化，在ABAQUS软件中创建混凝土构件的二维模型，通过改变骨料面积占比来模拟骨料的含量。

基于Monte Carlo方法，以骨料面积占比为指标，假定混凝土构件中骨料的分布和粒径均为随机的[6]，生成骨料面积占比分别为0%，20%，25%，30%，35%，40%，45%和50%的混凝土构件模型，在ABAQUS软件中导入这些模型，创建随机圆形骨料模型。图4为骨料面积占比分别为0%，30%，40%和50%的混凝土构件模型，图5为模型加载的示意图。

图4 不同骨料面积占比的模型

图5 模型加载示意

在不同骨料面积占比的随机圆形骨料模型的顶部提取响应信号进行分析。以骨料面积占比为30%的模型为例模拟导波传播的过程，其在各时刻的响应云图如图6所示。

从图6可以看出，初始状态下试件整体处于零响应状态。导波信号从试件的顶端出发，随着时间增长，导波沿试件轴向传播，并与试件边界和内部骨料相互作用，内部响应情况逐渐复杂。导波到达试件底端后，开始反向传播，并最终返回到试件顶端。

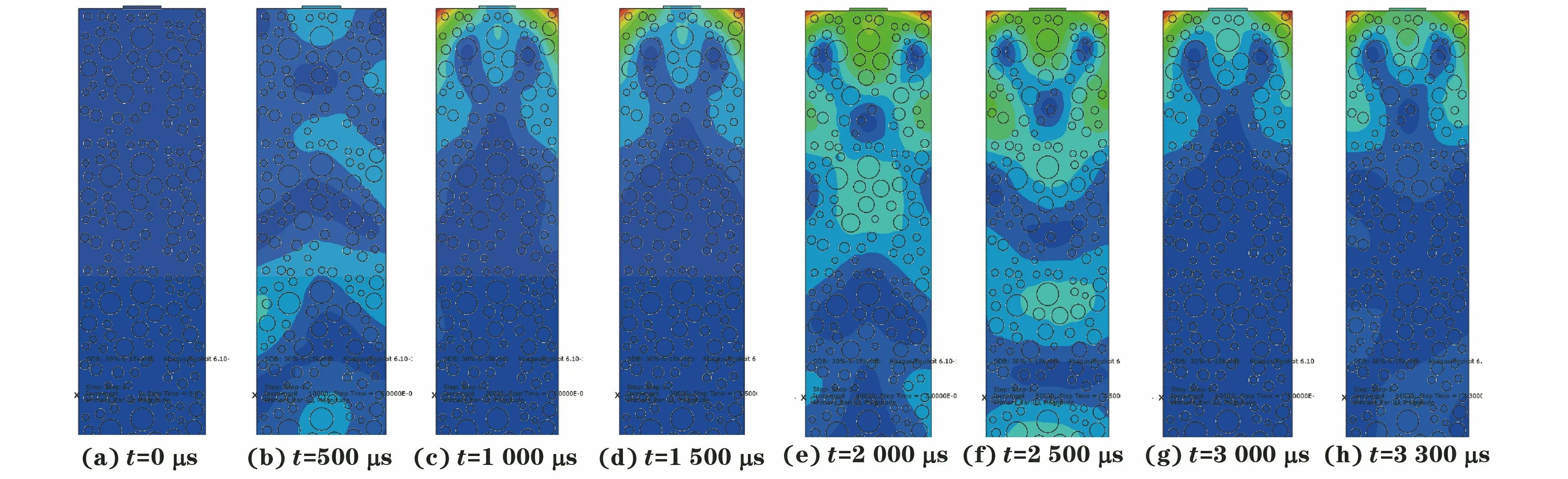
图6 骨料面积占比为30%的模型在各个时刻的响应云图

图7为不同激励频率下，不同骨料面积占比的模型的导波回波信号。

从图7可以看出，在相同的激励频率下，首波出现时间不随骨料面积占比的变化而发生变化，但信号的幅值和传播速度有明显的变化。图8所示为首波波峰与回波波峰的特征(出现时间和幅值)随骨料面积占比变化的趋势。

图8 首波波峰与回波波峰特征随骨料面积占比的变化趋势

通过分析各个参数的变化，可以得到以下结论。

(1) 在频散特性不明显的激励频段内，激励频率不变而骨料面积占比增大时，首波波峰的出现时间并不随之发生变化，但底端回波波峰的出现时间提前，且呈线性地提前了，这意味着导波传播的速度呈线性地变快。

(2) 激励频率不变而骨料面积占比增大时，混凝土的弹性模量逐渐增大，导致首波波峰和回波波峰的幅值都逐渐减小。

(3) 首波波峰和底端回波波峰的出现时间随着激励频率的升高而缩短，这意味着导波传播的速度不仅与材料特性有关，也与激励频率有关。

(4) 首波波峰和底端回波波峰的幅值随着激励频率的升高而降低，因为激励频率越大，波长越短，波的折射和反射现象越明显，衰减越大；激励频率越小，波长越长，波的折射和反射现象相对较弱，衰减越小。

以首波波峰出现时间和回波波峰出现时间之差作为传播时间，得到在频散现象较弱的激励频段内，不同激励频率下，不同骨料面积占比的模型中导波传播的速度变化曲线(见图9)。

图9 不同激励频率、不同骨料面积占比模型中导波传播的速度变化曲线

由图9可以得出以下结论。

(1) 在频散特性不明显的激励频段内，激励频率不变而骨料面积占比增大时，导波传播的速度呈线性变快的趋势。这是因为骨料含量的增大会使混凝土强度逐渐增大，试件的刚度也随之增大。

(2) 导波传播的速度随着激励频率的增大而减小。

为进一步分析骨料面积占比导致的导波回波信号的变化，放大信号的平稳段如图10所示，其最大幅值如图11所示。

图10 不同激励频率下不同骨料面积占比的信号平稳段

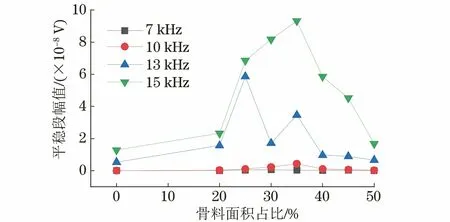
图11 不同激励频率下不同骨料面积占比的信号幅值变化曲线

由图11可见，对于同一激励频率，随着骨料面积占比的增大，信号平稳段的最大幅值先逐渐增大，后逐渐减小。这是因为骨料含量的增加会使得频散特性逐渐明显，而根据前文分析，骨料含量的增加会使得混凝土强度和刚度逐渐增大，回波信号的幅值会随之降低，在两者的共同作用下就出现了这样的现象。

为了对不同激励频率的导波回波信号进行分析，绘制如图12所示的不同激励频率下不同骨料面积占比的信号幅值变化曲线。

图12 不同激励频率、不同骨料面积占比的信号幅值变化曲线

由图12可知，在相同骨料面积占比下，随着导波信号激励频率的增大，频散特性的作用逐渐明显，表现为信号平稳段的最大幅值逐渐增大。

综上所述，激励频率不变而骨料面积占比增大时，首波波峰出现时间并不随之发生变化，但幅值会逐渐减小；底端回波波峰出现时间呈线性提前，幅值也会逐渐减小。激励频率发生变化时，首波波峰和底端回波波峰的幅值随着激励频率的升高而降低，导波传播的速度随之减小。在频散特性不明显的激励频段内，检测混凝土构件的导波回波信号在无缺陷情况下的信号平稳段幅值远小于激励信号段幅值和底端回波信号段幅值，可忽略不计。因此，缺陷检测的关键就是确定频散特性不明显的激励频段。

2 钢管混凝土构件轴向缺陷引起的导波回波信号变化

材料、应力和缺陷等均会对钢管混凝土构件中导波的传播产生影响，使导波发生折射和反射，导波的能量也随之衰减[7]。利用导波的这种特性来对钢管混凝土构件中的轴向缺陷进行检测。在ABAQUS软件中创建直径为100 mm的含轴向缺陷的钢管混凝土构件模型，并设置不同截面尺寸和轴向长度的缺陷。该节仅探究缺陷截面尺寸和轴向长度引起的导波回波信号的变化，缺陷位置固定在钢管混凝土模型中部。

将截面损伤定义为截面环形面积的缺失，首先对缺陷直径为10 mm的构件进行检测，不同长度缺陷的响应信号如图13所示。

图13 不同长度缺陷的响应信号(缺陷直径为10 mm)

由图13可知，信号平稳段对缺陷十分敏感，即使是截面损伤率仅为0.99%的情况下也可以很容易地判断出构件是否存在缺陷。对直径为10 mm的中心缺陷以及大径为30 mm、小径为20 mm的环形缺陷的信号平稳段的最大幅值进行统计，绘制其随缺陷长度的变化曲线，结果分别如图14，15所示。

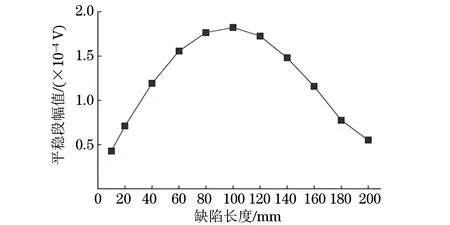
图14 中心缺陷信号幅值随缺陷长度的变化曲线

图15 环形缺陷信号幅值随缺陷长度的变化曲线

由图14,15可知，当缺陷截面尺寸一定时，随着缺陷轴向长度的增大，缺陷响应信号的平稳段的最大幅值先增大后减小。这是因为当缺陷轴向长度增大时，缺陷反射的信号幅值增大；随着缺陷轴向长度继续增大，缺陷周围界面反射波的相位差逐渐增大，当相位差超过半个汉宁窗的信号周期时，信号幅值符号相反，相互抵消，所以信号幅值下降。此外，不同长度的缺陷反射信号平稳段最大幅值相同时，可通过波形进行区分(见图16)。

图16 反射信号幅值相同但长度不同的缺陷波形

缺陷长度为10 mm的波形中间高两边低，而缺陷长度为200 mm的波形中间低两边高，这是信号叠加导致的，因此可以对两信号平稳段最大幅值相同而缺陷长度不同的情况进行区分。

3 结语

(1) 激励频率不变而骨料面积占比增大时，首波波峰出现时间并不随之发生变化，但幅值会逐渐减小；底端回波波峰出现时间呈线性提前，幅值也会逐渐减小。激励频率发生变化时，首波波峰和底端回波波峰的幅值随着激励频率的升高而降低，导波传播的速度随之减慢。在频散特性不明显的激励频段内，检测混凝土构件的导波回波信号中无缺陷情况下的信号平稳段幅值远小于激励信号段幅值和底端回波信号段幅值，可忽略不计。因此，缺陷检测的关键就是确定频散特性不明显的激励频段。

(2) 当缺陷截面尺寸一定时，随着缺陷轴向长度的增大，缺陷响应信号平稳段的最大幅值先增加后减小。