非极大弧连通定向图弧连通度的下界

王晓丽,张雪霞

(晋中学院 数学系，山西 榆次 030619)

0 引言

对任何一个有向图，它的弧连通度λ与最小度δ满足λ≤δ，当λ=δ时， 称有向图D是极大弧连通的,说明最小度δ是弧连通度λ的上界.Chartrand 和Harary已经对图的点连通度的下界进行了研究.Topp和Volkmann得出了二部图相似的下界.但对于非极大弧连通图的弧连通度的下界结论很少.本文考虑定向图D满足团数ω(D)≤p时，把无向图的Turán定理的结论推广到定向图，利用函数的凸性来研究定向图的弧连通度，得出了非极大弧连通定向图弧连通度的下界.本文未给出的术语和记号请参见文献[1].

1 预备知识

定义1[1]顶点v的度

d(v)=min{d+(v),d-(v)}，

其中d+(x)和d-(x)分别表示顶点v的出度和入度.

定义2[1]没有2-圈且没有环的有向图称为定向图.

定义3[1]有向图D的最小度

δ=min{δ+,δ-}，

其中δ+和δ-分别表示D的最小出度和最小入度.

定义4[2]如果去掉有向图D的弧的方向，再去掉产生的重边得到的简单图UG(D)不含p+1个顶点的团，称有向图D的团数ω(D)≤p.

定义5[2]若n阶有向图D的顶点集为{v1,v2,…,vn}，有向图D的度序列定义为顶点度的不增序列(d1,d2,…,dn)，即d1≥d2≥…≥dn=δ.

引理1[3](Turán定理)设整数p≥1,若图G不含完全子图Kp+1，则

引理2[4]f(x)是[L,R]上的连续凸函数，若l,r∈[L,R]，满足l+r=L+R，则

f(L)+f(R)≥f(l)+f(r).

2 主要结论

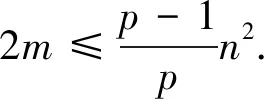
证明因为D是定向图，所以D的弧数与UG(D)的弧数相等，即

m(D)=m(UG(D))=m.

又因为D的团数ω(D)≤p，所以ω(UG(D))≤p.由引理1知，

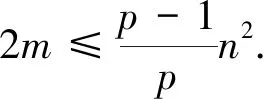
定理2若D是团数ω(D)≤p的n阶定向图，任取顶点集S⊆V(G),|S|=k,则

证明(1)若UG(D[S])不含p个顶点的团，则

(2)若UG(D[S])包含p个顶点的团，取顶点集Q⊆S,UG(Q)是不包含p个顶点的团的顶点数最多的顶点集.设|Q|=l,则D的每个顶点的邻集的导出子图不包含p个顶点的团.假设D的顶点v1的邻集的导出子图包含p个顶点的团，则UG(D)包含p+1个顶点的团，与定向图D的团数ω(D)≤p矛盾，所以D的每个顶点的邻集的导出子图不包含p个顶点的团.

|N(v1)|>l，

则N(v1)不包含p个顶点的团，但|N(v1)|>l，与顶点集Q的选取矛盾，所以v在S中最多有l个邻点.

则

因此

证明令φp(k,x)=

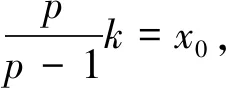
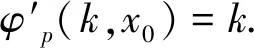
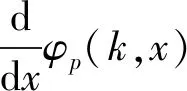
定理4设D是一个团数W(D)≤P的n阶强连通定向图,D的不增度序列为(d1,d2,…,dn)，若λ<δ，则

其中

1≤k≤a,a=max2δ+1,2pδp-1{}.

证明因为λ<δ，故存在两个不相交的集合X,Y⊆V(D),满足X∪Y=V(D),|(X,Y)|=λ<δ,使得|X|、|Y|≥2δ+1[2].

(反证法)假设X,Y⊆V(D)满足X∪Y=V(D)且|(X,Y)|=λ<δ,使得|X|≤2δ.

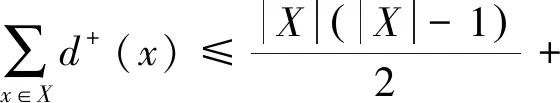
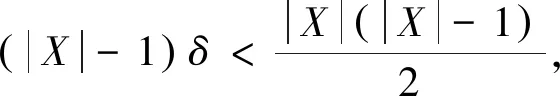
同理可证|Y|≥2δ+1.

将X、Y中的顶点按顶点度从大到小排列，选S，T分别是排好序后的X，Y中前k个顶点组成的集合.其中

1≤k≤a,a=max2δ+1,2pδp-1{}.

由于定向图D不含p+1个顶点的团，所以D[X],D[Y]也不含p+1个顶点的团.

在D[X],D[Y]中，由定理2知

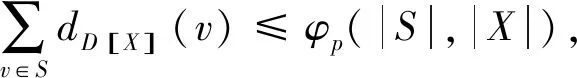
因此

同理

故

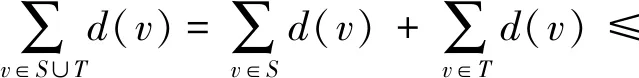
由S、T的选取知S∪T包含D的k个最高度顶点，但不含D的a-k个最低度的顶点.

即

推论设D是一个团数W(D)的n阶强连通定向图,D的不增度序列为(d1,d2,…,dn)，若λ<δ，则

证明由定理4，k=1时，

3 结语

本文利用函数的凸性研究了定向图的弧连通度.当定向图D满足团数ω(D)≤p时，分析弧连通度与度序列之间的关系，得出非极大弧连通定向图弧连通度的下界，也可以利用函数的凸性研究定向图极大和超级弧连通的度序列条件.