由扇形制成多个圆锥的体积之和
——Jensen不等式的一个几何应用
深圳市龙华区教育科学研究院附属外国语学校(518109) 钟文体
取一个圆,剪出两个扇形,再围成两个圆锥.如何剪能使两个圆锥的体积之和最大? 文[1]提出并解决了这个问题,其解答涉及一个三次方程的求解.文[1]的末尾还提出了这样一个问题:对一般的扇形,如何分成两个或多个扇形,使围成的两个或多个圆锥的体积之和最大? 本文使用Jensen 不等式部分地解决这个问题.
首先回顾凸函数的概念.
设f(x)是定义在区间I上的函数,若对任意x1,x2∈I及任意λ ∈(0,1),有f(λx1+(1−λ)x2) ≤λf(x1)+(1−λ)f(x2),则称f(x)为I上的凸函数.若等号成立当且仅当x1=x2,则称为严格凸函数.
关于凸函数,有著名的Jensen 不等式.
Jensen 不等式设f(x) 是I上的凸函数,若xi ∈ I,qi >0(i= 1,2,··· ,n) 且= 1,则f(q1x1+q2x2+···+qnxn)≤q1f(x1)+q2f(x2)+···+qnf(xn).若f(x) 为严格凸函数,则等号成立当且仅当x1=x2=···=xn.下面的引理可以很方便地判断给定函数是否为凸函数.
引理设f(x)在区间I上有二阶导数,且对∀x ∈I,有f′′(x) ≤0,则f(x)是I上的凸函数.若不等号严格成立,则为严格凸函数.有了这些准备,我们可以证明下述结论.
命题设扇形的半径为R,圆心角θ≤187.5°.将这个扇形分成n个小扇形,再围成n个圆锥.则当这n个小扇形的圆心角相等时,所围成n个圆锥的体积之和取最小值当这n个小扇形中有一个的圆心角趋于θ,其余的圆心角趋于0 时,所围成n个圆锥的体积之和趋于.且不管怎么分,所围成的圆锥体积之和都不超过
证明设小扇形的圆心角分别为αi(i= 1,2,··· ,n),所围成的圆锥的底面半径为ri,则α1+α2+···+αn=θ,Rαi= 2πri.故ri=圆锥的母线长都为R,故高分别为hi=于是,圆锥的体积之和为
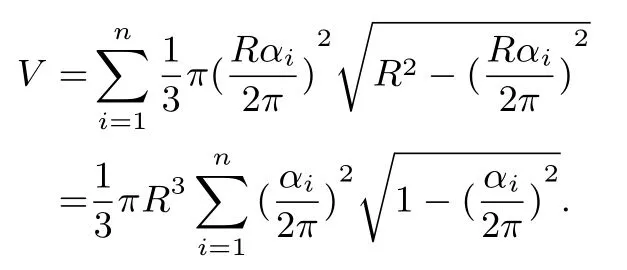
考虑函数f(x) =ai,则V=简单的计算得f′(x) =从而f′(x)>0⇔x ∈ f′′(x)>0⇔x ∈于是f(x)在上严格递增,在上严格凸.
由条件可知ai∈故由Jensen 不等式,有等号成立当且仅当a1=a2=···=an,即当且仅当α1=α2=···=αn.从而
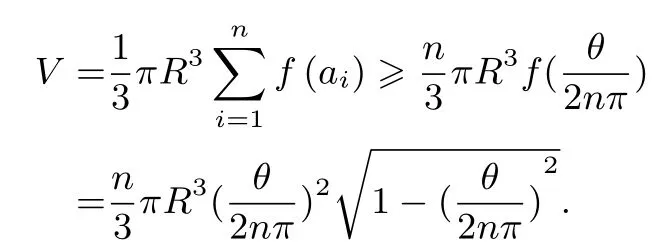
另一方面,设xi且x1+x2+···+xn≤我们证明f(x1)+f(x2)+···+f(xn) ≤f(x1+x2+···+xn),且等号成立当且仅当x1,x2,··· ,xn中有n −1 个为零.用数学归纳法.设n= 2.当x1,x2中有一个为零时,结论显然成立.不妨设0̸=x1≤x2.考虑函数g(x) =f(x1+x)−f(x),x ∈
求导得g′(x) =f′(x1+x)−f′(x).因x,x1+x ∈由前面的论述可知f′(x) 在上严格递增,故g′(x) =f′(x1+x)−f′(x)>0.
于是,g(x)在上严格递增.从而g(x) ≤g(0),即f(x1+x) ≤f(x1)+f(x),且等号成立当且仅当x= 0.特别地,f(x1+x2)> f(x1)+f(x2).故n= 2时,结论成立.
假设n=k时,结论成立,即f(x1) +f(x2) +···+f(xk)≤f(x1+x2+···+xk).那么,n=k+1 时,
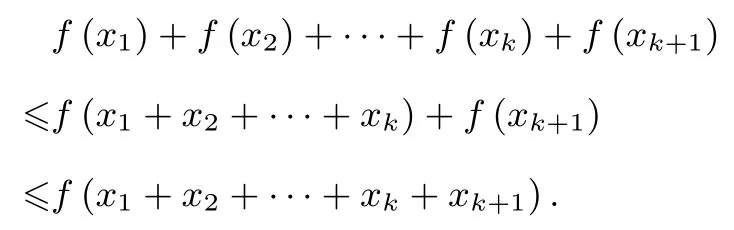
根据归纳假设,第一个等号成立的条件为x1,x2,··· ,xk中有k−1 个为零;第二个等号成立的条件为x1+x2+···+xk和xk+1中有一个为零.由此不难得到上述不等式中等号成立的条件为x1,x2,··· ,xk+1中有k个为零.从而结论成立.特别地,有
注1圆心角θ >时如何处理是个值得思考的问题,留给读者作进一步的思考.
注2可以证明n增大时,最小值
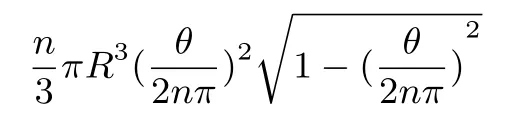
———《扇形的认识》教学廖

