结合导数中的构造问题谈一题多解与多题一解

广东省东莞市东莞中学(523005) 卢 众

在复习阶段,题目千变万化,解法也是多样.如何让学生脱离题海,提高学习的效率,是大部分老师与同学都面临的问题.本文以导数中的构造问题为载体,通过分析题干,探寻问题的关键,进而找到各种解法.并总结提升,寻求通法,提供几点有益于教学的建议.

一、问题呈现

题目1定义在R 上的奇函数y=f(x) 满足:当f(−1) = 0 且x >0 时,xf′(x)< f(x).求不等式f(x)>0的解集.

解法1(构造特殊函数) 令f(x) =−x3+x,易知y=f(x)满足题意,则f(x)>0 的解集为(−∞,−1)∪(0,1).

分析构造f(x)=−x3+x的过程较为困难,并不是每个同学都能够掌握.不妨尝试从“x >0 时xf′(x)< f(x)”这个条件出发,令f(x) =ax+b,则由xf′(x)< f(x)可知b>0.不妨令b=1,因为f(1)=−f(−1)=0,所以a=−1,f(x)=−x+1.又y=f(x)为R 上的奇函数,所以

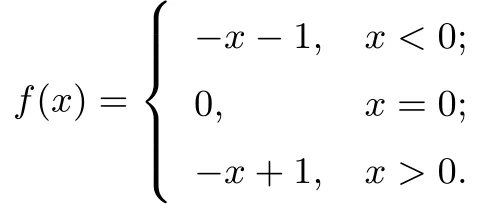
从而,f(x)>0 的解集为(−∞,−1)∪(0,1).

解法2(构建抽象函数模型)令F(x) =所以x>0 时,F′(x)=<0,则y=F(x)在(0,+∞)上单调递减.又因为F(1) ==f(−1) = 0,所以x >0 时,若f(x)>0,即F(x)>0,则x ∈(0,1).由y=f(x) 为奇函数可知,y=F(x) 是(−∞,0)∪(0,+∞)上的偶函数,所以x <0 时,若f(x)>0,则F(x)<0,x ∈(−∞,−1).又因为f(0) = 0,所以f(x)>0 的解集为(−∞,−1)∪(0,1).

分析根据导数结构的特征“xf′(x)

题目2定义在R 上的函数y=f(x)满足f(0)=2,且f(x)+f′(x)>1,求不等式exf(x)>ex+1 的解集.

解法1(构造特殊函数法)易知f(x) = 2 满足题意,由exf(x)>ex+1 可知解集为(0,+∞).

分析函数f(x) = 2,符合题意,且易于解题,显示出此解法的简便之处.此题也可尝试设f(x) =ax2+b(a ̸= 0),则f(0) =b= 2,f(x)+f′(x) =ax2+2ax+b >1,即ax2+2ax+1>0 恒成立,则a>0 且∆=4a2−4a<0,所以+2 符合题意.若exf(x)>ex+1,则则所以y=F(x)在R 上单调递增.由F(0) = 0,若F(x)>0,则x >0,即exf(x)>ex+1的解集为(0,+∞).

解法2(构建函数模型) 令F(x) = ex(f(x)−1),则F(0) = e0(f(0)−1) = 1.因为F′(x) = ex(f(x)+f′(x)−1)>0,所以y=F(x)在R 上单调递增.由exf(x)>ex+1,得到F(x)>1=F(0),则解集为(0,+∞).

分析先根据“f(x) +f′(x)”的结构特征,构造抽象函数G(x) = exf(x).再结合G′(x) = ex(f(x) +f′(x))以及题设f(x) +f′(x)−1>0,调整y=G(x) 并构造F(x)=G(x)−ex,则F′(x)=ex(f(x)+f′(x)−1)>0 符合题意.

题目3 (2013年高考辽宁卷理科第13 题)若函数f(x)满足x2f′(x)+2xf(x)=则x>0 时,f(x)( ).

A.有极大值、无极小值 B.无极大值、有极小值

C.既有极大值又有极小值 D.既无极大值也无极小值

解令F(x) =x2f(x)−H(x),其中y=H(x) 满足H′(x) =因为F′(x) = 0,所以F(x) =C,其中C为任意常数,从而f(x) =且H(2) =4f(2)−C=−C.因为f′(x) =令u(x) = ex −2H(x)−2C,则u′(x) =所以y=u(x)在(0,2)上单调递减,在[2,+∞)上单调递增.因为u(2) = e2−2H(2)−2C= 0,u(x) ≤u(2) = 0,所以x ∈(0,+∞) 时,f(x) ≤0,y=f(x) 在(0,+∞) 上单调递增,y=f(x)在(0,+∞)上既无极大值又无极小值,答案为D.

分析此题先根据“xf′(x) + 2f(x)”构造G(x) =x2f(x).再 结 合G′(x) =x(xf′(x) + 2f(x)) 以 及 题 设xf′(x) + 2f(x)−= 0,调整y=G(x) 并构造函数F(x) =G(x)−H(x) =x2f(x)−H(x),其中y=H(x)满足H′(x) =因为F′(x) =x(xf′(x)+2f(x)−=0,则F(x)=x2f(x)−H(x)=C.

二、通法探究

(一)构造特殊函数法

此方法在于根据题目条件,选择符合题意的特殊函数y=f(x)解题,常见困难为:(1)题设条件较多,难以找到符合所有条件的函数;(2)构建的函数过于复杂,不利于解决问题.因此解决问题时,应从简单的函数(或其复合结构)逐步尝试,且对各条件的意义以及重要程度分析,选择合适的方式逐一处理.常见的问题与处理办法有:①利用待定系数法解决特殊点的问题; ②可考虑构造分段函数解决奇偶性问题.

这种方法虽不够严谨,但在选择填空题中,却往往能够表现得较为灵活.

(二)构建函数模型

该方法相对构造特殊函数的方法而言,更具有适用性,可以解决更多类型的问题.其基本步骤如下:

1.观察导数的结构特征“xf′(x)±mf(x)”,“f′(x)±mf(x)”,构造抽象函数“F(x) =xmf(x)”或“F(x) =ef(x)”,必要时,再结合导数结构的其他特征修正函数y=F(x);

2.根据原函数y=f(x)的性质,推导函数y=F(x)的性质,并画出函数y=F(x)的大致图像;

3.将问题转化为与函数y=F(x)相关的问题;

4.借助y=F(x)的性质与图像解决问题.

三、教学思考

一题多解可以体现解法的多样,串联知识点的各个性质,提升对问题的迁移能力,让学生的思维有一个更开阔的空间,在解决问题时,能有效的避免思维短路.同时也能对各种方法产生明显的对比,分析其优劣,便于在应用时选择最高效的方法.但不足的是,方法较多,容易对每一种方法掌握不透彻,应用不熟练.

多题一解侧重在对通法的探究,容易对知识点理解透彻,即便面对不同问题,也容易找到问题的关键,举一反三,触类旁通.

因此在复习阶段,应从学生情况出发,两者灵活应用,才能互相弥补.在一题多解的基础上,找通法,能够对各种方法掌握更透彻,并找到典型的解法,对基础薄弱的同学更为适用.而在多题一解的基础上进行一题多解,拓展学生思维,让理解和思维能力达到更高的台阶,对基础好的同学更为有用.因此在班级教学中,面临不同层次的学生,为了更有效的进行层次教学,两种教学观念都应重视.