与椭圆有关的斜率之积为定值的几个命题*

山东省泰安市宁阳县第一中学(271400) 刘才华

在与椭圆相关的综合型问题中,有这样一类问题,题目中含有条件“对于椭圆上两点P,Q,O为坐标原点,满足此类问题一般的解题思路需要将直线方程和椭圆方程联立方程组,通过消元化归为一元二次方程,再利用韦达定理进行较为复杂的运算给出解答.我们在解答这些题目的时候,通过观察探究和整体运算求解发现,具有上述条件的椭圆有着一些特殊的结论,并且结论之间有着相互的内在联系.本文从点的坐标间的关系、线段长度间的关系和直线斜率间的关系三个角度出发,得到如下几个优美的命题.

命题1如图1,椭圆= 1(a > b >0)上有两点P(x1,y1),Q(x2,y2),O是坐标原点,若直线OP,OQ的斜率满足kOP · kOQ=则

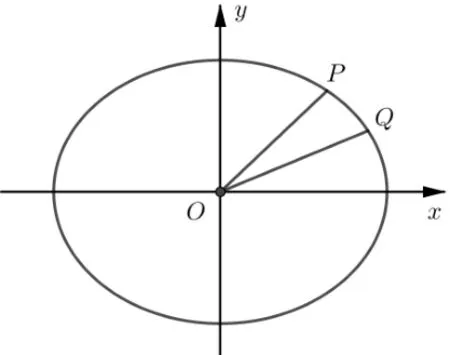
图1

证明由= 1 得同理有由kOP · kOQ=则由

命题1 给出了一条坐标间的定值性质:满足条件的两点间横坐标的平方和与纵坐标的平方和均为定值.

命题2如图1,椭圆= 1(a > b >0)有两点P(x1,y1),Q(x2,y2),O是坐标原点,若直线OP,OQ的斜率满足kOP ·kOQ=则x1y1=x2y2.

证明由命题1 得得同理有由,则于是

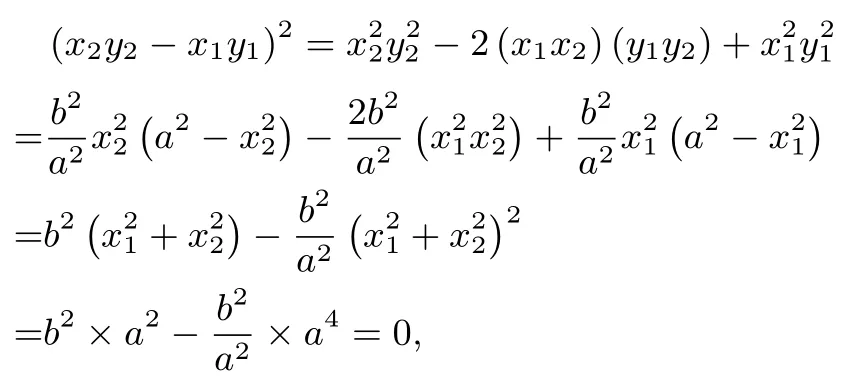
故x1y1=x2y2.

命题2 给出了满足条件的两点间对应坐标乘积间的关系.

通过探究条件中与点P,Q相关的线段长度间的关系,我们得到

命题3如图1,椭圆=1(a>b>0)上有两点P(x1,y1),Q(x2,y2),O是坐标原点,若直线OP,OQ的斜率满足kOP ·kOQ=则|OP|2+|OQ|2=a2+b2(定值).

证明设P(x1,y1),Q(x2,y2),由命题1 得则|OQ|2=a2+b2(定值).

命题3 给出了一条定值性质:满足条件的两条线段长度的平方和为定值.

命题4如图2,四边形ABCD内接于椭圆1(a > b >0),且AC,BD相交于坐标原点O,若直线OA,OD的斜率满足kOA·kOD=则|AB|2+|BC|2+|CD|2+|DA|2=4(a2+b2)(定值).

证明由命题3 得|OA|2+|OD|2=a2+b2.

由椭圆的对称性知四边形ABCD为平行四边形.由平行四边形的四条边长的平方和等于对角线长的平方和得|AB|2+|BC|2+|CD|2+|DA|2=|AC|2+|BD|2=4(|OA|2+|OD|2)= 4(a2+b2),故|AB|2+|BC|2+|CD|2+|DA|2=4(a2+b2)(定值).

命题4 给出了一条定值性质:由满足条件的两条线段生成的平行四边形中四条边长的平方和为定值.

通过探究条件中与点P,Q相关的直线斜率间的关系,我们得到

命题5如图1,椭圆= 1(a > b >0)上有两点P(x1,y1),Q(x2,y2),O是坐标原点,若直线OQ,OP的斜率满足kOP ·kOQ=则

证明由命题1 得由kOP ·kOQ=由斜率公式得

命题5 给出了一条斜率性质:kP Q为kOP和kOQ的等比中项.

命题6如图2,四边形ABCD内接于椭圆1(a > b >0),且AC,BD相交于坐标原点O,若直线OA,OD的斜率满足kOA·kOD=则kAB+kAD=0.

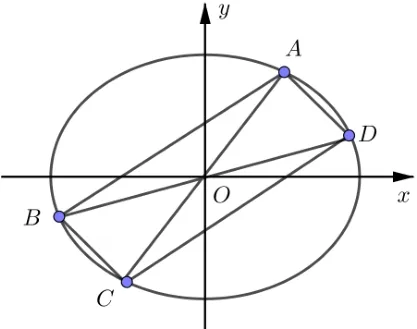
图2

证法 1设A(x1,y1),B(x2,y2),则由题意得D(−x2,−y2),则kAB+kAD=由命题2 得x1y1=x2y2,故kAB+kAD=0.

证法2由题意得kOA ·kOB=kOA ·kOD=由命题5 得由于kAB与kAD一正一负,故kAB+kAD=0.

命题6 给出了一条斜率性质:由满足条件的两条线段生成的平行四边形中,两条邻边所在直线的斜率为互为相反数.