素养导向指引下例谈圆锥曲线焦点三角形问题的解题策略*

福建省南平市高级中学(353000) 江智如 李寿滨 黄丽群

圆锥曲线焦点三角形问题是高考与各类模拟考试的热点题型,涵盖几何、向量、三角、函数等多领域的知识与方法,综合性强,思维强度高,是圆锥曲线知识的重点与难点,考查考生数学阅读能力、数形结合思想、化归与转化思想、推理论证能力与运算求解能力.这类问题一般考查角度、周长、面积、中位线、角平分线、离心率等问题[1],包含丰富的圆锥曲线性质知识,解题策略多样,方法巧妙,需要从不同的角度针对问题条件进行策略选择,全方位反映焦点三角形问题的几何特征,引导学生掌握运用代数语言把几何问题转化为代数问题的思想与方法,提升直观想象、数学运算、数学建模、逻辑推理和数学抽象素养[2],有助于学生将高中数学基本知识结构化、系统化,形成学科知识网络[3].本文从高中学生的认知水平出发,把焦点三角形问题归纳为六种类型,在学科素养的指引下,探究问题解决的有效思路与方法.

1 概念界定

如图1 与图2,椭圆或双曲线上的一点P,与两焦点所构成的∆F1PF2称为椭圆或双曲线的焦点三角形.本文研究的圆锥曲线焦点三角形问题界定为:结合椭圆或双曲线的几何性质,解决与焦点三角形相关的问题,主要包括周长、离心率、角度、面积、中位线、角平分线等问题.

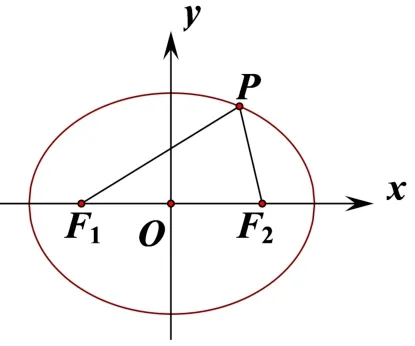
图1

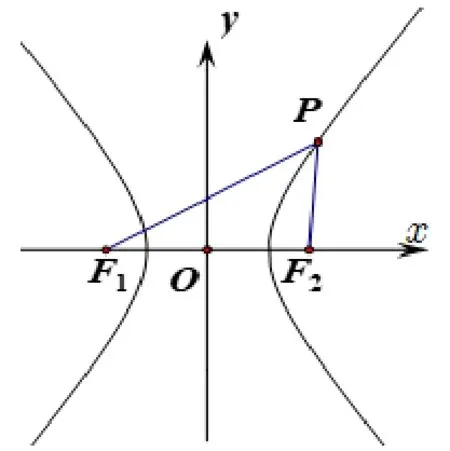
图2

2 方法探究

圆锥曲线焦点三角形问题主要围绕圆锥曲线的几何性质展开,利用正余弦定理、平面向量、平面几何等相关知识与结论,借助数形结合思想,转化为圆锥曲线的性质或解三角形题型,运用函数与方程思想、建模思想,通过扎实的运算求解能力,解决问题,常采用四种解题方法:(1)定义法;(2)解析法;(3)三角法;(4)向量法.

3 方法应用

3.1 周长问题

周长问题常考虑定义法,解题思路为:从圆锥曲线的第一定义出发,利用三角形的三边长关系与对称性质转化为共线问题,确定特殊点位置,结合正余弦定理和平面向量方法求解.要求考生具有扎实的几何功底,体现数学学习的能力与潜能[4].

题目1(2015年高考全国I 卷文科第16 题)已知F是双曲线C:x2−= 1 的右焦点,P是C左支上一点,当∆APF周长最小时,该三角形的面积为____.

分析本试题是以周长问题为背景寻找点P的位置,求解三角形面积问题.由已知条件可设左焦点为F′(−3,0),因为点P在C的左支上,所以由双曲线第一定义可得∆APF的周长|AP|+|AF|+|PF|=|AP|+|AF|+|PF′|+2a≤|AF|+|AF′|+2a,当且仅当A,P,F′三点共线且P在A,F′中间时取等号,此时直线AF′的方程为=1,联立双曲线方程得再由面积割补法求得,∆APF的面积为考查数形结合思想、推理论证能力和运算求解能力.

3.2 离心率问题

离心率是圆锥曲线的重要性质,常以选填题形式出现,常考常新,考查考生圆锥曲线知识掌握水平和综合应用能力.解题的思路是:根据已知条件探寻a,b,c三者之间的关系,要求考生运用圆锥曲线第一定义、正余弦定理、不等式等知识分析和探寻解题方向,通过细心的运算,步步为营,得到最终结果,培养考生数学素养,提高考生的圆锥曲线综合应用能力.

题目2(2018年高考全国II 卷理科第12 题)已知F1,F2是椭圆C:= 1(a > b >0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,∆PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为( )

分析本试题中P点虽然不在椭圆C上,但问题本质仍然是焦点三角形题型,解题的关键可以由∆PF1F2为等腰三角形及∠F1F2P= 120°确定点P的位置,即PF2=F1F2= 2c.再由AP的斜率为得到tan ∠PAF2=考虑把问题转化到∆PF1F2中,利用正弦定理确定角与边的关系,即其中sin ∠APF2=而sin ∠PAF2=cos ∠PAF2=可 求sin ∠APF2=所以化简得a= 4c,故e=考查考生综合运用所学知识解决问题的能力,实现考查阅读、应用、建模能力的目的[5].

3.3 角度问题

角度问题需要运用椭圆或双曲线的第一定义,借助正余弦定理或向量夹角,转化为焦半径|PF1|、|PF2|与焦距|F1F2|之间的数量关系,再利用函数或不等式方法求解问题.解决思路为:设∠F1PF2=θ,则

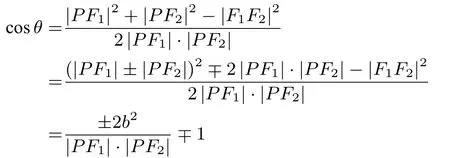
其中|PF1| · |PF2|可由基本不等式或函数方法求解取值范围,再根据题设条件得到θ取值范围.特别地,当|PF1|=|PF2|时,等号成立,此时点P为椭圆短轴或双曲线虚轴的端点,θ取到最大.

题目3(2017年高考全国I 卷文科第12 题)设A、B是椭圆= 1 长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )

分析本试题中A、B两点是长轴的两个端点,根据椭圆的对称性质,考虑类比焦点三角形的角度结论可以得到,当点M为椭圆短轴的端点,∠AMB取到最大,此时有∠OMB≤60°.因为已知条件没有明确椭圆焦点的位置,所以对参数m进行讨论:当0< m <3 时,即0< m≤ 1; 当m >3 时,b=tan ∠OMB=≤tan 60°=即m≤9; 综上所述,m ∈(0,1]∪[9,+∞).考查考生对椭圆性质知识的理解与应用水平,体现试题的基础性与选拔功能.

3.4 面积问题

面积问题主要运用解析法、三角法和向量法求解,解决思路为:转化为|PF1|、|PF2|、|F1F2|或a,b,c及角∠F1PF2=θ之间的数量关系,借助三角函数知识与圆锥曲线性质求解.特别地,在椭圆或双曲线中,∆F1PF2的底边为定值2c,|PF1|,|PF2|及∠F1PF2=θ为变量,可以推导椭圆中焦点三角形的面积为S=b2tan双曲线为S=

题目4(2019年高考全国II 卷文科第20 题)已知F1,F2是椭圆C:=1(a>b>0)的两个焦点,P为C上一点,O为坐标原点.

(1)若∆POF2为等边三角形,求C的离心率;

(2)如果存在点P,使得PF1⊥PF2,且∆F1PF2的面积等于16,求b的值和a的取值范围.

分析本试题依托三角形背景知识考查离心率和参数取值范围问题,考虑运用定义法和向量法求解.第(1)问面向大部分考生,首先连结PF1,由∆POF2为等边三角形可知,在∆F1PF2中,∠F1PF2= 90°,于是把问题转化为直角三角形,可求|PF2|=c,|PF1|=再由椭圆的第一定义知,2a=|PF1|+|PF2|=所以C的离心率是考查直观想象能力与运算求解能力;

第(2)问根据焦半径垂直关系,把面积问题转化为动点的坐标运算.设点P(x,y),则有又PF1⊥PF2,故= 0,从而x2+y2=c2,联立= 1,化简得y2=所以求得b= 4.把y2=代入= 1,得x2=所以c2≤b2,从而a2=b2+c2≤2b2= 32,故a≤即当b= 4,时,存在满足条件的点P.因此b=4,a的取值范围为此处考查考生椭圆知识掌握与应用水平,展现考生分析问题、解决问题的思维过程[6],体现试题的选拔与区分功能.

3.5 中位线问题

中位线问题运用定义法,利用三角形中位线性质,化归转化为圆锥曲线第一定义求解.解题思路为:在圆锥曲线中,若点M为线段PF1的中点,连接OM,因为点O为F1F2的中点,所以在∆PF1F2中,有OM//PF2且OM=从而把OM转化为PF2,即把点M的位置问题转化为点P的位置问题求解,考查逻辑思维能力和创新能力.

题目5(2020年福建南平高三期末质检15)如图3,已知F1,F2是双曲线C:=1(a,b>0)的左、右焦点,若双曲线右支上存在点P,使得以双曲线实轴为直径的圆与线段PF1相切于线段PF1的中点M,则双曲线C的离心率为____.

图3

分析本试题以圆的切线和三角形中位线背景知识,考查离心率问题,考虑利用圆的切线和中位线性质,把问题转化为双曲线的第一定义,探寻a,c之间关系求解.为此连接PF2,可得在∆PF1F2中,有OM//PF2且又PF1与圆O相切于点M,故OM⊥PF1,从而PF2= 2OM= 2a且PF1⊥PF2,所以由双曲线第一定义可知,PF1= 4a.在Rt∆PF1F2中,由勾股定理得,PF21+PF22=F1F22,即(4a)2+(2a)2= (2c)2,解得体现考生将所学知识迁移到新情境,解决新问题的能力[3],培养考生数学建模能力和创新能力.

3.6 角平分线问题

角平分线问题是通过三角形的内角平分线性质,利用正弦定理把角的关系转化为对应边的比值,结合圆锥曲线第一定义求解.解题思路为:在∆PF1F2中,若∠F1PF2的平分线为PM,交F1F2于点M,则有从而把动点P转化为点M,而点M、F1、F2共线,再根据已知条件求解问题.考查考生数学综合能力与学习潜能,引导考生打破常规进行思考,自主发现问题,提出解决方案,作出独立的判断和解答,创造性地解决问题[6].

题目6(2011年高考全国II 卷理科第15 题)已知F1,F2是双曲线C:= 1 的左、右焦点,点A在双曲线C上,点M的坐标为(2,0),AM为∠F1AF2的角平分线,则|AF2|=____.

分析本试题点M在x轴上,考虑运用内角平分线性质把问题转化为点M、F1、F2共线,即在∆F1PF2中,由AM为∠F1AF2的平分线可得,所以点M在双曲线的右支,从而由双曲线第一定义知,|AF1|−|AF2|= 2a= 6,联立得|AF2|= 6.此题考查考生数学阅读理解能力,强化推理论证,考查理性思维能力,激发考生学习兴趣,提高考生学习的热情,有助于创新问题的解决[6].

4 方法总结

圆锥曲线焦点三角形问题依托圆锥曲线定义与性质知识,考查考生解析几何功底和数学综合应用能力.考生可以通过目标分析、问题转化、模式识别进行求解,利用正余弦定理、向量性质、勾股定理等知识,把问题转化为圆锥曲线第一定义求解.引导考生深刻认识圆锥曲线的第一定义及丰富的几何特征,巩固复习已学知识,渗透解题策略多元化的思想.在日常的教学过程中,教师可以设计相应的“精致练习”[7],帮助学生巩固与深化所学知识,构建圆锥曲线知识网络结构,提高解题技巧及分析问题、解决问题的能力,增强思维的灵活性,培养学生求异创新的发散思维,实现学生数学学科素养的提升.