内配螺旋箍筋方钢管高强混凝土柱的轴压试验

林佳鑫， 王浩祚， 邓杨鹏， 胡红松,2

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 华侨大学 福建省结构工程与防灾重点实验室， 福建 厦门 361021)

相较于圆钢管混凝土(CFST)柱，方钢管混凝土柱对内填混凝土的约束能力较弱，因此，方钢管混凝土柱的抗变形能力小于圆钢管混凝土柱.此外，当内填混凝土采用高强混凝土时，方钢管混凝土柱的抗变形能力将进一步减弱，这对承受地震作用的结构构件极为不利.为了提高方钢管混凝土柱及內填高强混凝土柱的抗变形能力，学者们已经提出了许多技术措施，例如，在钢管混凝土柱中内置螺旋箍筋，从而提高抗变形能力.

基于此，本文对内填混凝土强度为112 MPa的3个内配螺旋箍筋方钢管混凝土试件和1个方钢管混凝土对比件进行单调轴压加载，对SCCFST试件的轴压承载力、峰值后性能和破坏模式进行研究.

1 试验方案

1.1 试件设计

图1 内配螺旋箍筋方钢管混凝土柱的构造(单位:mm)Fig.1 Construction of square SCCFST columns (unit: mm)

试验共设计4个方钢管混凝土柱试件，包含3个内配螺旋箍筋方钢管混凝土柱(编号为UC-N-2.0，UC-H-2.0，UC-H-2.9，H，N分别表示内配螺旋箍筋母材为高强钢筋和普通钢筋,数字表示内配螺旋箍筋试件的体积)和1个方钢管混凝土柱(编号为UC-O).试件的外包方钢管都是由厚度为5.6 mm的钢板焊接而成，方钢管的截面宽度和高度分别为200，600 mm.

内配螺旋箍筋方钢管混凝土柱的构造,如图1所示.图1中：试件上、下端板100 mm范围内为螺旋箍筋的加密区，加密区的箍筋间距为对应中部区的一半，以保证破坏不发生在试件的端部.

试件主要参数，如表1所示.表1中：D为箍筋约束区的直径；dsp为螺旋箍筋的直径；Asp为螺旋箍筋的横截面积；s为箍筋间距;fyp为螺旋箍筋的屈服强度；ρs为螺旋箍筋的体积配箍率(ρs为1.95%～2.94%)，其定义为

(1)

表1 试件的主要参数Tab.1 Main parameters of specimens

1.2 材性实测

钢材的应力-应变(σ-ε)曲线，如图2所示.图2中：钢板的厚度为5.6 mm；普通钢筋和高强钢筋的直径均为8 mm.由于高强钢筋的应力-应变曲线没有明显的屈服平台段，故将塑性应变为0.2%时对应的应力值作为名义屈服极限.

图2 钢材的应力-应变曲线 Fig.2 Stress-strain curves of steel

钢板、普通钢筋和高强钢筋的材性性能，如表2所示.表2中：Es为弹性模量；fy为屈服强度；fu为极限强度；η为断后伸长率.

采用內填混凝土的圆柱体抗压强度设计值为110 MPa的高强混凝土，并制作8个同批次的圆柱体(150 mm×300 mm(直径×高))试块，所有试块在相同的环境下进行密封养护，测得试验中内填混凝土圆柱体抗压强度为112 MPa.

表2 钢材的材性性能Tab.2 Material properties of steel

1.3 加载方案及量测

试验的加载装置和测点布置，如图3所示.采用10 MN电液伺服控制压力机对试件进行单调轴压加载.为测量试件的轴向压缩量，沿试件四周布置4个位移传感器(LVDT)；钢管的4个侧面各粘贴1个应变片；内配螺旋箍筋试件的螺旋箍筋上均布置8个应变片，其中，箍筋中部区布置6个应变片，端部加密区布置2个应变片.

采用位移控制的加载制度，位移加载速度参照每秒轴向应变增长2.0×10-5的速率进行连续加载，加载至轴向应变为5%或外包方钢管的竖向焊缝开裂时，停止加载.

(a) 加载装置 (b) 测点布置 图3 试验的加载装置和测点布置(单位：mm)Fig.3 Loading device and measuring point arrangement of test (unit: mm)

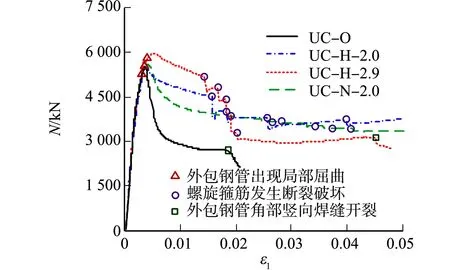
图4 试件的轴力-轴向应变曲线Fig.4 Axial load-axial strain curves of specimens

2 实验结果与分析

2.1 轴力-轴向应变曲线

试件的轴力-轴向应变(N-ε1)曲线，如图4所示.由图4及相关计算可知：4条曲线的上升段基本相同且近似呈直线状，无明显拐点；当轴向应变超过2%后，试件UC-H-2.9的残余强度低于螺旋配筋较少的试件UC-H-2.0，UC-N-2.0，这是由于试件UC-H-2.9发生螺旋断裂的次数更多，导致试件整体强度下降地更加明显；当试件UC-O加载至峰值承载力后，内填混凝土的压溃导致试件轴压承载力迅速下降，曲线进入下降段；当试件的轴压承载力降至峰值承载力的70%时，轴压承载力的下降速率开始减缓；试件UC-O在方钢管竖向焊缝开裂前，其残余强度约为峰值承载力的50%，钢管竖向焊缝开裂时对应的轴向应变为1.85%.

综上可知，SCCFST试件的峰值承载力和CFST对比件基本相近，但SCCFST试件展现出明显优于CFST对比件的峰值后变形能力；随着螺旋箍筋的体积配箍率和屈服强度的提高，试件在螺旋箍筋第1次断裂的峰值后轴压性能越好.

2.2 试件破坏过程

以试件UC-N-2.0为例，其螺旋箍筋的应变发展曲线，如图5所示.图5中：ε2为横向应变；1st，2nd为螺旋箍筋中应变发展最早的两个应变片.由于试件中内填混凝土压溃区的位置不同，对应箍筋应变发展较快的区域也可能不同.由图5及相关计算可知:在试件加载至峰值承载力时，螺旋箍筋的应变发展较为缓慢，实测箍筋最大应变均低于7.0×10-4.对SCCFST试件而言，螺旋箍筋的应变发展存在一个拐点(大致为试件加载至峰值承载力开始下降时对应的试件轴向应变)，当箍筋应变发展至此拐点后，应变增长率大幅提高,并在较小的试件轴向应变区间内超过0.015.

SCCFST试件的螺旋箍筋在试验加载结束前均发生数次断裂(以试验中钢筋拉断发出的响声作为判断依据).高强螺旋箍筋第1次断裂时对应的轴向应变分别为1.42%,1.56%；相较于高强钢筋，普通钢筋的断后伸长率达到21.20%，然而，普通螺旋箍筋第1次断裂时对应的试件轴向应变为2.45%.这表明在普通螺旋箍筋断裂时，内填混凝土已发生严重的膨胀现象.内配高强螺旋箍筋试件每次箍筋断裂均导致轴向承载力的明显下降，且下降程度随螺旋箍筋体积配箍率的提高而增大.内配普通螺旋箍筋试件因箍筋断裂导致轴向承载力下降的现象并不明显.当试件UC-N-2.0加载至轴向应变为5%时，钢管竖向焊缝尚未开裂；试件UC-H-2.9的钢管竖向焊缝开裂时对应的试件轴向应变均超过4%；试件UC-O钢管竖向焊缝开裂时对应的试件轴向应变为1.85%.这是因为螺旋箍筋可有效地约束核心混凝土的膨胀，延缓钢管竖向焊缝过早达到极限拉应变.

在轴力作用下，混凝土会发生侧向膨胀，使螺旋箍筋处于持续拉伸的状态.螺旋箍筋与核心混凝土间的作用，如图6所示.图6中：f为混凝土强度；dcor为箍筋直径；fyt为钢管的极限强度；Ast为钢管的横截面积.螺旋箍筋的拉伸会对混凝土产生横向约束力，限制混凝土的侧向膨胀，进而减小混凝土与钢管之间的作用力，减小钢管的侧向膨胀，因此，可延缓钢管的焊缝开裂.

2.3 试件的最终破坏形态及特征点

由于试件UC-H-2.9的破坏形态没有特别现象，故仅展示试件UC-O，UC-N-2.0，UC-H-2.0的最终破坏形态，如图7所示.由图7可知：3个试件均出现混凝土压溃现象；SCCFST试件的螺旋箍筋约束区外部混凝土的破坏程度明显大于箍筋约束区内的混凝土，进一步证明螺旋箍筋能有效地约束核心混凝土；在混凝土严重压溃的区域，螺旋箍筋存在断裂处，验证此前加载过程中对箍筋断裂的判断；内填混凝土严重压溃处对应钢管局部屈曲最严重的部位.

参照文献[14]的CFST柱轴压承载力计算公式，以此预测SCCFST柱和CFST柱的轴压承载力计算值N0，有

(2)

(a) UC-O (b) UC-N-2.0 (c) UC-H-2.0图7 试件的最终破坏形态Fig.7 Final failure modes of specimens

试件的主要试验结果，如表3所示.表3中：Nm为轴压承载力实测值；Nm/N0为轴压承载力实测值与计算值的比值；εm为轴向峰值载荷对应的轴向应变；εb为局部屈曲开始时的轴向应变；εr为螺旋箍筋第1次破裂对应的轴向应变；εf为垂直焊缝断裂对应的轴向应变.

综上可知，内配螺旋箍筋对CFST柱的轴压承载力提高有限；Nm与N0的比值为0.96～1.04，这在研究的参数变化范围内[1-7]；式(2)可较好地预测SCCFT柱的轴压承载力.

表3 试件的主要试验结果Tab.3 Main test results of specimens

3 延性分析

3.1 延性指标

图8 基于能量法的延性分析Fig.8 Ductility analysis based on energy method

延性比是衡量延性的一个常用指标，其定义为强度下降到峰值承载力的85%时对应的位移与屈服位移的比值.然而，对于承载力过峰值点后迅速下降，但在下降段后期仍保持较高承载力的试件(类似情况常发生于约束混凝土柱中)，延性比的评价方法并不适用.为了克服延性比的不足，Foster等[15]提出了基于能量概念的延性指标.

基于能量法的延性分析，如图8所示.图8中：σc为混凝土应力；εy为屈服应变；点A，B，C对应的横坐标分别为εy，3.0εy，5.5εy.

延性指标I5为曲线OB，OA与横坐标轴之间的面积之比.Foster等[15]建议屈服应变εy取上升段中0.75scm对应应变的4/3倍，其中，scm为内填混凝土的峰值应力； 同理， 延性指标I10为曲线OC，OA与横坐标轴间的面积之比.根据试验现象， 当应变达到5.5εy时，大部分试件中的箍筋已经发生多次断裂，构件的轴压承载力出现明显的下降.为了减小箍筋断裂对构件延性造成的影响，采用I5进行钢管混凝土的延性分析.

常规的轴压试验无法直接得出内填混凝土和钢管各自承担的轴力，故I5的计算是基于试件轴力-应变曲线，而不是内填混凝土应力-应变曲线.

图9 I5与λs的拟合关系Fig.9 Fitting relationships between I5 and λs

3.2 延性指标-配箍特征值曲线

为了确定延性指标I5和配箍特征值λs的关系，根据GB 50010-2010《混凝土结构设计规范》[16]，给出配箍特征值λs的计算公式为

(3)

基于式(3)，拟合延性指标I5与配箍特征值λs的关系，如图9所示.由于有理方程能比线性方程更加合理地表现出I5与λs的关系，因此，采用有理方程进行回归分析,可得

(4)

通过MATLAB软件计算得到回归方程判定系数R2=0.930 1.一般认为，R2大于0.75，表示模型拟合度很好.因此，式(4)与试验数据吻合较好.

4 结论

文中研究了内配螺旋箍筋方钢管高强混凝土柱的轴压性能，对内填混凝土强度为112 MPa的3个SCCFST试件和1个CFST对比件进行单调轴压加载，主要参数为螺旋箍筋的体积配箍率和屈服强度.研究得出以下5个主要结论.

1) 对于无螺旋箍筋约束的CFST柱， 内填高强混凝土在峰值后阶段表现出较严重的脆性. SCCFST试件的轴向承载力与CFST试件相近.然而，与CFST试件相比，SCCFST试件的峰值后性能有显著的提高.随着螺旋箍筋的体积配箍率和屈服强度的增加，试件峰值后性能的提高幅度也会增加.

2) 螺旋箍筋的应变在试件加载初期发展较为缓慢，当试件加载至峰值点时，螺旋箍筋应变开始快速发展.在试件加载过程中，SCCFST试件中的螺旋箍筋均发生断裂现象.对于内配高强螺旋箍筋的试件，每一次螺旋筋的断裂均会导致试件承载力的显著下降，而且试件承载力下降的程度随内配螺旋箍筋的体积配箍率的增大而愈发明显.对于内配普通螺旋箍筋的试件，螺旋筋断裂引起的承载力下降程度较为轻微.

3) 螺旋箍筋有效限制了核心混凝土的侧向膨胀，延缓钢管竖向焊缝过早达到其极限拉应变.因此，SCCFST试件中钢管竖向焊缝的性能优于CFST试件.

4) 在研究参数的变化范围内，文献[14]给出的普通CFST柱的轴压承载力计算公式可较好地预测SCCFT柱的轴压承载力.

5) 公式(4)可通过配箍特征值较好地反映CFST和SCCFT试件延性的变化.