基于改进飞蛾扑火优化算法的PMSM矢量控制优化*

杜 涛， 曾国辉，黄 勃， 韦 钰

(上海工程技术大学 电子电气工程学院，上海 201620)

0 引 言

永磁同步电机(premanent magnet synchronous motor,PMSM)具有结构简单、体积小、质量轻、调速范围宽、功率因数高、易于散热与维护等显著优点，广泛应用于电动汽车、工业机器人、数控机床等领域[1～3]。目前，矢量控制是PMSM高性能控制中最成熟、最广泛的控制方式[4]。矢量控制通常采用磁通与转矩解耦的按转子磁场定向的转速电流双闭环的系统结构，涉及到转速外环，励磁电流内环，转矩电流内环三个PI控制器。但是传统的根据工程经验进行参数整定复杂、困难，且PMSM在运行过程中受到自身参数变化和外界干扰等因素影响，整定的PI参数对于交流伺服调速系统可能不是最优的[5,6]。

飞蛾扑火优化(moth to flame optimization,MFO)算法是2015年由澳大利亚Mirjalili S提出的一种新的模拟飞蛾飞行的自然启发式算法。MFO算法本质上是一种群体智能算法，与粒子群优化算法[7]、蚁群算法[8]、人工蜂群算法[9]等典型的群智能算法相比，具有搜索精度高、收敛速度快和全局搜索能力强等显著优点。

本文将MFO算法与传统PI控制结合，在此基础上，对飞蛾与火焰的更新机制进行了改进，并应用到PMSM的转速外环和电流内环的调节器中，实现比例—积分(proportio-nal-integral,PI)参数的自整定与优化，以达到电机的最优控制[10]。

1 三相PMSM的数学模型与矢量控制

在两相同步旋转坐标系下，建立PMSM的数学模型，其基本电压方程和磁链方程分别为

(1)

(2)

式中ud,uq为定子电压的直、交轴分量;Rs为定子绕组电阻;p为微分算子;ω为转子角速度。ψd,ψq为定子磁链的d,q轴分量;Ld,Lq为定子的d,q轴电感;id,iq为定子电流的d,q轴分量;ψf为永磁体磁链。

转矩方程和机械方程分别为

(3)

(4)

式中pn为电机的极对数,Te为电磁转矩,TL为负载转矩,J为转动惯量。

如图1所示为内嵌式PMSM采用id=0的控制策略的三相PMSM双闭环矢量控制框图，其中,转速外环ASR(automatic speed regulator)，转矩电流内环ATCR(automatic torque current regulator)和励磁电流内环AFCR(automatic field current regulator)均采用MFO算法对PI参数进行整定与优化。调制方法采用的是空间矢量脉宽调制。

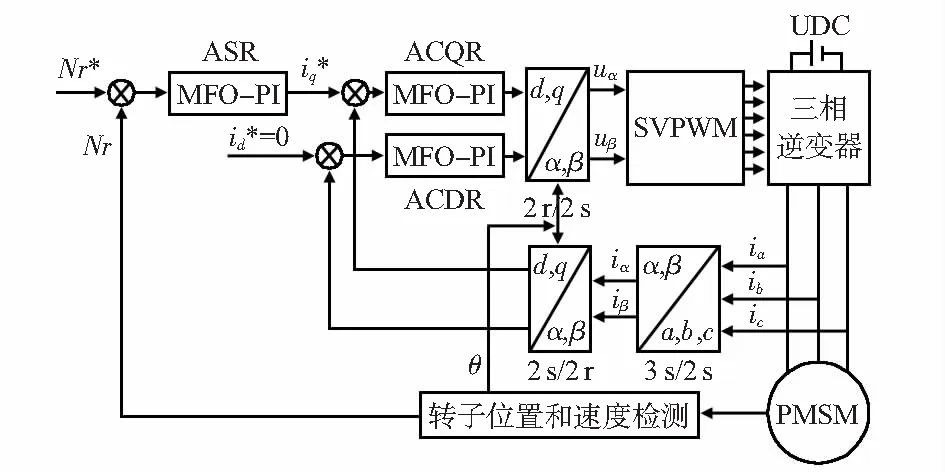
图1 三相PMSM双闭环矢量控制框图

2 MFO算法优化双闭环PI参数的实现

2.1 标准MFO算法

MFO算法的思想来源于飞蛾在夜间飞行时横向定位的导航机制。在这种导航机制下，飞蛾通过与月亮保持一个固定的夹角来飞行，由于月亮距离飞蛾非常远，所以在这种方式下能确保飞蛾沿直线飞行[11]。但现实世界中，存在很多人造光源，而人造光源与飞蛾的距离远小于月亮与飞蛾之间的距离，当飞蛾仍然试图与人造光源维持一个固定夹角飞行时，就会被误导而表现出螺旋式飞行轨迹。

在MFO算法中，M为飞蛾种群矩阵，OM为飞蛾的适应度值矩阵，F为火焰位置矩阵，OF为火焰适应度值矩阵如下

(5)

(6)

式中n为飞蛾的个数，d为所求变量的维数，飞蛾矩阵与火焰矩阵维度相同。

在迭代过程中，飞蛾和火焰更新位置的方式不同。飞蛾是在空间中移动的搜索个体来搜寻最优目标，火焰是目前为止所对应的飞蛾能够搜寻到的最优目标，并存储飞蛾搜寻到的当前最优值。

对飞蛾扑火行为进行建模，每只飞蛾相对火焰位置更新的方程为

Mi=S(Mi,Fj)

(7)

式中Mi为第i只飞蛾，Fj为第j个火焰，S为螺旋形函数。

模拟飞蛾路径更新机制选取的对数螺旋线如下

S(Mi,Fj)=Di·ebt·cos(2πt)+Fj

(8)

Di=|Fj-Mi|

(9)

式中Di为第i只飞蛾与第j个火焰之间的距离，b为对数螺旋线形状常数，t为[-1,1]间的随机数，它定义了飞蛾下一位置接近火焰的程度，如图2所示，t=1为飞蛾距离火焰最远的距离，t=-1为飞蛾最接近火焰的距离。

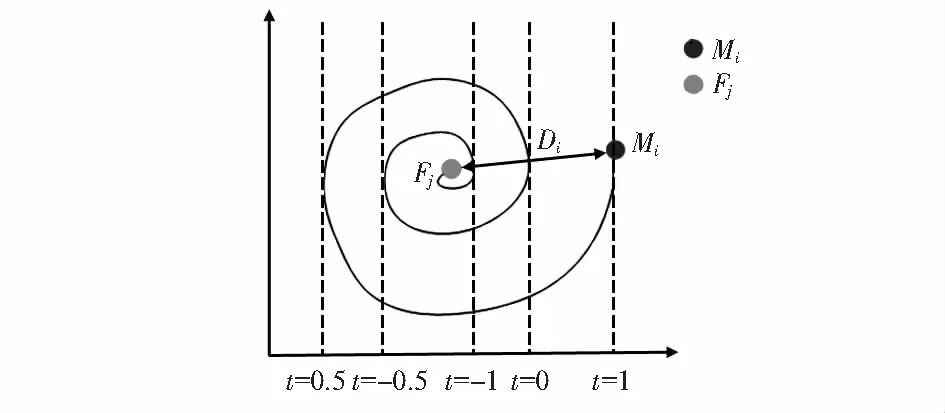
图2 飞蛾围绕火焰飞行的对数螺旋线轨迹

在式(8)中，每次的位置更新都是n只飞蛾朝向n个火焰移动，这样会使搜索的最佳空间位置陷入局部最优解。为了避免陷入局部最优解，在火焰位置更新后，火焰根据它们的适应度函数值由高到低排序，飞蛾的更新相对于火焰的排序。

为了提高MFO算法的收敛速度，火焰数量在更新迭代过程中自适应地减少，如式(10)所示

(10)

式中N为最大火焰数量，T为最大迭代次数，l为当前迭代次数。

2.2 改进的MFO算法

MFO算法具有飞蛾和火焰两个候选解，飞蛾通过在搜索空间中位置更新，逐渐逼近搜寻的火焰目标，飞蛾与火焰的更新机制对于搜索到最优解至关重要。因此，为了减小算法计算量，避免飞蛾搜寻最优解的过程陷入局部最优，对标准MFO算法的飞蛾与火焰更新机制进行了改进与优化。针对标准的MFO算法飞蛾位置更新采用的是参考按照适应度函数值由高到低排序的火焰，改进后的MFO算法更新机制是参考适应度函数值最优的火焰F1，提高了算法的搜索精度；对于火焰数量更新，采用收敛速度更快的曲线搜索代替标准MFO算法的直线搜索，提高了算法的收敛速度。相应的改进后的飞蛾位置更新与火焰数量更新公式分别如式(11)、式(12)所示

Mi=S(Mi,Fj)=Di·ebt·cos(2πt)+F1

(11)

flameno=round[T/(l+T/N)]

(12)

2.3 基于改进MFO算法的双闭环PI控制器设计

采用改进MFO-PI控制器的结构如图3所示，控制器主要分为两部分：一部分为虚线框所示的改进MFO算法，输入为闭环负反馈系统给定值与实际值的偏差，输出为对比例积分参数离线整定全局最优值；另一部分为传统的PI控制器。

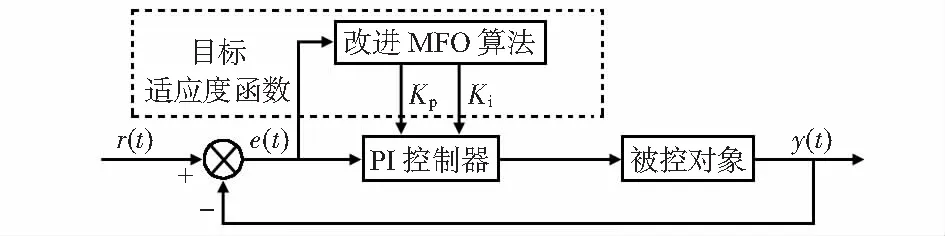
图3 改进MFO-PI控制器结构

用改进MFO算法对转速、电流双闭环控制的PI参数进行整定，即找出三个PI控制器的最优组合参数K

K=[Ksp,Ksi,Kqp,Kqi,Kdp,Kdi]

(13)

将待优化的6个参数看作飞蛾搜寻火焰的最优个体空间位置，飞蛾飞行在6维空间中搜寻6个参数的最优组合使系统的适应度函数值最低。为了使PMSM调速系统性能最优，等价转化为目标适应度函数寻找全局最优解。因此，目标适应度函数的选择对于系统的性能至关重要。本文采用误差性能指标积分时间和绝对误差(ITAE)加入超调惩罚项作为其适应度函数，以提高转速外环和电流内环的快速动态响应性能，减小超调量，提高抗干扰能力。相应的适应度函数如式(14)所示

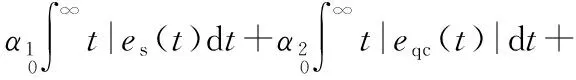
(14)

式中α1,α2,α3,β分别为转速外环ASR，转矩电流内环ATCR，励磁电流内环AFCR和转速超调量的惩罚权重，Mp为转速的超调量。

2.4 改进MFO算法实现步骤

采用改进飞蛾扑火优化算法优化PMSM调速系统的具体步骤如下:1)改进MFO算法的初始化,设置所需优化的3组PI参数的维度D，搜索范围[LB,UB]，飞蛾种群规模n，螺旋形状常数b，最大迭代次数N；2)确立目标适应度函数J，将PMSM调速系统性能最优，转化为目标适应度函数取得最小值Jmin；3)根据飞蛾所处的空间位置计算相应的自适应度值，将飞蛾搜寻到当前最优解的个体的空间位置赋值给火焰适应度矩阵OM;4)飞蛾的位置更新参考适应度函数值最优的火焰F1，如式(11)所示；5)将更新后的飞蛾与火焰位置按照适应度值进行排序，适应度值排序靠前的飞蛾个体所处空间位置更新为下一代火焰的位置；6)采用式(12)自适应地减少火焰数量；7)返回步骤(3)，进行下一次迭代更新，直至达到设置的最大迭代次数；8)输出搜寻到的最优飞蛾个体空间位置及相应的适应度函数值，即火焰的最终空间位置及适应度函数值，算法结束。

3 仿真实验验证

根据图1在MATLAB/SIMULINK环境中搭建了PMSM按转子磁场定向的矢量控制系统的仿真模型，对本文提出的改进MFO算法优化的PI控制器、标准MFO算法优化的PI控制和传统依据工程经验的PI控制器进行了对比实验，对三种方式的所得到的电机空载启动、变载、变速运行中的速度响应和转矩响应进行比较。首先，电机空载启动，给定转速为800 r/min，然后，0.2 s时给电机加10 N·m的负载，最后0.4 s电机加速运行到1 000 r/min。

本仿真实验中，飞蛾种群规模为n=10，最大迭代次数N=50，待求变量的维度D=6，待优化控制参数Ksp,Ksi的搜索范围为[0,10]，Kqp,Kqi,Kdp,Kdi的搜索范围均为[0,1 200]，螺旋形状常数b=1。适应度函数中的惩罚权值分别为α1=0.7,α2=0.5,α3=0.5,β=0.3。永磁同步电机和变换器的参数如表1所示。

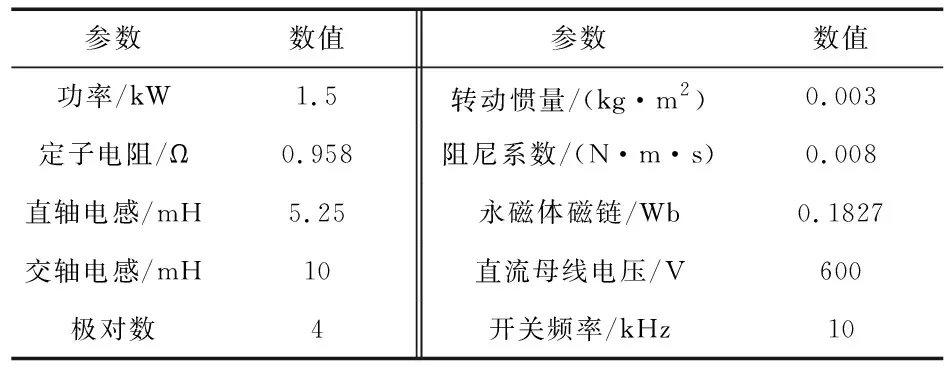
表1 永磁同步电机和变换器相关参数

如图4所示为本文提出的MFO算法的适应度函数值的收敛曲线，可以看出与标准MFO算法相比，改进MFO算法的搜索能力更强，搜索精度更高。两种算法初始阶段具有很快的下降性能，改进MFO算法经34次迭代后适应度函数收敛到最优值为Jmin=0.590 49，收敛速度和收敛精度均优于标准MFO算法，改进MFO算法得到的三个PI控制器的最优参数为：Ksp=1.874 6,Ksi=9.702 0,Kqp=169.442 6,Kqi=278.672 2,Kdp=73.788 3,Kdi=631.742 2。

图4 MFO算法适应度函数值的收敛曲线

由图5可以看出，相比于传统PI控制，采用标准MFO优化控制策略，电机在整个运行过程中，转速超调量明显减小，在变载、变速运行时，动态响应速度更快，调节时间缩短，且电机稳态时转速误差在5 r/min。采用改进MFO控制策略，电机启动过程的超调进一步减小，且电机稳态时转速误差在2 r/min，稳定性更好。

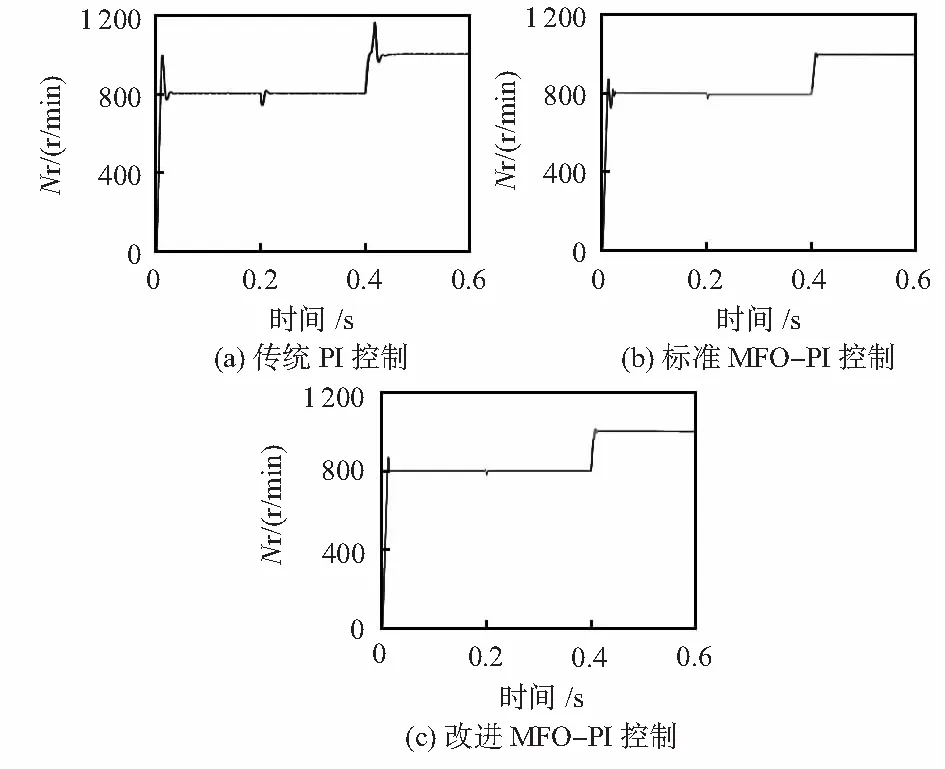
图5 PMSM转速特性曲线

如图6所示，与传统PI控制相比，标准MFO优化的PI控制器，最大超调量变小，转矩动态响应更快，但是开始启动时超调量较大，出现抖振现象。改进后的MFO算法，空载启动的动态过程转矩抖振变小，且调节时间缩短，变载、变速时动态响应速度快，总体的动静态性能较好。

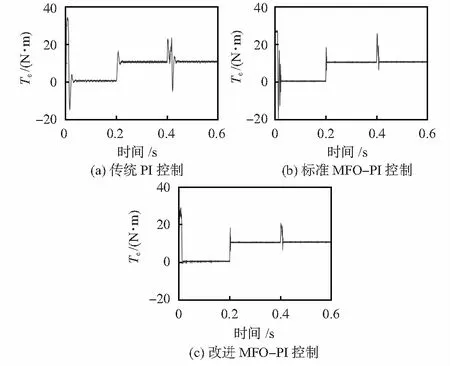
图6 PMSM电磁转矩特性曲线

4 结 论

本文采用MFO算法对PMSM矢量控制系统的3个PI控制器进行优化，并对飞蛾位置与火焰数量更新机制进行了改进，减小了传统人工调试PI参数的复杂性，缩短调节时间。将6个待优化的参数看作是飞蛾搜寻火焰最优个体所处的空间位置，通过构建合适的目标适应度函数，将永磁同步电机调速系统的性能最优，转化为目标函数求得最优解的问题。为了使电机跟踪转速效果较快，减小超调量，目标函数构建中加入超调惩罚项，较好地实现了PMSM的高性能控制。实验结果表明：采用改进后的MFO算法的PI参数整定方法，具有动态响应快，超调量小，鲁棒性好的优势，证明了优化策略的有效性。