基于RF-GRU风速预测的风电MPPT控制*

金俊喆， 武 鹏， 董祥祥， 葛传九， 陈 蓓

(上海工程技术大学 电子电气工程学院，上海 201620)

0 引 言

风能是一种重要的低碳能源，已被广泛用来发电[1]。然而，风力发电受风速变化影响较大。由于短期风速的随机性和非线性特性,使风速难以精确预测[2,3]。为最大限度利用风能，风电机组需采用最大功率点跟踪(maximum power point tracking,MPPT)控制，使风机出力可以跟踪风能，保持最大功率输出。

目前常用的MPPT控制算法有叶尖速比法、功率反馈法、爬山法[4]等。文献[4]比较了不同的MPPT算法的优缺点；文献[5]提出了变步长爬山法与模糊算法结合的算例，通过模糊算法追踪至最大功率点附近，再通过多等级变步长爬山法精确定位到最大功率点。在风速预测方面，文献[6]提出了通过改进条件极大似然估计法优化多重离群点平滑转换自回归模型参数，再以此模型进行风电功率估计；文献[7]提出了一种支持向量机与自适应原理结合的风速预测MPPT方法；文献[8]将风速预测与爬山法相结合，运用长短期记忆(long short term memory,LSTM)神经网络来预测风速，在此基础上调整爬山法的步长和方向来实现MPPT跟踪。上述方法在短期风速预测及风电MPPT追踪上都有着不错的效果，但其模型过于复杂，且风速的实际影响未能考虑其中。

为此，考虑到风速的实际影响及传感器所得数据的一定延迟性，本文提出了预测与追踪同步控制的精简策略。首先，运用随机森林(random forest,RF)算法寻找与风速相关度最高的变量进行变量降维，以此数据集构建门控循环单元(gated recurrent unit,GRU)神经网络,实现短期风速预测；然后，在短期风速预测的基础上，提出了改进的粒子群优化(improved particle swarm optimization,IPSO)算法；最后，利用MATLAB进行仿真，验证了本文方法的有效性。

1 风速预测模型

1.1 风机模型

根据贝兹理论可知,风机的机械功率与转速、桨距角、半径有如下关系[9]

(1)

λ=Rω/v

(2)

式中Pm为风机功率，ρ为空气密度，R为风轮半径，v,ω分别为风速和电机转速，λ为叶尖速比，Cp为最大风能捕获系数，是λ和ω的一个非线性函数[10]。 在桨距角一定时，存在着一个λ，使得Pm达到最大值[11]。由此可知，风电MPPT控制需要较准确的风速信息，才能进行叶尖速比的调节。而风速变化很快，周期性差，且传感器测得的风速具有一定的延迟性，所得数据不能进行实时MPPT，因此，可以采用预测风速的方法，实现实时MPPT。

1.2 RF-GRU的风速预测

1) 数据的降维处理

在风电场中，风速的变化与许多变量有关系，如果直接运用这些变量，会产生梯度消失的问题。RF法是一种集成学习方法，以决策树为基本单元，可计算标签与输入之间的关联程度大小。其先根据参数建立决策树，记为N，之后随机分配输入变量至每一颗决策树进行训练，完成之后，计算袋外误差记OB1，再随机加入干扰重复上述步骤，其袋外误差记OB2，根据式(3)计算变量对于标签贡献度G大小，进行贡献度排序，得出前4个贡献度最高的变量，记为{M1,M2,M3,M4}。运用此方法，可以使风速相关变量由20个变成4个

(3)

2)GRU网络的建立

GRU是一种改进的RNN，相对于另一种变形LSTM来说，GRU结构更加简单，运算快且不容易过度拟合[12]。GRU的单元内部结构如图1所示，其在LSTM的基础上，通过重新整合，组成了新的门控单元，分别称为更新门和重置门。重置门依据门控信号可以决定之前信息保留下来的程度，记忆最重要的信息，再传输进入更新门，更新门根据前者相关信息和门控信号进行信息更新，得到这一单元的输出结果。

图1 GRU网络内部结构

nt=sigmod(ωzxt+mzht-1)

(4)

rt=sigmod(ωrxt+mrht-1)

(5)

(6)

(7)

式中 sigmod为激励函数，将结果反馈至0～1之间，其表达式如式(8)所示。ωz,mz,ωr,mr为相应的权值矩阵。tanh为双曲正切激活函数，其表达式如式(9)所示

(8)

(9)

GRU风速预测流程图如图2所示。

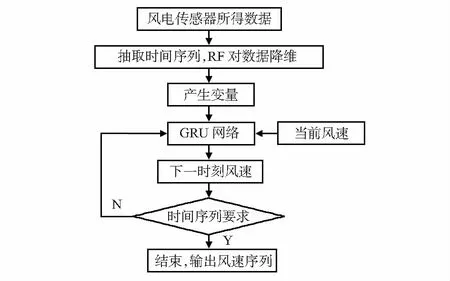
图2 GRU风速预测流程图

2 基于IPSO算法的风电MPPT控制

粒子群优化(PSO)算法可以通过粒子的飞翔在空间内进行搜索，在位置的更新变化下得到函数极值，从而实现MPPT控制。

2.1 粒子群算法原理

在粒子群算法中，粒子有两个属性：速度和位置。粒子之间通过各自的信息交流，更新自己的位置和速度，在误差范围内聚集至最大点处，即视为找到了最佳解[13]。其速度和位置更新如式(10),式(11)所示

(10)

(11)

式中k为迭代次数，ω为惯性权重，c1,c2为学习因子，r1，r2为[0,1]上的随机数，Pid为个体极值，Pgd为全局极值，Xid为粒子所在的位置，Vid为粒子速度。

粒子群算法在搜索过程中会出现速度过慢、全局搜索能力不足等问题。由式(10)可知，其更新速度由ω，c1，c2的大小决定。ω控制着全局搜索能力。ω越大，收敛速度较慢，但可以提高全局搜索能力；ω越小，收敛速度加快，但容易出现局部最优。c1，c2代表着粒子本身的信息和对外交流的信息[14]。

基于1.2节预测所得的风速信息，从粒子分布、权重等多个方面对粒子群参数进行优化，使其能满足风电功率曲线MPPT跟踪的要求。

2.2 改进的粒子群算法

1)粒子分布优化

图3(a)是风轮角速度与最大功率系数的关系图。

假定在t0时刻，风速为v0，此时搜索到的最佳转速记为ω0，取得的最大功率点记为A点，两端点分别记为O点和B点。在搜索的同时，预测网络已经预测到下一时刻，即t1时刻，设其预测风速为v1，由式(1),式(2)可知，若v1大于v0，则t1时刻搜索到的最大功率点在A点的右侧，在预测风速的基础上，可以将粒子分布在A点和B点之间。同时，B点的位置也可以根据式(12)进行移动，移动到的最终位置记为C。这样，通过上述步骤，搜索范围由O点至B点的大范围变成A点至C点的小区间，优化后的粒子分布如图3(b)所示。式(12)如下

(12)

式中Xt+1为C点位置，Xt为B点位置，vt+1为t1时刻预测风速，vt为t0时刻风速，m为调节系数。

图3 优化前后粒子分布

由图3(b)可知，区间的缩小使得每次的粒子分布更加紧凑，在此条件下只需增加粒子群的局部搜索能力即可粒子找到最优值，避免了粒子群全局搜索能力的不足及系统出现震荡。

2)种群规模调整

粒子群种群规模对于搜索速度有着一定影响，因此需要对种群进行调整，在风速变化平稳时，将粒子种群限制在20以内；在风速变化剧烈时，将粒子种群规模提升至50～80之间，其随着风速差值的变化而进行实时调整。

3)惯性权重、学习因子优化

惯性权重对搜索过程有着重要的影响。在搜索过程中，应保持高效的全局搜索能力，并且在搜索的后期，逐渐提高收敛速度。因此，ω应逐渐减小。其计算表达式如式(13)～式(15)所示

(13)

(14)

(15)

式中k为目前迭代次数，n为最大迭代次数，随着迭代次数的增加，ω呈指数衰减。在搜索的后期，当最后三次搜索结果的方差不大于0.4，说明已找到最大功率点，终止搜索过程。因此，ω可以在后期稳定在一个较小数值下，增加局部搜索能力，防止系统在最大功率点处振荡。基于RF-GRU风速预测的改进粒子群算法总流程图如图4所示。

图4 基于RF-GRU风速预测的改进粒子群算法总流程图

3 仿真实现

采用MATLAB 2018a软件对该策略进行仿真，以ODE23算法对模型求解，步长随着模型的求解过程而实时改变。仿真过程中，先验证风速预测精度，再通过RF-GRU模型预测风速后进行MPPT控制。仿真时长设为2 s，初始风速为8 m/s，在0.3～1 s时间内风速发生改变：0.3 s时风速变为12 m/s;0.6 s时风速变为16 m/s;0.8 s时风速下降为14 m/s。

3.1 风速预测模型仿真

风机模型参数：切入风速为5 m/s，切出风速为18 m/s，桨距角为0°，风轮半径为6 m，Cp理论最大值为0.48。

在风速预测训练网络过程中，选取了某风电场1月内的风速数据及相关变量，运用RF提取出特征变量，构建GRU模型训练，共选取3 000组数据，其中选择80%进行训练，选择200组数据作为测试数据，其预测风速误差如图5所示。

图5 风速预测误差结果

由图5可知，GRU预测所得风速最大误差在0.1左右，并经多次仿真得均方差为0.23，符合预测的精度，表明RF-GRU预测所得风速可用于之后的MPPT控制。

3.2 粒子群MPPT算法结果

通过风速预测模型，在风速变化的基础上，以改进的的粒子群进行MPPT控制，其参数设置：种群规模M=25，最大迭代次数N=30，初始值ω=0.8，c1=c2=3.5。Cp变化过程如图6所示。

图6 粒子群风电MPPT仿真结果比较

由图6可知，在风速突变时，传统的粒子群会因重新搜索，造成Cp大幅滑落；而基于风速预测的粒子群算法由于预测了下一时刻的风速，从而可以进行更平滑的搜索，不会造成风电系统振荡。

基于以上数据可知

1)RF-GRU可以较为准确预测风速，为后面粒子群优化提供理论依据。

2)基于风速预测的优化粒子群算法由于粒子群的粒子分布边界的限制及惯性权重的实时改变可以更快、更平滑地找到最大功率点，避免了风电系统振荡的情况，可以很好实现风电MPPT。

4 结 论

对于传统的风电MPPT控制策略，本文提出一种基于RF-GRU风速预测的改进粒子群MPPT控制策略。首先，通过一个风电场的历史数据，使用RF法进行特征提取，建立GRU进行输入输出数据的拟合训练，通过前一时刻预测了下一时刻的风速；然后，运用该风速信息，确定粒子分布情况和种群规模，再调整粒子群算法的惯性权重和学习因子，增加其搜索速度和精度；最后，通过MATLAB仿真验证了所提策略的正确性和有效性。